Calculus AB Unit 5 Review: Particle Motion
TLDRThis video script offers a comprehensive review of a physics problem set, focusing on the motion of particles along the x-axis. It covers concepts such as initial position, time at the origin, average velocity, speed, and direction changes. The script uses mathematical equations and graphs to explain how to determine when a particle is at rest, moving left or right, and when it changes direction or experiences varying speeds. It also applies the mean value theorem to real-world scenarios like speeding violations, providing a practical understanding of calculus concepts.
Takeaways
- 📚 The script covers a unit 5 review problem involving a particle's motion along the x-axis, described by the position function X(T) = T^3 - 12T + 5.
- 🏁 The initial position of the particle is determined to be 5 units, found by evaluating X(0).
- 🔍 The particle's position at the origin is calculated by solving the equation T^3 - 12T + 5 = 0, yielding two time points, T ≈ 0.43 and T ≈ 3.23.
- ⏱ The average velocity of the particle over the interval from T=1 to T=4 is determined to be 9 units.
- 📈 The speed of the particle at T=4 is found to be increasing, as both velocity and acceleration are positive at this time.
- 🔄 The particle changes direction at T=2, identified by the velocity passing through zero and changing sign from negative to positive.
- 🚫 The particle is moving to the left on the interval from T=0 to T=2, where the velocity is negative.
- 📏 The total distance traveled by the particle over the interval from T=1 to T=4 is calculated to be 37 units.
- 📉 The script also discusses the velocities of a rocket at specific times, including intervals where velocity is zero and where the rocket's position is decreasing.
- 📊 An approximation for the rocket's acceleration at T=5 is given, using the average rate of change between the surrounding points.
- 🔢 The script explains the use of the intermediate value theorem to determine intervals where the velocity of an object is zero, assuming continuity.
- 📘 The mean-value theorem is applied to verify certain conditions and to find values where the derivative of a function equals the average rate of change over an interval.
Q & A
What is the initial position of the particle moving along the x-axis as described in the script?
-The initial position of the particle is 5 units, determined by substituting T = 0 into the position function X(T) = T^3 - 12T + 5.
When is the particle at the origin according to the given position equation?
-The particle is at the origin at two times: T = 0.43 and T = 3.23, found by solving the equation T^3 - 12T + 5 = 0.
What is the average velocity of the particle over the time interval from 1 to 4?
-The average velocity over the time interval from 1 to 4 is 9 units, calculated as (X(4) - X(1)) / (4 - 1), where X(T) is the position function.
Is the speed of the particle increasing or decreasing at time T equals 4?
-The speed of the particle is increasing at time T equals 4, as both the velocity and acceleration at this time are positive.
When does the particle change direction according to the velocity equation?
-The particle changes direction at T equals 2, as this is when the velocity changes sign from negative to positive.
In what time interval is the particle moving to the left?
-The particle is moving to the left on the interval from 0 to 2, as the velocity is negative in this interval.
How is the total distance traveled by the particle over the time interval from 1 to 4 calculated?
-The total distance traveled is calculated by finding the absolute value of the change in position from 1 to 2 and from 2 to 4, summing up to 37 units.
Is there an interval during which the rocket's velocity is 0 based on the provided data?
-Yes, assuming the velocity function is continuous, there must be an interval between 12 and 14 seconds where the velocity is 0, as it changes from 2 to -3.
During which time interval is the rocket's position decreasing?
-The rocket's position is decreasing on the interval from 14 to 25 seconds, based on the negative velocity values in the provided data.
How can you estimate the acceleration of the rocket at T equals 5 using the given data?
-The acceleration at T equals 5 can be estimated by calculating the average rate of change of velocity between T = 4 and T = 6, resulting in an acceleration of -1 feet per second squared.
What are the conditions for the mean value theorem to be applicable to a function on a given interval?
-The mean value theorem is applicable if the function is continuous on the closed interval and differentiable on the open interval within that range.
How can you determine if a function has a relative extreme point at a certain value?
-A function has a relative extreme point at a certain value if the derivative shows a sign change around that value, indicating a change from increasing to decreasing or vice versa.
What is the justification for the trucker being cited for speeding based on the mean value theorem?
-The trucker was cited for speeding because the mean value theorem guarantees that at some point during the trip, the trucker's instantaneous speed was equal to the average speed of 79.5 miles per hour, which exceeds the speed limit.
How can you sketch a graph of a function with given characteristics such as increasing, decreasing, concave up, and concave down?
-You can sketch the graph by marking the known points, indicating the direction of the function (increasing or decreasing), and the concavity (concave up or down) between intervals, ensuring the graph reflects the given properties at each point.
Outlines
📚 Particle Motion Analysis
This paragraph discusses the initial position and motion of a particle moving along the x-axis. The position function X(T) is given by T^3 - 12T + 5, and the initial position is determined to be 5 units at T=0. The particle's position at the origin is found by solving X(T)=0, yielding two times T=0.42 and T=3.23. The average velocity over the interval from T=1 to T=4 is calculated to be 9 units. At T=4, the particle's speed is analyzed by comparing velocity and acceleration, concluding it is increasing due to both being positive at this time.
🔄 Direction Change and Distance Calculation
The paragraph explores when the particle changes direction by examining the velocity function, which is derived from the position function. It is determined that the particle changes direction at T=2, as the velocity changes sign from negative to positive. The interval where the particle moves to the left is identified as T being greater than or equal to 0 and less than 2. The total distance traveled over the interval from T=1 to T=4 is calculated by splitting the interval at the point of direction change and summing the absolute changes in position, resulting in a total distance of 37 units.
🚀 Rocket Velocity Analysis
This section analyzes the velocity of a rocket at specific times. It is deduced that there must be an interval where the velocity is 0 based on the intermediate value theorem, given the continuous nature of the velocity function and the recorded velocities. The rocket's position is noted to decrease when the velocity is negative, specifically between T=14 and T=25. An approximation for the rocket's acceleration at T=5 is calculated using the average rate of change, resulting in an acceleration of -1 feet per second squared.
📉 Rocket Motion and Acceleration Estimation
The paragraph calculates the rocket's average acceleration over the interval from T=0 to T=12 using the change in velocity over time, resulting in an average acceleration of -13 feet per second squared. It also discusses the speed and acceleration of a particle at T=5, concluding that the speed is decreasing due to the velocity and acceleration having opposite signs. Fundamental concepts of motion, such as rest, direction change, constant velocity, and increasing or decreasing velocity, are explained in relation to their effects on position.
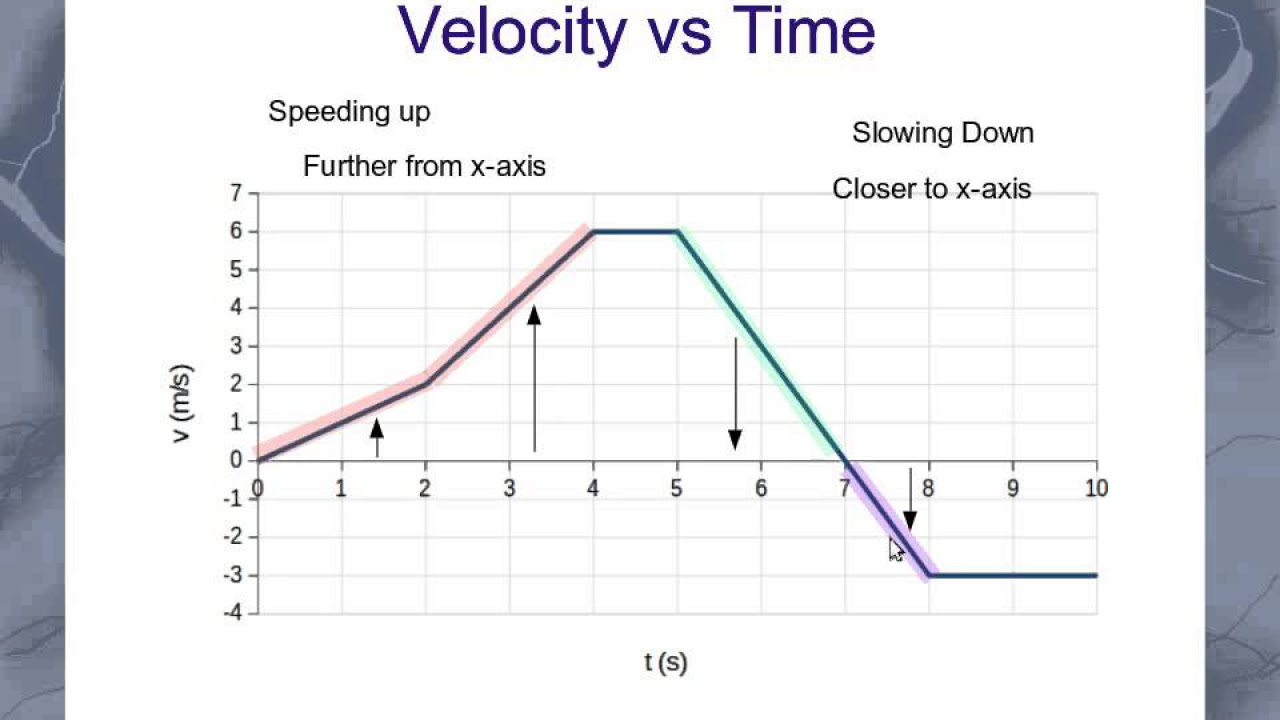
📈 Velocity and Acceleration Graph Interpretation
The paragraph interprets a velocity graph to determine the particle's motion. It identifies when the particle is moving left or right based on the sign of the velocity and when the particle is at rest when the velocity is zero. The time when the particle changes direction is found to be at T=9, where the velocity changes sign. The greatest speed of the particle is determined to be at T=15 with a speed of 6 units, and the acceleration at T=1 is calculated using the slope of the velocity graph, resulting in an acceleration of 1.5 units.
📊 Mean Value Theorem Application
This section verifies the conditions of the mean value theorem for a given function and finds a value C that satisfies the theorem's conclusion. The function is continuous on the closed interval from 0 to 3 and differentiable on the open interval, satisfying the theorem's conditions. The derivative of the function is set equal to the average rate of change, and the value of C is found to be 0.897, confirming the theorem's application.
🔍 Function Continuity and Differentiability
The paragraph examines the continuity and differentiability of a function on the interval from 1 to 4. The function is continuous and differentiable everywhere on this interval, except at x=-2, which is outside the interval of interest. The mean value theorem is confirmed to apply, guaranteeing a value C within the interval where the derivative equals the average rate of change, and this value is found to be 2.43.
📌 Checking Mean Value Theorem Hypotheses
The paragraph checks the hypotheses of the mean value theorem for a piecewise function. The function is continuous on the closed interval from 0 to 2 and differentiable on the open interval, with the exception of x=1, where the function has a discontinuity. The conditions for the mean value theorem to apply are discussed, including the need for the function to be continuous at endpoints and differentiable on the interval, leading to the determination of specific values for a, M, and B that satisfy these conditions.
🚚 Mean Value Theorem in Real-World Scenario
This section applies the mean value theorem to a real-world scenario involving a trucker who was cited for speeding. The trucker's average speed over a two-hour period is calculated, and the mean value theorem is used to justify that the trucker must have been driving at the average speed of 79.5 miles per hour at some point during the trip, which exceeds the speed limit.
📊 Identifying Relative Extremes
The paragraph uses the first derivative test to identify relative extreme points of a function that is continuous and twice differentiable except at x=1. A relative minimum is found at x=1 due to a sign change in the derivative. The maximum value of the function on the interval from -1 to 4 is determined by evaluating the function at its relative extreme point and at the endpoints, concluding that the maximum value is 3 at x=4.
🖌️ Sketching a Function with Given Characteristics
The final paragraph describes the process of sketching a function with specific characteristics based on the given information about its derivatives. Key points are plotted, and the function's behavior between these points is described, including whether it is increasing or decreasing and concave up or down. The sketch includes a cusp at x=1 and attempts to reflect the slopes indicated by the derivative at various points.
Mindmap
Keywords
💡Initial Position
💡Origin
💡Average Velocity
💡Speed Increasing or Decreasing
💡Direction Change
💡Moving Left
💡Total Distance Traveled
💡Intermediate Value Theorem
💡Average Acceleration
💡Mean Value Theorem
Highlights
The initial position of a particle moving along the x-axis is determined to be 5 units, derived from the position function X(T) at T=0.
The particle's position is zero at two distinct times, approximately T=0.43 and T=3.23, indicating it is at the origin at these instances.
The average velocity of the particle between time T=1 and T=4 is calculated to be 9 units, using the position function and the definition of average velocity.
At time T=4, the speed of the particle is found to be increasing, as both velocity and acceleration are positive.
The particle changes direction at T=2, identified by the velocity function changing sign from negative to positive.
The particle is moving to the left on the interval from T=0 to T=2, deduced from the negative velocity values on this interval.
The total distance traveled by the particle between T=1 and T=4 is 37 units, calculated by summing the absolute changes in position over sub-intervals.
An interval is identified where the rocket's velocity is 0, applying the intermediate value theorem to the given velocity values.
The rocket's position is found to be decreasing on the interval from T=14 to T=25, based on the negative velocity values.
An approximation for the rocket's acceleration at T=5 is calculated using the average rate of change method.
The average acceleration of the rocket from T=0 to T=12 is determined, considering the change in velocity over this interval.
The speed of a particle is found to be decreasing at T=5, as the velocity is positive but decreasing, indicating negative acceleration.
A piecewise function is analyzed for continuity and differentiability to satisfy the mean value theorem's conditions.
The mean value theorem is applied to a trucker's speed, justifying a speeding ticket issued for traveling an average speed exceeding the speed limit.
A function F is analyzed for relative extreme points between X=-1 and X=4, identifying a relative minimum at X=1.
The maximum value of function F is determined by evaluating its values at relative extreme points and endpoints.
A graph of function F is sketched, incorporating all given characteristics such as increasing/decreasing nature and concavity.
Transcripts
Browse More Related Video

Calculus AB Homework 5.5: Particle Motion Practice

Rectilinear Motion or Particle Motion or Straight Line Motion!

Calculus - Position Average Velocity Acceleration - Distance & Displacement - Derivatives & Limits

2017 AP Calculus AB Free Response #5

Calculus AB Homework 5.3: Position, Velocity, Acceleration
Interpreting Velocity graphs
5.0 / 5 (0 votes)
Thanks for rating: