Calculus Prerequisite Skills (Summer Packet) Part 3 of 3

Michelle Krummel

5 Aug 201742:47

EducationalLearning

32 Likes 10 Comments

TLDRThis video script serves as a comprehensive guide to prerequisite skills for success in calculus, focusing on simplifying rational exponents, exponential and logarithmic functions, and trigonometry. It covers topics like dividing numbers with the same base, factoring out terms, and combining like terms, while also explaining how to solve equations involving natural logarithms and exponential functions. The script also reviews basic trigonometry, including unit circle values, inverse trigonometric functions, and trigonometric identities, providing a solid foundation for tackling calculus problems.

Takeaways

📚 The video is a comprehensive guide on prerequisite skills for success in calculus, covering topics like simplifying rational exponents, exponential and logarithmic functions, and trigonometry.
🧭 The presenter, Michele Crummell, demonstrates how to simplify rational exponents by separating expressions into fractions and using the properties of exponents to simplify them.
🔍 Michele explains the process of simplifying complex expressions involving exponential functions by factoring out common bases and combining like terms.
📉 In the context of logarithmic functions, the video shows how to solve equations by setting the numerator to zero and factoring out common terms.
📈 The video includes examples of working with the natural logarithm, such as finding the value of 'k' in an exponential equation and simplifying logarithmic expressions.
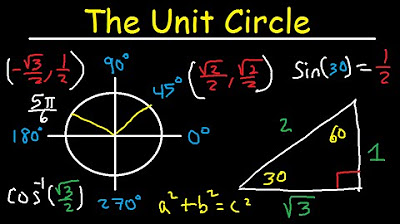
📚 Michele emphasizes the importance of understanding the unit circle and memorizing key values for solving trigonometric equations in calculus.
📐 The script reviews basic trigonometry, including the use of reference angles and the process of finding trigonometric values for various angles on the unit circle.
🔢 The video explains the use of inverse trigonometric functions, such as arcsine, arccosine, and arctan, and their respective domains and ranges.
📉 Trigonometric identities, including Pythagorean identities and even-odd properties, are discussed to show their application in calculus problems.
🔄 The presenter demonstrates the use of double angle formulas and power reducing formulas in solving trigonometric equations.
📝 The final part of the script involves solving specific trigonometric equations and simplifying expressions using substitution and trigonometric identities.

Q & A

What is the main topic of the video?
-The main topic of the video is the prerequisite skills needed for success in calculus, focusing on simplifying rational exponents, working with exponential and logarithmic functions, and trigonometry.
How does the video approach simplifying the expression x^2 - x / x^(1/2)?
-The video suggests separating the expression into two fractions, simplifying each fraction by subtracting exponents, and then combining them back together, eventually converting to radical form if necessary.
What is the process for simplifying the expression X^(1/2) * (8X^3 - X^4 + 3) / X?
-The process involves factoring out X^(-1/2), simplifying by subtracting exponents, combining like terms, and then rewriting the expression without a negative exponent by using the properties of exponents.
How does the video solve the equation involving e^(-x) * (2 + x) + e^(-x + x) = 0?
-The video sets the numerator equal to zero, factors out common terms, and then uses the properties of exponents to simplify and solve for x, considering the domain restrictions of the functions involved.
What is the solution for the equation 100 = 24 * e^(5k)?
-The solution involves dividing both sides by 24, isolating e^(5k), taking the natural logarithm of both sides, and then solving for k by dividing by 5.
How does the video explain the process of finding the value of G(e^2) if G(x) = ln(x) + sqrt(x)?
-The video substitutes e^2 into the function G(x), uses the properties of logarithms and square roots to simplify, and finds the value of G(e^2) as the sum of ln(e^2) and sqrt(e^2).
What are the key trigonometry concepts reviewed in the video?
-The key trigonometry concepts reviewed include understanding the unit circle, memorizing special angles, using reference angles for other quadrants, and knowing the domain and range of trigonometric functions.
How does the video explain the use of inverse trigonometric functions?
-The video explains that inverse trigonometric functions, such as arcsine, arccosine, and arctan, give the angle when given the ratio, and emphasizes the importance of understanding their domain and range.
What is the significance of the unit circle in trigonometry as explained in the video?
-The unit circle is significant because it provides the foundation for understanding trigonometric values at specific angles, and the video explains how to use memorized values and reference angles to find other trigonometric values.
How does the video handle the simplification of trigonometric expressions involving radicals?
-The video demonstrates the substitution of trigonometric identities into radical expressions, simplification by factoring, and the use of trigonometric identities to rewrite the expressions in a more simplified form.

Outlines

00:00

📚 Simplifying Rational Exponents and Functions

Michele Crummell discusses simplifying rational exponents, working with exponential, logarithmic, and trigonometric functions in the context of prerequisite skills for calculus. The explanation covers simplifying expressions like x squared minus x over the square root of x, converting to radical form, and subtracting exponents. It also touches on factoring out terms and combining like terms in expressions involving x and exponential functions.

05:05

🔍 Solving Exponential and Logarithmic Equations

This section delves into solving equations involving exponentials and logarithms. Michele demonstrates how to simplify expressions with e to the power of x and how to solve for x in equations where the numerator equals zero. The process involves factoring, using properties of exponents, and applying logarithms to isolate variables. The explanation also includes solving for x in equations involving e to the x plus constants.

10:05

📉 Applying Trigonometry and Inverse Functions

The focus shifts to trigonometry, emphasizing the importance of unit circle values for solving trigonometric equations in calculus. Michele explains how to use memorized values for sine and cosine at specific angles to determine other values, using reference angles to find sine, cosine, and tangent in different quadrants. The explanation also covers the process of finding angles using inverse trigonometric functions like arcsine, arccosine, and arctan, considering their domains and ranges.

15:08

📐 Understanding Trigonometric Identities and Solving Trigonometric Equations

This part reviews essential trigonometric identities, including Pythagorean identities and even-odd properties of trigonometric functions. Michele also discusses double angle formulas and power reducing formulas, providing examples of solving trigonometric equations using these identities. The summary includes finding angles that correspond to specific cosine values and understanding the implications of these values on the unit circle.

20:08

🔢 Solving Complex Trigonometric Equations

The script continues with solving more complex trigonometric equations, such as those involving tangent squared terms. Michele illustrates the process of isolating trigonometric terms, factoring, and using inverse trigonometric functions to find the solutions for x. The explanation cautions against dividing by zero and emphasizes the importance of considering all possible solutions, including those outside the principal period of the function.

25:10

📝 Substitution and Simplification in Trigonometric Expressions

The final part of the script reviews substitution techniques in trigonometric expressions. Michele demonstrates how to substitute u with expressions involving sine and tangent, simplifying radical expressions by recognizing perfect squares and applying trigonometric identities. The summary highlights the importance of considering the domain of the original expressions to ensure the solutions are valid within the specified constraints.

Mindmap

Keywords

💡Rational Exponents

Rational exponents are a way of expressing roots and fractional powers of a number. In the context of the video, simplifying rational exponents is a prerequisite skill for success in calculus. For example, the script mentions simplifying 'x squared minus x over X to the power one-half' by separating the expression into two fractions and then using the properties of exponents to simplify further.

💡Exponential Functions

Exponential functions are mathematical functions where the variable is in the exponent. They are fundamental in calculus for modeling growth and decay processes. The script discusses working with exponential functions, such as simplifying expressions involving 'X to the 1/2 times 8x cubed minus X to the fourth plus three'.

💡Logarithmic Functions

Logarithmic functions are the inverse of exponential functions and are used to solve for unknown exponents. They are crucial in calculus for solving equations that involve products and quotients of exponential terms. The video script includes an example of simplifying an expression with logarithms, such as 'X to the negative 1/2 over X'.

💡Trigonometry

Trigonometry is the study of the relationships between the angles and sides of triangles, particularly right-angled triangles. It is essential in calculus for solving problems involving periodic functions and understanding the geometry of space. The script covers basic trigonometry skills, such as understanding unit circle values, which are necessary for solving trigonometric equations in calculus.

💡Unit Circle

The unit circle is a circle with a radius of one, centered at the origin of a coordinate system. It is fundamental in trigonometry and calculus for determining the values of sine, cosine, and tangent at various angles. The script emphasizes the importance of knowing unit circle values for success in calculus, especially for solving trigonometric equations.

💡Arcsine

The arcsine function, written as sin^(-1) or arcsin, is the inverse of the sine function and returns the angle whose sine is a given number. It is used in the script to find angles when the sine value is known, such as in the problem 'arc sine of 0', which equals 0 because the sine of 0 is 0.

💡Arccosine

The arccosine function, written as cos^(-1) or arccos, is the inverse of the cosine function and finds the angle for a given cosine value. It has a range between 0 and π, providing angles in quadrants 1 and 2. The script uses arccosine to solve for angles in problems like 'arc cosine of 1/2', which equals π/3.

💡Arctangent

The arctangent function, written as tan^(-1) or arctan, is the inverse of the tangent function and is used to find an angle given the tangent of that angle. It has a range from -π/2 to π/2, covering quadrants 1 and 4. The script discusses arctangent in the context of finding angles for given tangent values, such as 'arctan of root 3', which equals π/3.

💡Trigonometric Identities

Trigonometric identities are equations that hold true for all values of the variable and are used to simplify trigonometric expressions. The script reviews several identities, such as the Pythagorean identity 'sine squared X plus cosine squared X equals 1', which is fundamental for solving trigonometric equations in calculus.

💡Double Angle Formulas

Double angle formulas are used to express the sine or cosine of double an angle in terms of the sine and cosine of the original angle. The script mentions these formulas in the context of simplifying expressions like 'sine of two theta equals two sine theta cosine theta', which is essential for solving problems involving angles that are multiples of the original angle.

Highlights

Simplifying rational exponents is a key skill for success in calculus, demonstrated through the expression x^2 - x/√x.

Exponential and logarithmic functions are essential, with examples given on simplifying expressions involving x^(1/2) and 8x^3 - x^4 + 3.

Trigonometry is fundamental in calculus, with the unit circle and special angles being crucial for solving trigonometric equations.

The process of simplifying expressions with e^(-x) and working with exponential functions is detailed, showcasing the application of exponent rules.

Binomial expansion of (e^x)^2 is explained, highlighting the use of exponent multiplication in simplifying complex expressions.

Solving equations involving e^x requires understanding the properties of exponential functions and their graphs.

The natural log function is applied to solve for y in logarithmic equations, demonstrating the inverse relationship with exponentials.

Finding the exact value of K in exponential equations involves using logarithms to isolate the variable.

Simplifying logarithmic expressions using properties like the power rule is explained, making complex problems more manageable.

The importance of memorizing unit circle values for quick trigonometric problem-solving is emphasized.

Mental strategies for recalling unit circle values without memorizing the entire circle are shared, providing an alternative approach.

The concept of reference angles and their use in finding trigonometric values for any angle is explained.

The process of finding the domain and range of inverse trigonometric functions such as arcsine, arccosine, and arctan is detailed.

Trigonometric identities, including Pythagorean identities, are reviewed, which are vital for solving advanced calculus problems.

Even-odd properties of trigonometric functions are outlined, aiding in understanding their behavior under input transformations.

Double angle formulas are presented, offering multiple ways to express these relationships for versatile problem-solving.

Solving trigonometric equations using identities and the unit circle is demonstrated, with a focus on finding exact solutions.

The application of power reducing formulas in simplifying trigonometric expressions is shown, streamlining complex calculations.

Substitution methods in simplifying radical expressions involving trigonometric functions are explained, highlighting algebraic manipulation.

Transcripts

Browse More Related Video

PreCalculus Midterm Exam Review

Basic Differentiation Rules For Derivatives

Indefinite Integral - Basic Integration Rules, Problems, Formulas, Trig Functions, Calculus

Unit Circle Trigonometry - Sin Cos Tan - Radians & Degrees

Rational Expressions Review

Logarithms Explained Rules & Properties, Condense, Expand, Graphing & Solving Equations Introduction

Related Tags

Calculus Skills Rational Exponents Exponential Functions Logarithmic Functions Trigonometry Guide Simplify Expressions Unit Circle Inverse Trigonometry Mathematics Tutorial Educational Content