Logarithms Explained Rules & Properties, Condense, Expand, Graphing & Solving Equations Introduction
TLDRThis video delves into the world of logarithms, explaining how to evaluate logs, apply the change of base formula, expand and condense logs, solve equations, and graph logarithmic functions. It covers properties of logs, such as combining and simplifying log expressions, and addresses the domain and range of both exponential and logarithmic functions. The video also demonstrates how to find the inverse function of a logarithmic function and how to graph these functions, highlighting the symmetry between exponential and logarithmic functions.
Takeaways
- 📝 Logarithms are used to evaluate expressions by finding the power to which a base must be raised to obtain a given number.
- 🔄 The change of base formula allows converting logarithms with different bases using the formula: log_b(A) = log_A / log_b.
- 📈 Logarithmic functions can be expanded and condensed using properties such as log(A*B) = log(A) + log(B) and log(A/B) = log(A) - log(B).
- 🌐 The domain of a logarithmic function is the set of all x values greater than a specific number, determined by the vertical asymptote.
- 📊 The range of a logarithmic function is all real numbers, from negative infinity to positive infinity.
- 🔢 Solving logarithmic equations often involves converting them to exponential form or using properties to isolate and solve for the variable.
- 🏠 The inverse of a logarithmic function is an exponential function, and vice versa, as they are symmetrical about the line y=x.
- 📌 When graphing exponential functions, the horizontal asymptote is used as a starting point, and the graph increases or decreases based on the exponent's sign.
- 🔍 To find the domain of an exponential function, set the exponent to zero and solve for x, then consider the restrictions based on the function's base.
- 🤔 Negative numbers and zero inside a logarithm are not allowed, as the logarithm of a negative number or zero does not exist.
- 📐 The properties of logarithms can be used to simplify expressions, such as combining logs with the same base into a single log or moving exponents inside logs to the front.
Q & A
How do you evaluate a logarithm?
-To evaluate a logarithm, you need to determine the power to which the base must be raised to obtain the given number. For example, to evaluate log base 2 of 4, you ask yourself '2 to what power gives me 4?' Since 2 times 2 is 4, the answer is 2 (log base 2 of 4 = 2).
What is the change of base formula for logarithms?
-The change of base formula for logarithms states that log base a of B is equal to log base B over log a. This allows you to change the base of a logarithm to any other number, including the natural logarithm base e.
How can you expand a logarithmic expression into multiple logs?
-You can expand a logarithmic expression by using the properties of logs. For example, log(base, a*b) can be expanded into log(base, a) + log(base, b). Similarly, log(base, a/b) can be written as log(base, a) - log(base, b).
What is the domain of a logarithmic function?
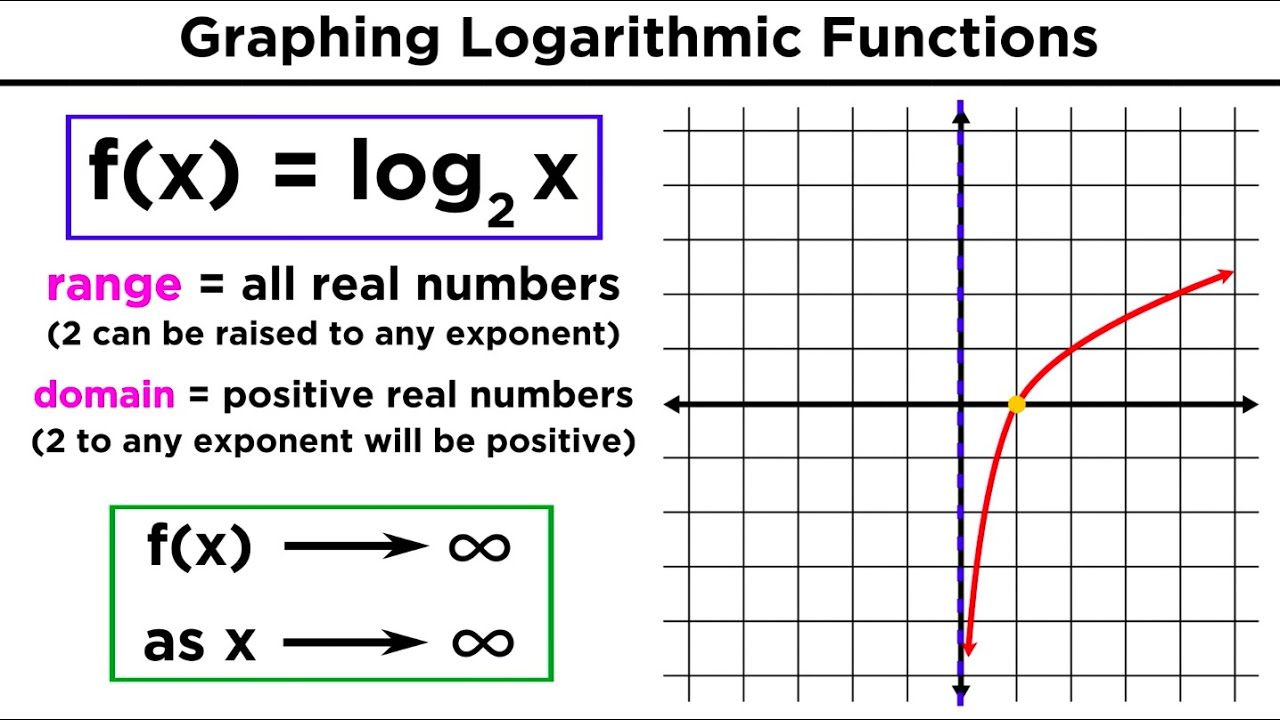
-The domain of a logarithmic function is all positive real numbers, because you cannot have a logarithm of a non-positive number (as the log of 0 and negative numbers are undefined). In interval notation, the domain is (0, ∞).
What is the range of a logarithmic function?
-The range of a logarithmic function is all real numbers, from negative infinity to positive infinity. This is because the output of a log function can be any real number, depending on the input value.
How do you convert a logarithmic equation to exponential form?
-To convert a logarithmic equation to exponential form, you rewrite the equation with the base raised to the power of the variable on the left side and the argument of the log on the right side. For example, if log base 2 of X = Y, you convert it to 2^Y = X.
What is the difference between the horizontal asymptote of an exponential function and a logarithmic function?
-An exponential function has a horizontal asymptote, which is a horizontal line that the graph approaches as the variable moves away from the asymptote. In contrast, a logarithmic function has a vertical asymptote, which is a vertical line at which the graph approaches but never touches or crosses.
How do you solve a logarithmic equation like log base X of 27 = 3 for X?
-To solve the equation log base X of 27 = 3 for X, you convert it to exponential form: X^3 = 27. Since 3^3 is 27, X must be 3 because that is the number whose cube is 27.
What is the inverse function of f(X) = ln(X) + 3 - 1?
-To find the inverse function, you first replace f(X) with Y, switch X and Y, and then solve for Y. The inverse function of f(X) = ln(X) + 3 - 1 is f^(-1)(X) = e^(X + 1) - 3.
How do you determine the extraneous solutions in logarithmic equations?
-An extraneous solution in logarithmic equations is a value that makes the logarithm undefined. For example, if you have log base 2 of (X - 5) = -1, and you find X = -1 as a solution, this is extraneous because you cannot have a log of a negative number (logarithms are only defined for positive real numbers).
What is the process for graphing a logarithmic function?
-To graph a logarithmic function, you first find the vertical asymptote by setting the inside of the log function equal to zero. Then, you find a few points by setting the inside to other values like 1. You plot these points and draw the graph starting from the vertical asymptote, following the points to create the curve.
Outlines
📚 Introduction to Logarithms
This paragraph introduces the concept of logarithms, explaining how to evaluate logs, use the change of base formula, expand and condense logs, solve equations involving logs, and graph logarithmic functions. It begins with the basics of evaluating logs by determining the power to which a base must be raised to obtain a given number, illustrated with examples using different bases like 2, 3, 4, and 5.
📈 Understanding Logarithmic Properties and Functions
The paragraph delves into the properties of logarithms, such as the effects of having a fraction within a log and the implications of the base being larger or smaller than the number inside the log. It also covers how to use the change of base formula to convert logs into natural logs and the properties of logs, like log(a*b) = log(a) + log(b) and log(a/b) = log(a) - log(b). The explanation includes examples and the process of simplifying and expanding logarithmic expressions.
🔢 Solving Logarithmic Equations
This section focuses on solving logarithmic equations by converting them into exponential form and using the properties of logarithms to isolate variables. Examples are provided to demonstrate how to solve for unknowns in various logarithmic expressions, including handling cases where extraneous solutions may arise and need to be discarded based on the domain of the logarithmic function.
📊 Graphing Exponential and Logarithmic Functions
The paragraph discusses the process of graphing exponential and logarithmic functions, highlighting the differences in their asymptotes and growth rates. It explains how to find the horizontal asymptote for exponential functions and the vertical asymptote for logarithmic functions, and how to plot key points to sketch the graphs. The paragraph also describes the transformations of these graphs based on the signs of the exponent and the coefficient in front of the base for exponential functions, and the base for logarithmic functions.
🌐 Domain and Range of Logarithmic Functions
This part of the script focuses on determining the domain and range of logarithmic functions. It emphasizes that the domain of a logarithmic function is restricted to positive real numbers, starting from a certain value to infinity, based on the vertical asymptote. The range of logarithmic functions is all real numbers, from negative infinity to infinity. The paragraph also revisits the domain and range of exponential functions, contrasting them with logarithmic functions.
🔄 Inverse Functions: Logarithmic and Exponential
The final paragraph of the script discusses the concept of inverse functions, specifically between logarithmic and exponential functions. It explains how to find the inverse function by interchanging the roles of x and y and solving for y. The paragraph also illustrates the symmetry of inverse functions across the line y=x, providing an example of graphing both a logarithmic function and its exponential inverse, and how to find the asymptotes and key points for the inverse function.
Mindmap
Keywords
💡Logarithms
💡Change of Base Formula
💡Exponential Functions
💡Graphing
💡Asymptotes
💡Domain and Range
💡Inverse Functions
💡Natural Logarithm
💡Solving Equations
💡Properties of Logs
Highlights
The video begins with an introduction to logarithms, explaining how to evaluate logs and their applications in various mathematical operations.
The concept of logarithms is illustrated through examples, such as log base 2 of 4, which is asking what power of 2 equals 4, and the answer is 2 because 2 squared equals 4.
The change of base formula is introduced, which allows for the conversion of logarithms from one base to another, using the formula log base a of B equals log base B over log a.
Logarithmic properties are discussed, including log a plus log B equals log a times B, and log a minus log B equals log a divided by log B.
The video demonstrates how to expand and condense logarithmic expressions using logarithmic properties, such as combining logs with the same base into a single log.
Examples of solving logarithmic equations are provided, showing how to isolate variables and find their values using logarithmic manipulations.
The video explains how to graph logarithmic functions, including determining vertical asymptotes and plotting key points based on the function's properties.
Inverse functions are introduced, with a focus on how to find the inverse of a logarithmic function and its relationship to exponential functions.
The process of graphing exponential functions is detailed, including finding horizontal asymptotes and using them to plot the function's graph.
The video emphasizes the importance of understanding the domain and range of both exponential and logarithmic functions for accurate graphing and problem-solving.
Practical applications of logarithms, such as solving real-world problems involving growth and decay, are hinted at as part of the broader mathematical toolbox.
The video concludes with a summary of the key points covered, reinforcing the understanding of logarithms, their properties, and their graphical representations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: