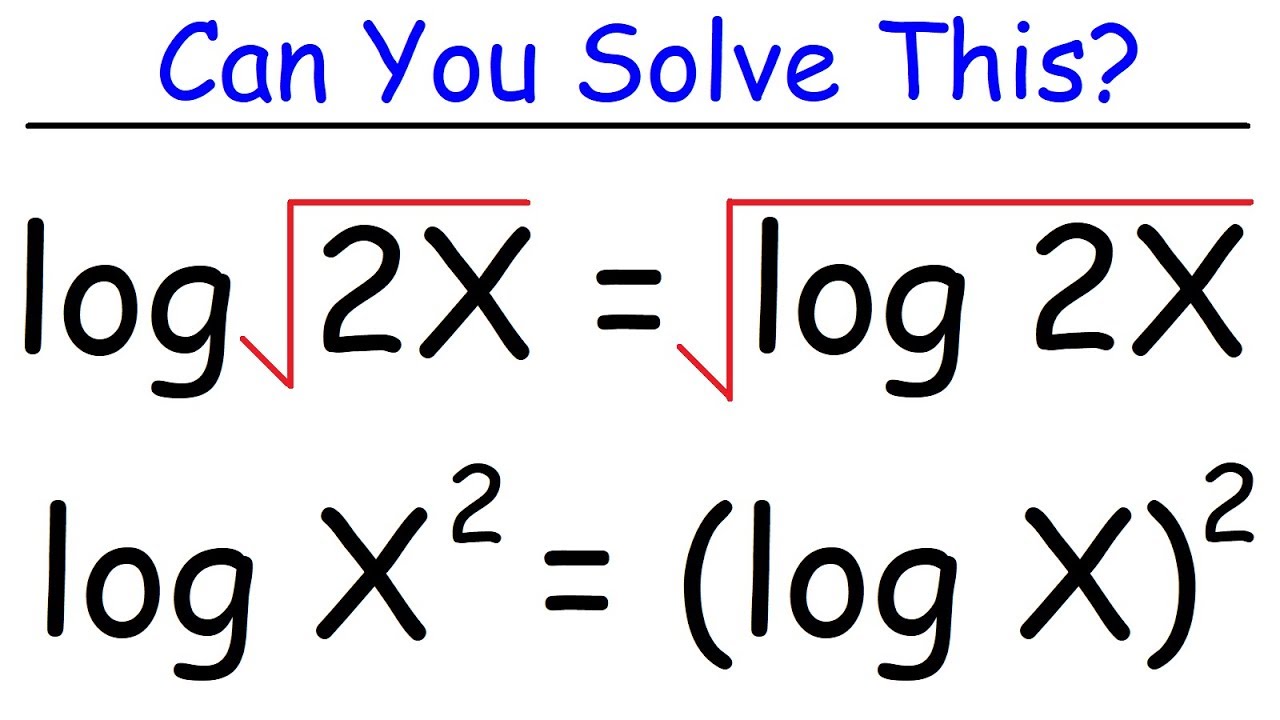Solving Complex Logarithmic Equations
TLDRThis educational video script guides viewers through solving complex logarithmic equations by converting them into exponential form. It demonstrates the process using two examples, starting with simplifying an equation involving multiple logarithms and ending with a nested logarithmic expression. The script emphasizes the importance of understanding logarithmic properties and provides a step-by-step approach to isolate and solve for the variable. It also includes a verification method to ensure the correctness of the solution, showcasing the application of logarithmic rules and the change of base formula.
Takeaways
- 📚 The video script provides a step-by-step guide on solving complex logarithmic equations.
- 🔢 It emphasizes the importance of converting logarithmic expressions into exponential form to simplify the problem-solving process.
- 👉 The formula \( \log_a(b) = c \) can be transformed into its exponential form as \( a^c = b \).
- 📐 The script uses an example where \( \log_4(64) = 3 \) is converted to \( 4^3 = 64 \) to demonstrate the concept.
- 🔑 The first step in solving the given complex logarithmic problem is to express everything in terms of a single base raised to a power.
- ➖ The script shows subtraction as a method to isolate the logarithmic expressions and simplify the equation.
- 🔄 It repeats the process of converting logarithmic expressions into exponential form to further simplify the equation.
- 📉 The script demonstrates subtracting constants from both sides of the equation to isolate the variable.
- 📈 The final step involves converting the remaining logarithmic expression into an exponential form to solve for the variable.
- 🔍 The script suggests verifying the solution by substituting the found value back into the original equation.
- 📝 It also illustrates an alternative problem with nested logarithms and shows how to apply the same principles to solve it.
- 📉 The use of properties of logarithms, such as moving exponents in front of the logarithm, is highlighted as a simplification technique.
- 📚 The script concludes by reiterating the importance of understanding logarithmic properties to solve complex equations effectively.
Q & A
What is the first step in solving a complex logarithmic equation?
-The first step is to convert the logarithmic expression into an exponential form.
How do you convert a logarithmic expression to an exponential form?
-You can convert a logarithmic expression by following the formula: log base a of b is equal to c can be written as a raised to the c is equal to b.
Using the formula, how would you convert log base 4 of 64 equals 3 to its exponential form?
-You would convert it to 4 raised to the third power is equal to 64.
In the provided example, what is the next step after converting 3 squared to 9?
-The next step is to subtract 7 from both sides of the equation.
After simplifying the equation to 2 equals log base 4 of 13 plus log base 2 of x plus 4, what is the next step?
-The next step is to convert the logarithmic expression to an exponential form again, resulting in 4 squared equals 13 plus log base 2 of x plus 4.
How do you solve 4 squared equals 13 plus log base 2 of x plus 4?
-You subtract 13 from both sides to get 3 equals log base 2 of x plus 4, then convert it to its exponential form: 2 raised to the third power equals x plus 4.
What value of x solves the equation 2 to the third power equals x plus 4?
-The value of x is 4.
How do you verify the solution to the logarithmic problem?
-You rewrite the problem and replace x with the solution to check if the equation holds true.
What does log base 2 of 8 equal to, and why?
-Log base 2 of 8 equals 3 because 2 raised to the third power is 8.
In the second example, what is the first step after converting the logarithmic expression into its exponential form?
-The first step is to calculate 2 raised to the third power, which is 8, and set it equal to log base 4 of x raised to the 16th.
How do you simplify 8 equals 16 times log base 4 of x?
-You divide both sides by 16 to get 1/2 equals log base 4 of x.
What is the final step to solve 4 raised to the one-half equals x?
-You take the square root of 4 to find x, which equals 2.
How do you verify the solution to the second example problem?
-You substitute x with the solution in the original equation and use logarithmic properties and change of base formula to check if the equation holds true.
What does log base 4 of 2 equal to and why?
-Log base 4 of 2 equals 1/2 because 4 raised to the one-half power is 2.
How can the change of base formula be used to verify the solution in the second example?
-You can convert log base 4 of 2 to log 2 divided by log 4, then simplify to show it equals 1/2.
Outlines
📚 Solving Complex Logarithmic Equations
This paragraph introduces a complex logarithmic equation and encourages viewers to attempt solving it. It reviews the process of converting a logarithmic expression into its exponential form using the formula \( \log_a(b) = c \) which translates to \( a^c = b \). An example is provided where \( \log_4(64) = 3 \) is converted to \( 4^3 = 64 \). The paragraph then walks through the steps of solving the given problem by isolating and converting each logarithmic term into an exponential form, simplifying the equation step by step until the value of \( x \) is found to be 4. The solution process is verified by substituting \( x \) back into the original equation and confirming the correctness of the result.
🔍 Verifying Solutions to Logarithmic Equations
This paragraph focuses on verifying the solution to a logarithmic equation by substituting the found value of \( x \) back into the original problem. It demonstrates the process of checking the correctness of the solution by showing that the logarithmic expressions evaluate to the expected values, confirming that \( x = 4 \) is indeed the correct answer. The paragraph then presents a new problem involving nested logarithms and guides the viewer through the thought process of converting the nested logarithmic expression into an exponential form. It simplifies the equation step by step, using properties of logarithms and the change of base formula, to find that \( x = 2 \). The solution is verified by substituting \( x \) back into the original equation and confirming the correctness of the result using both direct substitution and the change of base formula.
📉 Applying the Change of Base Formula
In this paragraph, the change of base formula is applied to verify the solution to a logarithmic equation. It explains how to use the formula \( \log_a(b) = \frac{\log_c(b)}{\log_c(a)} \) to evaluate \( \log_4(2) \) and shows that it simplifies to \( \frac{1}{2} \). The paragraph then demonstrates the verification process by substituting \( x = 2 \) back into the original equation, showing that the logarithmic expression simplifies correctly to 3, confirming the solution. The change of base formula is used again to express \( \log_8(2) \) in terms of \( \log_2 \) and to confirm the correctness of the solution through a different method, reinforcing the accuracy of the result.
Mindmap
Keywords
💡Logarithmic Equation
💡Exponential Form
💡Logarithmic Properties
💡Change of Base Formula
💡
💡Logarithmic Expression
💡Base of a Logarithm
💡Power Rule of Logarithms
💡Solving Logarithmic Equations
💡Verification of Solution
💡Logarithmic Functions
💡Square Root
Highlights
Introduction to solving complex logarithmic equations by converting logarithmic expressions into exponential forms.
Explanation of the conversion process: log base a of b equals c can be transformed into a raised to the c equals b.
Example provided: log base 4 of 64 equals 3 is converted to 4 raised to the third power equals 64.
Application of the conversion process to the problem: 3 squared equals 7 plus log base 4 of 13 plus log base 2 of x plus 4.
Simplification of the equation: 3 squared is 9, resulting in 9 equals 7 plus the logarithmic terms.
Subtraction of 7 from both sides: 2 equals log base 4 of 13 plus log base 2 of x plus 4.
Further conversion: 4 squared equals 13 plus log base 2 of x plus 4.
Simplification of the second equation: 4 squared is 16, leading to 16 minus 13 equals 3 equals log base 2 of x plus 4.
Final conversion: 2 to the third power equals x plus 4.
Solution: 2 to the third power is 8, so 8 equals x plus 4, resulting in x equals 4.
Verification of the solution by substituting x equals 4 back into the original equation.
Explanation of the verification process, showing each step and confirming the correctness of the solution.
Introduction to a second example problem: log base 2 of log base 4 of x raised to the 16th power equals 3.
Step-by-step solution of the second problem, starting with converting log base 2 of log base 4 of x raised to the 16th power equals 3 into exponential form.
Final solution of the second problem: x equals 2, followed by a thorough verification process to confirm the correctness.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: