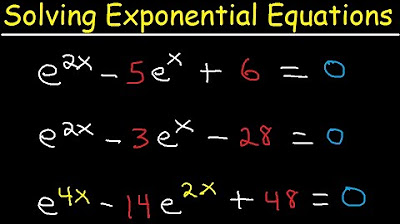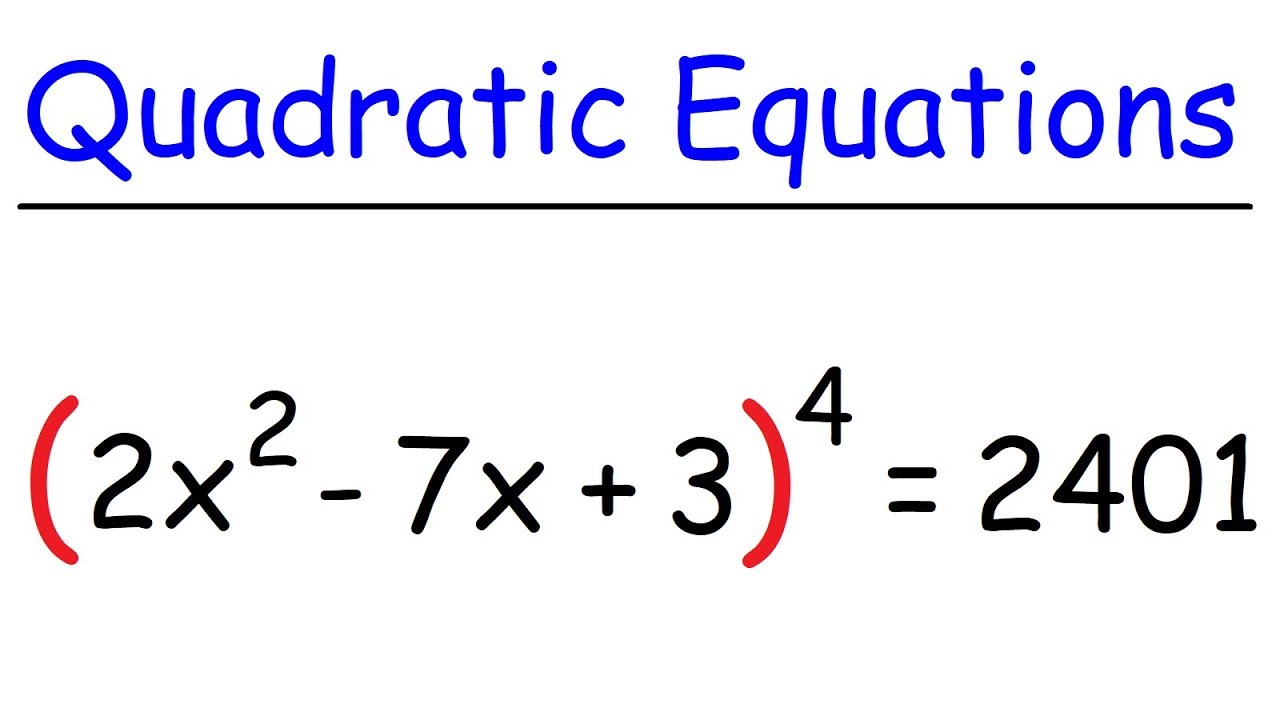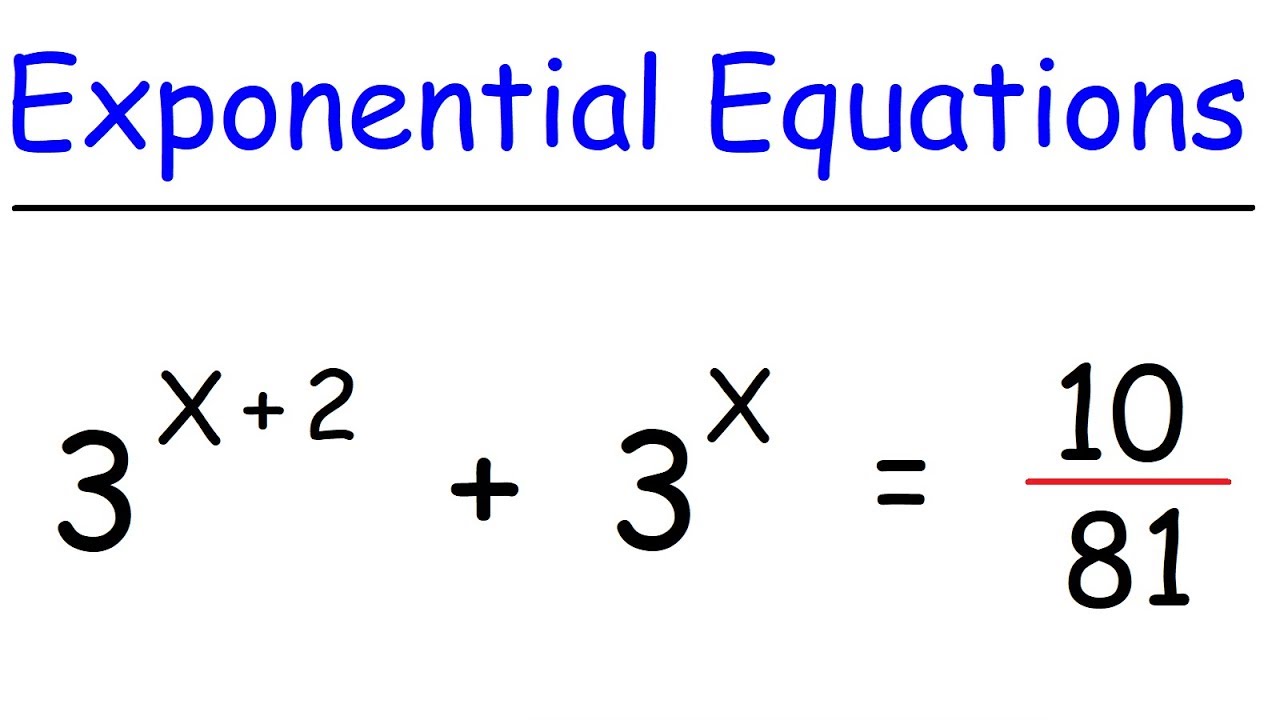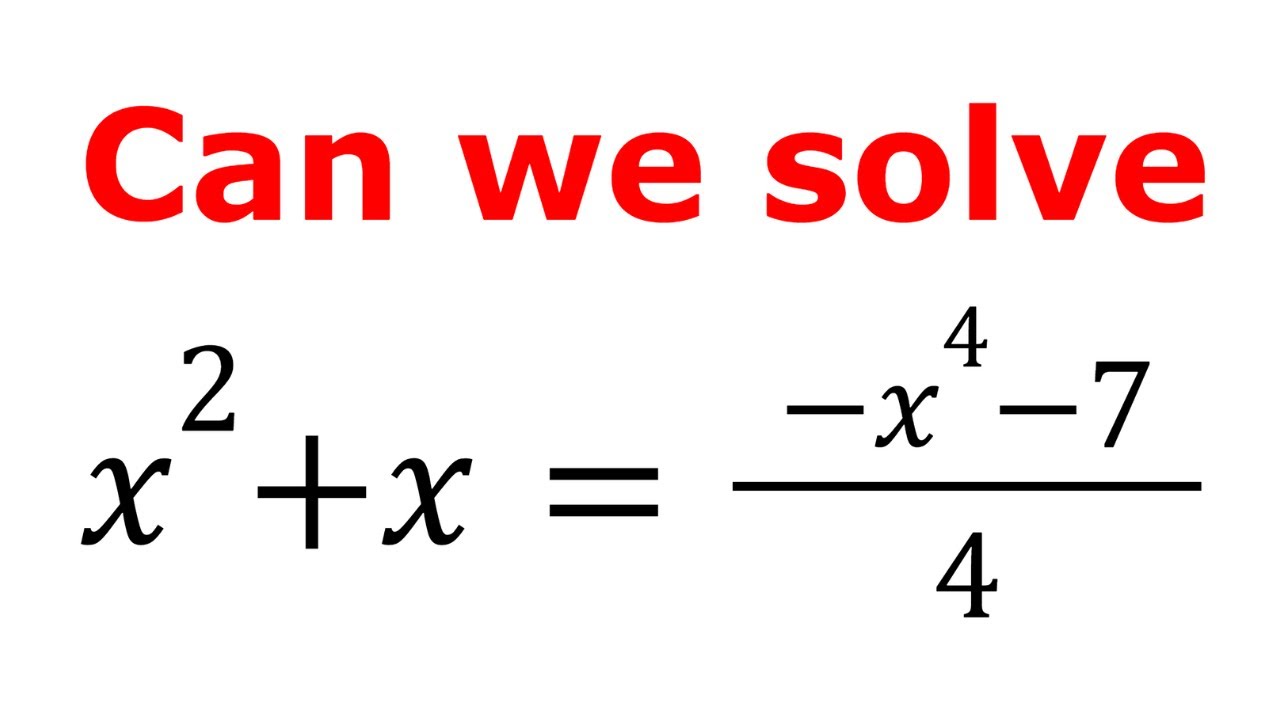Can you solve this? | Exponential Equation | Algebra Problem.
TLDRIn this mathematical tutorial, the video explains the process of solving a quadratic equation by focusing on balancing the bases and applying the laws of indices. The problem involves simplifying an expression with a base of 2 and power of 3, equating it to a variable x, and then solving for x. The method involves multiplying powers with the same base, applying the square root to both sides, and ultimately factoring to find the two possible solutions for x, which are x = 0 and x = 1/9. The video concludes with an invitation to share the content and a farewell from the presenter, Jacob.
Takeaways
- 📚 The script discusses a mathematical problem involving exponents and roots.
- 🔢 It begins with the equation 2^(3*X) = a^(2^3), emphasizing the importance of balancing bases.
- 🤔 The video explains that when dealing with powers, you multiply the exponents to simplify the equation.
- 🧮 After simplifying, the equation becomes 2^(3*X) = 2^3, which is equivalent to 8, by the laws of indices.
- 👌 The video then equates the exponents, since the bases are the same, leading to the equation 3*X = 3.
- 🔍 The problem is solved for X by applying the square root to both sides of the equation.
- 📈 The result is a quadratic equation, x^2 - 9x = 0, which will yield two solutions.
- 🌟 The solutions are found by factoring the equation: x = 0 and 1 - 9x = 0, leading to x = 1/9.
- 🎓 The video is educational, focusing on solving a specific type of mathematical problem.
- 🙏 The speaker, Jacob, encourages viewers to share the video as a way to support the content.
Q & A
What is the main concept discussed in the video?
-The main concept discussed in the video is solving a quadratic equation by balancing the bases and applying the laws of indices.
How does the video begin the process of solving the equation?
-The video begins by identifying the need to balance the bases, starting with the equation 2^3 * X and simplifying it to 2^(3+1) or 2^4.
What law of indices is mentioned in the video?
-The law of indices mentioned is that when you have the same base, a^m is equal to a^n, allowing you to equate the powers as long as the bases are the same.
How does the video proceed to simplify the equation after equating the powers?
-After equating the powers, the video applies the square root to both sides of the equation to simplify it further, resulting in X = a^(9/2).
What type of equation does the simplified expression result in?
-The simplified expression results in a quadratic equation.
How does the video find the two solutions to the quadratic equation?
-The video finds the two solutions by factorizing the quadratic equation and setting the expression equal to zero, then solving for X in two separate cases.
What are the two solutions provided in the video?
-The two solutions provided are X = 0 and X = 1/9.
How does the video demonstrate the process of factorization?
-The video demonstrates factorization by rewriting the quadratic equation in the form of (1 - 9X) = 0 and then solving for X in both cases.
What is the significance of the base 2 in this video?
-The base 2 is significant because it is used to balance the bases and simplify the equation according to the laws of indices.
Why is the square root applied in the solution process?
-The square root is applied to eliminate the power from both sides of the equation, simplifying it to a form that can be factorized and solved for X.
What is the final step in solving for X?
-The final step in solving for X is dividing by -9 to isolate X and find the two solutions, 0 and 1/9.
Outlines
📚 Balancing Exponents and Solving Quadratic Equations
The paragraph introduces the concept of balancing bases in exponents, using the example of 2^3 * X = 8 * X. It explains the laws of indices and how to equate powers with the same base. The process of solving for X is detailed, involving the application of the square root to both sides of the equation, transforming it into a quadratic equation. The solution involves factorization and results in two solutions: x = 0 and x = 1/9. The video concludes with a call to action for viewers to share the content.
Mindmap
Keywords
💡Balancing Bases
💡Laws of Indices
💡Powers
💡Equating Powers
💡Square Root
💡Quadratic Equation
💡Factoring
💡Solving for X
💡Exponents
💡Simplifying Equations
💡Jacob
💡Video
Highlights
Balancing the bases in a mathematical equation is crucial for solving it.
The given equation involves a power of base 2, specifically 2^3 * X.
When dealing with powers, the law of indices states that you can multiply powers with the same base.
The equation simplifies to 2^3 * X = 2^3 * a, where 'a' is a constant.
By equating the powers with the same base, we can determine that m = n.
The next step is to apply the square root to both sides of the equation to isolate X.
The equation transforms into a quadratic equation, which will yield two solutions.
The quadratic equation is reformulated as x - 9x^2 = 0.
Factoring x out of the equation gives us x(1 - 9x) = 0.
One solution to the equation is x = 0.
The other solution is derived from setting 1 - 9x equal to zero and solving for x.
By rearranging and dividing by -9, we find the second solution: x = 1/9.
The video is educational, providing a clear walkthrough of solving a quadratic equation.
The presenter, Jacob, invites viewers to share the video for further dissemination of the educational content.
The method demonstrated is applicable to a wide range of similar mathematical problems.
The video's approach to explaining the steps ensures that viewers can follow along easily.
The use of visual aids and clear verbal explanation enhances the learning experience.
The video concludes with a summary of the two solutions to the equation.
The video is a valuable resource for those learning to solve quadratic equations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: