Types of Data: Nominal, Ordinal, Interval/Ratio - Statistics Help
TLDRThis script explores the fundamental types of data: Nominal, Ordinal, and Interval/Ratio, which are crucial for statistical analysis. It explains how data is collected through observations and variables, and how the level of measurement dictates the type of analysis and representation. Nominal data, like sex or chocolate preference, are categorical with no order, summarized by frequency. Ordinal data, such as satisfaction levels, have order but variable intervals, and calculating an average can be controversial. Interval/Ratio data, including age or number of customers, are the most precise, allowing for various mathematical measures. The script also covers appropriate graph representations for each data type and illustrates with an example of a questionnaire used by Helen to gather data for her choconutties business.
Takeaways
- 📊 Data is essential for statistical analysis and understanding phenomena or processes.
- 🔍 Observations are the individual units of interest, such as people, businesses, or time periods.
- 📝 Variables are used to record the measurements of interest, like age, sex, and preferences.
- 🗂 In a spreadsheet, each row represents an observation and each column a variable.
- 📈 The level of measurement for a variable dictates the types of statistics, graphs, and analyses that can be used.
- 🏷 Nominal data is the most basic level, representing categories without order, like sex or chocolate preference.
- 📊 Ordinal data has a meaningful order but with potentially unequal intervals, such as rankings or satisfaction levels.
- 📉 Interval/Ratio data is the most precise, including measurable quantities like age, weight, and customer counts.
- 📊 Nominal data can be summarized with frequencies and visualized using pie charts or bar charts.
- 📊 Ordinal data should be displayed in a logical order, typically using column charts.
- 📈 Interval/Ratio data is versatile and can be summarized with mean, median, and standard deviation, and visualized with bar charts or histograms.
- 📊 The choice of data representation in graphs or charts should match the level of measurement of the data.
Q & A
What is the primary purpose of collecting data in statistical analysis?
-The primary purpose of collecting data in statistical analysis is to find out more about a phenomenon or process. It involves collecting several measures on each person or thing of interest to understand and analyze the subject matter better.
What is an observation in the context of data collection?
-An observation is each thing we collect data about. It could be a person, a business, a product, or a period in time such as a week, depending on the interest of the study.
What is a variable in data collection?
-A variable is a characteristic or factor that records the measurements we are interested in, such as age, sex, and chocolate preference, which can all be stored as variables.
How is data typically organized in a spreadsheet or database?
-In a spreadsheet or database, each row corresponds to a single observation, and each column represents a variable, allowing for an organized and structured way to store and analyze data.
What determines the type of summary statistics, graphs, and analysis that can be used for a variable?
-The level of measurement used for a variable determines which summary statistics, graphs, and analysis are possible and sensible. Different levels of measurement have different analytical implications.
What is the Nominal level of measurement and what are some examples of nominal variables?
-The Nominal level is the most basic level of measurement, also known as categorical or qualitative. Examples of nominal variables include sex, preferred type of chocolate, and color, which are descriptions or labels with no sense of order.
Why can't you calculate a mean or average value for nominal data?
-You cannot calculate a mean or average value for nominal data because nominal values are categorical and do not imply any order or magnitude. They are used to categorize rather than to quantify.
What is the difference between ordinal and nominal data?
-Ordinal data has a meaningful order, unlike nominal data which lacks order. Examples of ordinal data include rank, satisfaction, and fanciness, where there is a clear sequence or hierarchy, although the intervals between values may not be equal.
How should ordinal data be represented in a graph or chart?
-Ordinal data should be represented in a graph or chart that reflects its order, such as a column or bar chart. It is not appropriate to represent ordinal data as a pie chart.
What is the most precise level of measurement and what types of data does it include?
-The most precise level of measurement is interval/ratio, which includes things that can be measured rather than classified or ordered, such as the number of customers, weight, age, and size.
What are some common summary measures for interval/ratio data?
-The most common summary measures for interval/ratio data are the mean, the median, and the standard deviation, which provide a comprehensive understanding of the data's distribution and central tendency.
How should interval/ratio data be represented in a graph or chart?
-Interval/ratio data is best represented as a bar chart or a histogram, which allows for the visualization of grouped data and the distribution of values.
What is the significance of using the appropriate level of measurement when analyzing data?
-Using the appropriate level of measurement is significant because it determines the type of analysis that is sensible for a given dataset. Misapplying levels of measurement can lead to incorrect conclusions and misinterpretations of the data.
Can you provide an example of how Helen used different levels of data in her questionnaire?
-Helen's questionnaire included nominal data like the type of chocolate preferred, which can be shown in a pie or bar chart. Ordinal data such as satisfaction levels and likelihood to buy were represented in a column chart. Interval/ratio data like age, grocery spending, and number of chocolate bars bought were analyzed using mean values and displayed in bar charts or histograms.
Outlines
📊 Understanding Data Types and Their Analysis
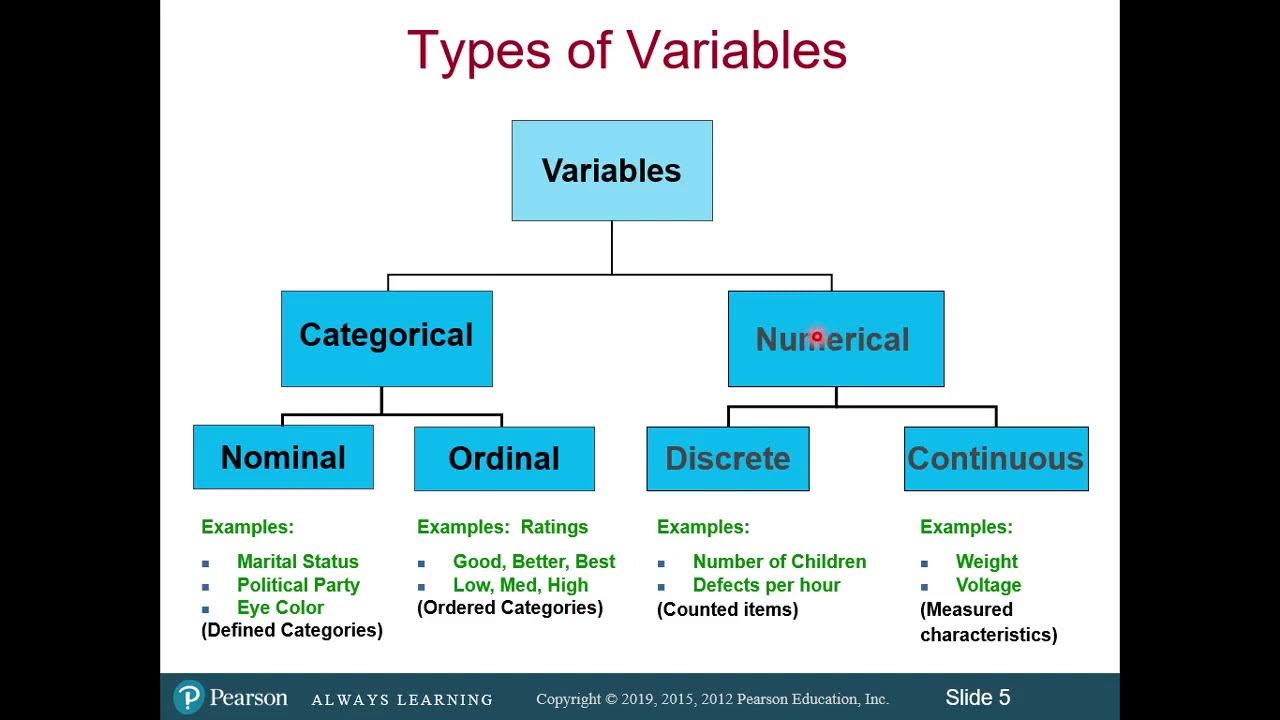
The first paragraph introduces the fundamental concepts of data and its role in statistical analysis. It explains that data is collected to understand phenomena or processes and that each individual or item of interest is an observation. Variables are used to record measurements, and data is organized in spreadsheets or databases with rows representing observations and columns representing variables. The paragraph delves into the different levels of measurement: nominal (categorical or qualitative), ordinal (ordered but with unequal intervals), and interval/ratio (quantitative with equal intervals). It also discusses the types of summary statistics and graphs appropriate for each level, such as frequency or percentage for nominal data, and mean, median, and standard deviation for interval/ratio data. An example is given of Helen, who collects data on customer preferences for her choconutties business, and how she can represent this data visually.
📈 Analyzing Customer Data for Product Development
The second paragraph continues the discussion on data analysis by focusing on Helen's customer data. It provides specific percentages for the types of chocolate preferred by her customers, highlighting the use of pie charts or bar charts for nominal data. For ordinal data, such as satisfaction and likelihood to buy, it suggests using a column chart and discusses the debate around calculating a mean satisfaction score. The paragraph also covers interval/ratio data, presenting the mean age, grocery spending, and chocolate bar purchases of the customers, and how these can be represented in bar charts or histograms. It concludes by emphasizing the importance of choosing the right analysis method based on the level of measurement, with a reference to a video titled 'Choosing the Test' for further information.
Mindmap
Keywords
💡Data
💡Observation
💡Variable
💡Level of Measurement
💡Nominal Data
💡Ordinal Data
💡Interval/Ratio Data
💡Summary Statistics
💡Data Visualization
💡Box Plot
💡Line Chart
Highlights
Data is central to statistical analysis and understanding phenomena or processes.
Observations can be a person, business, product, or a period in time.
Variables record measurements such as age, sex, and chocolate preference.
Data in spreadsheets: each row is an observation, each column a variable.
Level of measurement determines the type of statistics, graphs, and analysis.
Nominal level is the most basic, used for categorical or qualitative data.
Examples of nominal variables include sex, chocolate preference, and color.
Nominal data is summarized using frequency or percentage, not mean.
Ordinal level includes variables with a meaningful order, like rank or satisfaction.
Ordinal data can be summarized by frequency, and mean calculation is debatable.
Interval/Ratio is the most precise level, for measurable quantities like age or weight.
Interval/Ratio data can be discrete or continuous and is mathematically versatile.
Common measures for Interval/Ratio data are mean, median, and standard deviation.
Data representation depends on the level of measurement, e.g., pie charts for nominal.
Ordinal data is best shown in column or bar charts, not pie charts.
Interval/Ratio data is represented as bar charts or histograms for grouped data.
Box plots and line charts are effective for displaying summary statistics and time-series data.
Helen's choconutties example demonstrates the application of different data types.
Type of chocolate preferred is nominal and can be shown in pie or bar charts.
Satisfaction and likelihood are ordinal, shown in column charts with logical order.
Mean satisfaction score calculation for ordinal data is common but requires caution.
Age, groceries spent, and chocolate bars are interval/ratio, displayed in bar charts or histograms.
Mean age, groceries spent, and chocolate bars bought are meaningful summary statistics.
Analysis type depends on the level of measurement, as shown in the 'Choosing the test' video.
Transcripts
Browse More Related Video

Nominal, Ordinal, Interval & Ratio Data: Simple Explanation With Examples

Data Types - Levels of Data Measurements - Nominal Ordinal Interval Ratio | Statistics | Research
Classification of Variables and Types of Measurement Scales

Scales of Measurement in Statistics - Nominal, Ordinal, Interval, Ratio | Level of Measurement

Variables and Types of Variables | Statistics Tutorial | MarinStatsLectures

Introduction to Levels of Measurement: Nominal, Ordinal, Interval, Ratio
5.0 / 5 (0 votes)
Thanks for rating: