Lecture 08: Circles, Pyramids, Cones and Spheres
TLDRThis educational video delves into the fundamental concepts of calculus, focusing on the derivation of formulas for areas and volumes of various shapes. It begins by explaining the area of a circle through a creative method involving breaking the circle into wedges and rearranging them into a rectangle. The video then explores the area of triangles and extends the concept to three-dimensional shapes, such as tetrahedrons, pyramids, and cones, demonstrating how to find their volumes. The surface area of a sphere is also discussed, with an intriguing approach comparing it to a cylinder. Throughout, the video introduces the integral concept by breaking objects into small pieces and summing them up, a method that predates the formal definition of the integral but is mathematically sound.
Takeaways
- 📚 The lecture introduces the concept of integrals through the historical method of deriving formulas for areas and volumes of various shapes.
- 🔍 The formula for the area of a circle (πr^2) is derived by breaking the circle into wedges and rearranging them to form an approximation of a rectangle.
- 📏 Pi (π) is defined as the ratio of a circle's circumference to its diameter, and it is approximately 3.14159.
- 🧩 The area of a triangle is explained as base times height divided by 2, and this principle is extended to more complex shapes by dividing them into smaller, manageable pieces.
- 🏺 The volume of a tetrahedron is deduced to be one-third the area of the base times the height, by comparing it to a prism composed of three identical tetrahedra.
- 🏰 The volume of a pyramid and a cone is explained as being related to the volume of a tetrahedron, with the formula for a pyramid's volume being the base area times height divided by 3.
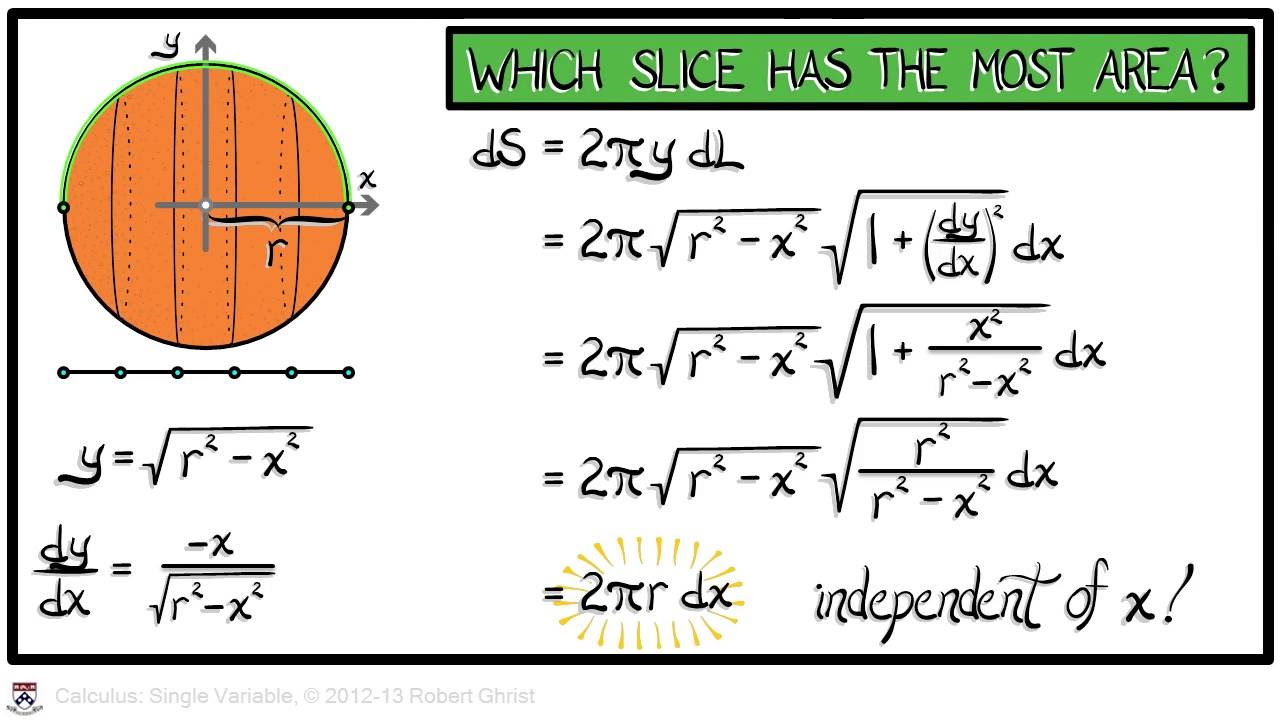
- 🌐 The surface area of a sphere is approached by imagining the sphere being cut by parallel planes and comparing the surface area between these cuts to a cylinder's surface area.
- 🌎 The surprising fact that the surface area between any two parallel cuts of a sphere, regardless of their position, is the same is explained using the geometry of similar triangles.
- ⛓ The concept of integrals is likened to breaking objects into infinitesimally small pieces and summing their contributions to find total areas and volumes.
- 🌕 The final example of the surface area of a sphere being equal to the surface area of an enclosing cylinder (4πr^2) illustrates the power of the integral approach in calculating complex geometric properties.
- 📈 The lecture emphasizes the historical development of integral calculus, highlighting how ancient mathematicians used similar reasoning to modern integral calculus without the formal limit process.
Q & A
What is the main concept discussed in the lecture?
-The main concept discussed in the lecture is the integral, which is the concept of dividing an object into many small pieces and adding them together to deduce the formulas for areas and volumes of various shapes.
Why is the formula for the area of a circle pi times the radius squared?
-The formula for the area of a circle is derived by dividing the circle into many small wedges, rearranging them to form an approximate rectangle, and showing that as the number of pieces increases, the shape becomes indistinguishable from a rectangle with area pi times the radius squared.
What is the relationship between pi and the circumference of a circle?
-Pi is the ratio of the circumference of a circle to its diameter. It is a constant number approximately equal to 3.14159, and the circumference of a circle is pi times the diameter.
How is the area of a triangle related to its base and height?
-The area of a triangle is determined by the length of its base and its height. For any triangle, the area is calculated as one-half times the base times the height.
How can the volume of a tetrahedron be deduced?
-The volume of a tetrahedron can be deduced by considering it as part of a prism, which is made up of three tetrahedra with equal volumes. Since the volume of a prism is the area of its base times its height, each tetrahedron's volume is one-third of that of the prism.
What is the formula for the volume of a pyramid?
-The volume of a pyramid is one-third the area of its base times its height. This is derived by considering the pyramid as composed of two tetrahedra and applying the volume formula for a tetrahedron.
How is the volume of a cone related to its base and height?
-The volume of a cone is one-third the area of its base times its height. This is similar to the formula for a pyramid and is derived by considering the cone as being made up of many small tetrahedra.
What is the surface area of a sphere and how can it be deduced?
-The surface area of a sphere is 4 pi times the radius squared. It can be deduced by imagining the sphere being cut by parallel planes and comparing the surface area between the cuts on the sphere to the area of a band on an enclosing cylinder, showing they are equal.
How does the concept of breaking an object into small pieces relate to the integral?
-The concept of breaking an object into small pieces and adding them together is the underlying philosophy of the integral. It is an ancient idea that was used to derive area and volume formulas before the integral was formally defined in terms of limits.
What is the significance of the lecture's discussion on the ancient concept of the integral?
-The lecture highlights that the ancient concept of breaking objects into small pieces to deduce formulas for areas and volumes is very similar to the modern definition of the integral. It shows that while the ancients did not have a formal definition, their methods were mathematically sound and can be made rigorous with modern understanding.
Outlines
📚 Introduction to Calculus and the Integral Concept
This paragraph introduces the topic of calculus, focusing on the concept of the integral. It explains how the derivative relates to the areas and volumes of objects and sets the stage for the lecture's main theme: finding formulas for areas of objects like circles and volumes of more complex solids such as cones, pyramids, and spheres. The integral is described as the process of dividing an object into many small pieces and summing these to deduce the formula for the whole object. The paragraph also touches on the historical aspect, noting that these ideas predated the formal definition of the integral by thousands of years.
🔍 Deriving the Area of a Circle Using Infinitesimal Pieces
The speaker delves into the derivation of the area of a circle, explaining the well-known formula A = πr². They use a visual approach by dividing a circle into wedges, which are then rearranged to resemble a rectangle. By increasing the number of divisions and rearranging the pieces, the circle's area can be approximated by the area of a rectangle with dimensions r (radius) and πr (half the circumference). This method demonstrates that the area of the circle is equivalent to that of the rectangle, thus confirming the formula for the area of a circle.
📐 Understanding the Area of Triangles and Circles Through Dissection
This section explores the area of triangles, both right and non-right, by dividing them into small horizontal slices. The speaker explains that rearranging these slices does not change the area, leading to the conclusion that the area of any triangle is determined by its base and height, with the formula A = (base * height) / 2. The concept is further extended to the area of a circle, which can be thought of as composed of many tiny triangles, each with an area of (base * height) / 2, summing up to the total area of the circle, πr².
🧊 Volume Deduction for a Tetrahedron and its Relation to a Prism
The speaker discusses the volume of a tetrahedron, a pyramid with a triangular base. They propose a method to deduce its volume by comparing it with a prism, which has a known volume formula (base area * height). The prism is divided into three tetrahedra, and by showing that all three tetrahedra have the same volume, the speaker concludes that the volume of a single tetrahedron is one-third of the prism's volume. This leads to the formula for the volume of a tetrahedron: (base area * height) / 3.
🏺 Extending Volume Formulas to Pyramids, Cones, and Spheres
Building on the previous deduction, the speaker extends the volume formula to pyramids and cones. Pyramids are shown to be composed of two tetrahedra, leading to a volume formula of (base area * height) / 3 for a pyramid. Cones are then considered as an aggregation of many tiny triangles, resulting in a volume formula of (base area * height) / 3 for a cone as well. The speaker also introduces the concept of calculating the surface area of a sphere, setting up the problem for the next paragraph.
🌐 Surface Area of a Sphere: A Geometric Comparison with a Cylinder
The speaker tackles the challenging concept of finding the surface area of a sphere. They propose a thought experiment involving cutting the sphere with planes parallel to the latitude lines and comparing the areas created by these cuts. The surprising revelation is that the surface area between any two such cuts is the same, regardless of the sphere's curvature. The explanation involves comparing the areas on the sphere to those on an enclosing cylinder, demonstrating that the surface area of the sphere is equivalent to the lateral surface area of the cylinder, resulting in a surface area formula of 4πr² for the sphere.
🎯 Conclusion: The Integral's Ancient Origins and Upcoming Exploration of Archimedes' Logic
In conclusion, the speaker reflects on the ancient origins of the integral concept, which was used to break down complex shapes into smaller, manageable pieces to derive area and volume formulas. They highlight the persuasive logic of the ancients, which, while not rigorous by modern standards, led to correct mathematical results. The speaker anticipates the next lecture, where they will explore Archimedes' use of this logic to deduce the volume of a sphere, thus continuing the exploration of calculus and the integral.
Mindmap
Keywords
💡Derivative
💡Integral
💡Area
💡Volume
💡Circle
💡Triangle
💡Tetrahedron
💡Prism
💡Cone
💡Sphere
Highlights
Introduction to the concept of integrals through dividing objects into small pieces and adding them together to derive formulas for areas and volumes.
Explanation of the area of a circle formula derivation by breaking the circle into wedges and rearranging them into a rectangle shape.
The relationship between pi and the circle's circumference to diameter ratio, and how it leads to the area formula of pi times radius squared.
Visual demonstration of increasing the number of pieces from eight to sixteen and the transition to a rectangle shape for the circle area derivation.
Derivative of the area of a circle being equal to its circumference, with the formula derivation of 2 pi r.
Simple method for calculating the area of a right triangle and the transition to finding the area of any triangle by dividing it into horizontal slices.
The concept that the area of a triangle is determined by its base and height, regardless of the position of the top point.
Graphical illustration of sliding horizontal bands to rearrange a triangle into a right triangle for area calculation.
Introduction of the tetrahedron and the method of finding its volume by comparing it to a prism made up of three tetrahedra.
Explanation of how the volume of a prism can be used to deduce the volume of a tetrahedron, resulting in the formula one-third base area times height.
Derivation of the volume formula for a pyramid by considering it as composed of two tetrahedra and applying the derived tetrahedron volume formula.
Volume of a cone derivation by considering it as an infinite sum of tetrahedra and applying the tetrahedron volume formula.
Introduction to the concept of computing the surface area of a sphere and the challenge it presents due to its curved surface.
Strategy to find the surface area of a sphere by imagining cutting the sphere with parallel planes and comparing the areas.
The surprising fact that the surface area between any two parallel cuts on a sphere is the same, regardless of the sphere's position.
Use of a cylinder to compare and prove that the surface area of a sphere can be calculated as 4 pi r squared.
The ancient concept of breaking objects into small pieces to derive area and volume formulas, which is the foundation of modern integral calculus.
Upcoming lecture teaser on Archimedes' method for deducing the volume of a sphere using similar logic to the concepts discussed.
Transcripts
Browse More Related Video

Lecture 09: Archimedes and the Tractrix
Calculus Chapter 4 Lecture 36 Surface Area

Three-Dimensional Shapes Part 1: Types, Calculating Surface Area

Definite Integrals from Graphs (Part 1 of 3)
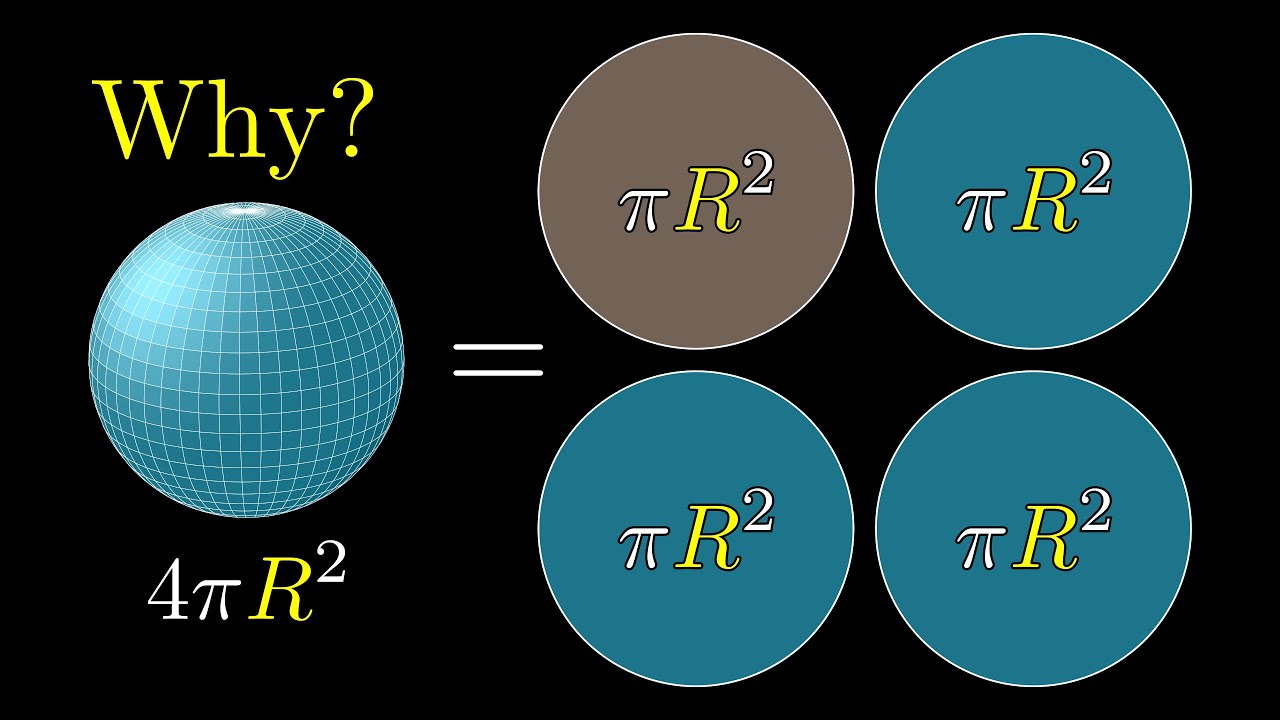
But why is a sphere's surface area four times its shadow?

Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method
5.0 / 5 (0 votes)
Thanks for rating: