What is Calculus - Lesson 4 | Integration | Don't Memorise
TLDRThis educational video script explores the concept of calculating areas of various shapes, from regular polygons to complex curved regions. It introduces the method of exhaustion used by ancient Greeks to approximate areas, such as that of a circle, by inscribing regular polygons. The script also delves into the quadrature of the parabola, a significant achievement by Archimedes, who used triangles to find areas under curves. The video then transitions to the modern approach using calculus and integration, which provides a general method to calculate areas under any curve by approximating with rectangles. The script concludes by highlighting the importance of understanding functions in mathematics, setting the stage for future discussions on differentiation and integration.
Takeaways
- 📐 The area of a regular polygon can be found by dividing it into triangles and summing their areas.
- 📏 Calculus, specifically integration, is used to calculate areas of regions bounded by curved lines, which cannot be done with simple geometric shapes.
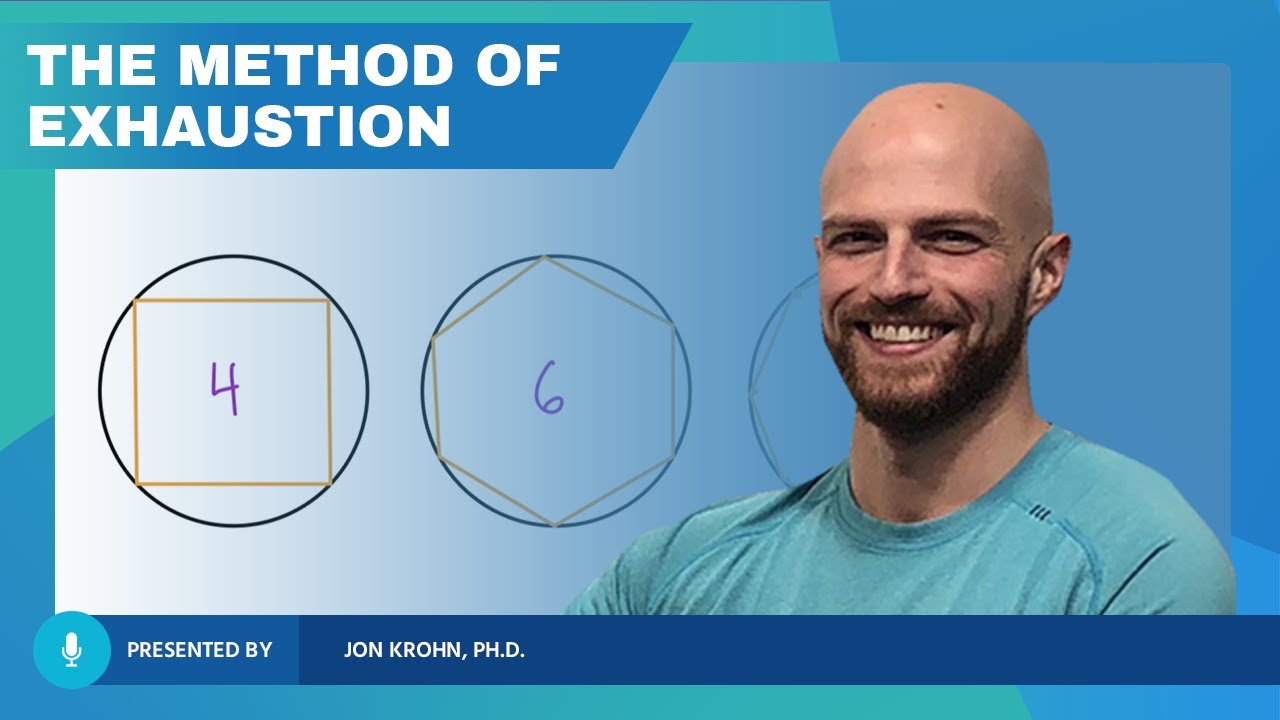
- 🔍 Ancient Greek mathematicians, like Archimedes, used the method of exhaustion to approximate areas of curved shapes, such as circles and parabolas.
- 📉 The method of exhaustion involves placing shapes like regular polygons or triangles around a figure to approximate its area.
- 📐 Archimedes' quadrature of the parabola involved using triangles to find the area under a parabola and a chord.
- 📚 The concept of limits is fundamental in calculus, both for differentiation and integration.
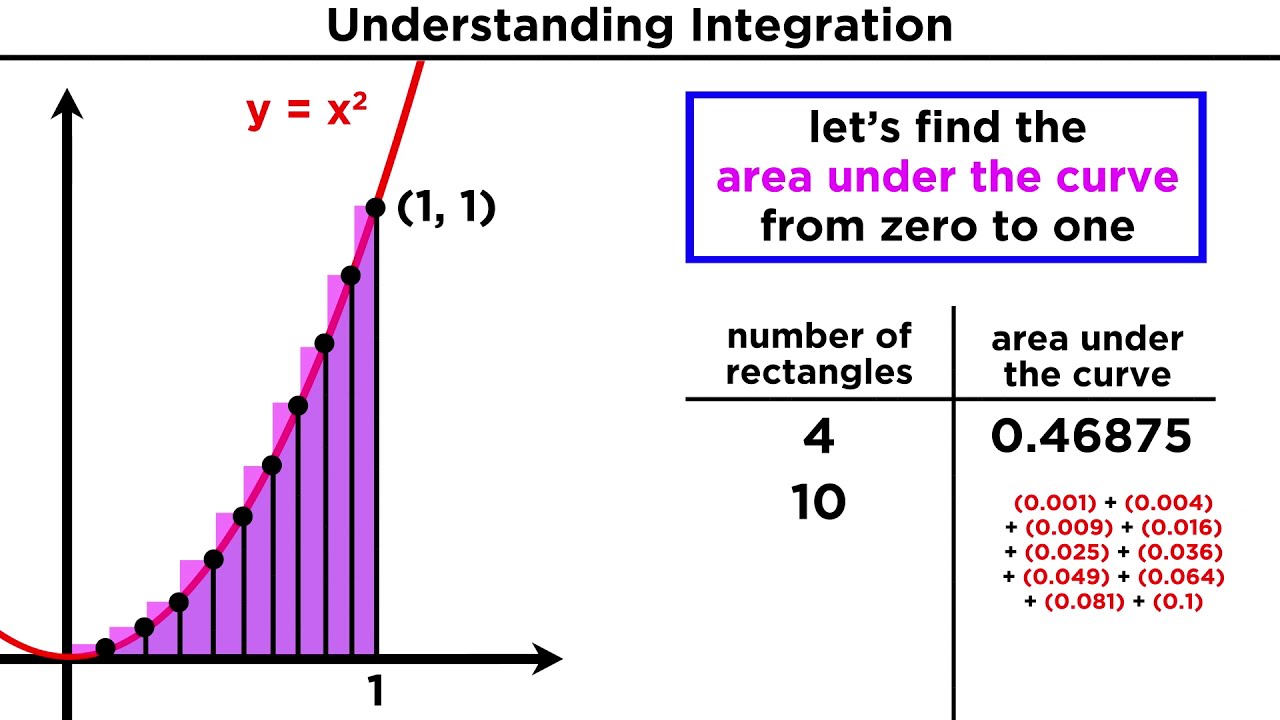
- 📈 Integration is a process that can be used to find areas under curves and volumes of solids by summing infinitesimally small rectangles.
- 📊 The area under a curve can be approximated by dividing the interval under consideration into smaller parts and summing the areas of rectangles formed by the minimum and maximum 'Y' values in each part.
- 📉 The lower sum and upper sum are terms used to describe the approximations of the area under a curve, with the lower sum always being less than and the upper sum always being greater than the actual area.
- 🔧 Differentiation and integration are presented as opposite processes in calculus, with differentiation finding instantaneous rates of change and integration finding areas under curves.
- 🔄 The script suggests that understanding functions is crucial to grasping the full significance of mathematical concepts like differentiation and integration.
Q & A
How can we find the area of a regular polygon?
-The area of a regular polygon can be found by dividing it into triangles and summing up the areas of these triangles. In the script, it is mentioned that the area of the regular polygon will be the sum of the areas of 8 triangles.
What is the method of exhaustion used for?
-The method of exhaustion is an ancient technique used for finding the area of shapes, especially those with curved boundaries like a circle. It involves inscribing and circumscribing polygons around the shape and using the areas of these polygons to approximate the area of the curved shape.
How did Archimedes find the area of a region bounded by a parabola and a chord?
-Archimedes used the method of exhaustion with triangles instead of polygons. He chose a point on the curve where the tangent line is parallel to the chord and used this to create triangles whose areas, when summed up, approached the area under the parabola.
What is the quadrature of the parabola?
-The quadrature of the parabola is a result proved by Archimedes which states that the area bounded by a parabola and a chord can be found by multiplying 'four over three' times the area of a specific triangle formed by the tangent line parallel to the chord.
How does calculus help in finding areas of regions bounded by curved lines?
-Calculus, specifically through the process of integration, provides a general method to calculate the area of any region, regardless of its shape. It is based on the idea of limits and can handle complex shapes that cannot be decomposed into simple triangles and rectangles.
What is the general approach to finding the area under a curve?
-The general approach to finding the area under a curve is through integration. It involves dividing the area into small rectangles, calculating the sum of their areas, and as the division becomes finer, the sum approaches the actual area under the curve.
What are the lower and upper sums in the context of integration?
-The lower sum is the sum of the areas of rectangles formed by taking the minimum 'Y' value in each part of the divided interval, which is always less than the actual area under the curve. The upper sum is the sum of the areas of rectangles formed by taking the maximum 'Y' value, which is always greater than the actual area under the curve.
How does integration relate to finding the volume of a solid?
-Integration can be used to find the volume of a solid by considering the area under a curve and rotating it. For example, if you know the area under a curve above the X-axis, rotating this area by 360 degrees will give you the volume of an elongated sphere.
What is the significance of the points with minimum and maximum 'Y' values on a curve?
-The points with minimum and maximum 'Y' values on a curve are significant because they represent the extreme points of the curve, which are essential in determining the bounds for the area under the curve and in the process of integration.
How does the process of integration relate to differentiation?
-Integration and differentiation are fundamental processes in calculus that are closely related. Differentiation is the process of finding the instantaneous rate of change of a quantity, while integration is the process of finding the area under a curve. They can be seen as opposite processes, with integration often being the reverse of differentiation.
Outlines
📐 Understanding Regular Polygons and Curved Shapes
The script begins by introducing the concept of finding the area of a regular polygon through the decomposition into triangles. It highlights that while this method works for polygons, it's not applicable for regions bounded by curved lines, which leads to the introduction of Calculus and the process of Integration. The script also delves into historical methods such as the method of EXHAUSTION used by ancient Greek mathematicians to estimate areas of circles and parabolas. It explains how Archimedes used triangles to find the area under a parabola, which is a significant achievement in the field of geometry.
📚 The Evolution to a General Method: Integration
This paragraph discusses the limitations of using shapes like triangles and rectangles to find areas bounded by curved lines and introduces the need for a general method. It presents the idea of using rectangles to approximate the area under a curve, which is the essence of Integration. The script explains how by dividing the area into smaller parts and summing the areas of rectangles, we can get closer to the actual area under the curve. It also hints at the applications of this method in finding volumes and lengths of curves, setting the stage for further exploration in upcoming videos.
📉 The Fundamentals of Integration and Its Applications
The final paragraph provides a deeper understanding of the process of Integration, explaining how it involves dividing an interval into smaller parts and using the minimum and maximum 'Y' values to calculate approximate areas, known as lower and upper sums. As the interval is divided into increasingly smaller parts, these sums approach the actual area under the curve. The script connects this process to differentiation, which is used to find instantaneous rates of change, and teases the upcoming topic of functions, which will further clarify the concepts of differentiation and integration. It concludes with a call to action for viewers to subscribe for more educational content.
Mindmap
Keywords
💡Regular Polygon
💡Integration
💡Method of Exhaustion
💡Parabolas
💡Archimedes
💡Quadrature of Parabola
💡Differentiation
💡Limits
💡Rectangles
💡Functions
Highlights
Finding the area of a regular polygon can be decomposed into the sum of areas of triangles.
Calculus and the concept of limits are introduced as a method to calculate areas of regions bounded by curved lines.
Ancient Greek mathematicians used the method of exhaustion to estimate areas of shapes like circles.
Archimedes found the area between a parabola and a chord using triangles and the method of exhaustion.
Archimedes' quadrature of the parabola is explained through the use of triangles and infinite series.
The need for a general method to find areas bounded by different kinds of curved lines is discussed.
Rectangles are introduced as a general method to approximate the area under a curve.
The process of finding areas and volumes can often be reduced to finding the area under a curve.
The importance of understanding the minimum and maximum 'Y' values on a curve for area calculation is highlighted.
The concept of lower and upper sums is introduced for approximating the area under a curve.
Integration is presented as the process of combining parts to form a whole, specifically for finding areas under curves.
Differentiation and integration are hinted as opposite processes in the study of calculus.
The upcoming video will focus on the concept of functions, which is central to understanding calculus.
The method of exhaustion is explained as an ancient technique for approximating areas of curved shapes.
The parabolic path of a thrown object is related to the concept of a parabola in mathematics.
The importance of the tangent line being parallel to the chord in Archimedes' method is discussed.
The concept of infinite terms and their sum approaching a certain value in the context of calculus is introduced.
Transcripts
Browse More Related Video

Simpson's Rule: Deriving the Basic Form (1 of 2)
What is Integration? Finding the Area Under a Curve
The Method of Exhaustion – Topic 44 of Machine Learning Foundations

Lecture 09: Archimedes and the Tractrix

Business Calculus - Math 1329 - Section 5.3 - The Definite Integral and Fundamental Thm of Calculus

Calculus: Why does integrating a function give area under its curve?
5.0 / 5 (0 votes)
Thanks for rating: