Function inverse example 1 | Functions and their graphs | Algebra II | Khan Academy

Khan Academy
17 Jul 201006:44
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides a detailed walkthrough of finding the inverse of a function. It begins with the function f(x) = -x + 4, graphically represented on a coordinate plane. The process involves setting y = f(x) and solving for x in terms of y to find the inverse function, which turns out to be f^(-1)(x) = -x + 4, identical to the original function. The script also discusses the concept of a function being its own inverse, graphically illustrating this by reflecting the function over the line y = x. The video further explains the mapping between inputs and outputs for both the original and inverse functions, ensuring the reflection makes sense. Lastly, it demonstrates the process with another function g(x) = -2x - 1, deriving its inverse g^(-1)(x) = -x/2 - 1/2 and confirming its reflection over y = x.

Takeaways
  • 📚 The script explains the process of finding the inverse of a function.
  • 🔍 It starts with the function f(x) = -x + 4 and its graphical representation.
  • 📐 To find the inverse, the variable y is set equal to f(x), and then x is solved in terms of y.
  • ➡️ The inverse function is derived by algebraic manipulation: y - 4 = -x, leading to x = -y + 4.
  • 🔄 The script demonstrates that the function f(x) = -x + 4 is its own inverse.
  • 📈 The y-intercept of the function and its inverse is 4, indicating they are identical.
  • 🤔 The concept of reflection over the line y = x is discussed to understand the relationship between a function and its inverse.
  • 📊 The script uses examples to show how inputs and outputs are mapped by the function and its inverse.
  • 📉 For the function g(x) = -2x - 1, the inverse is found to be g^(-1)(x) = (-y/2) - 1/2.
  • 📈 The inverse function g^(-1)(x) has a y-intercept of -1/2 and a slope of -1/2.
  • 🤓 The process of finding an inverse function involves algebraic steps to solve for the input variable in terms of the output variable.
Q & A

  • What is the function f(x) described in the transcript?

    -The function f(x) is described as f(x) = -x + 4.

  • How is the inverse of a function found?

    -To find the inverse of a function, you set y equal to the function, then solve for x in terms of y, which gives you the inverse function.

  • What is the inverse function of f(x) in the transcript?

    -The inverse function of f(x) is f^(-1)(x) = -x + 4, which is identical to the original function when y is replaced with x.

  • How does the graph of the inverse function relate to the graph of the original function?

    -The graph of the inverse function is a reflection of the original function over the line y=x.

  • What is the y-intercept of the function f(x) = -x + 4?

    -The y-intercept of the function f(x) = -x + 4 is 4.

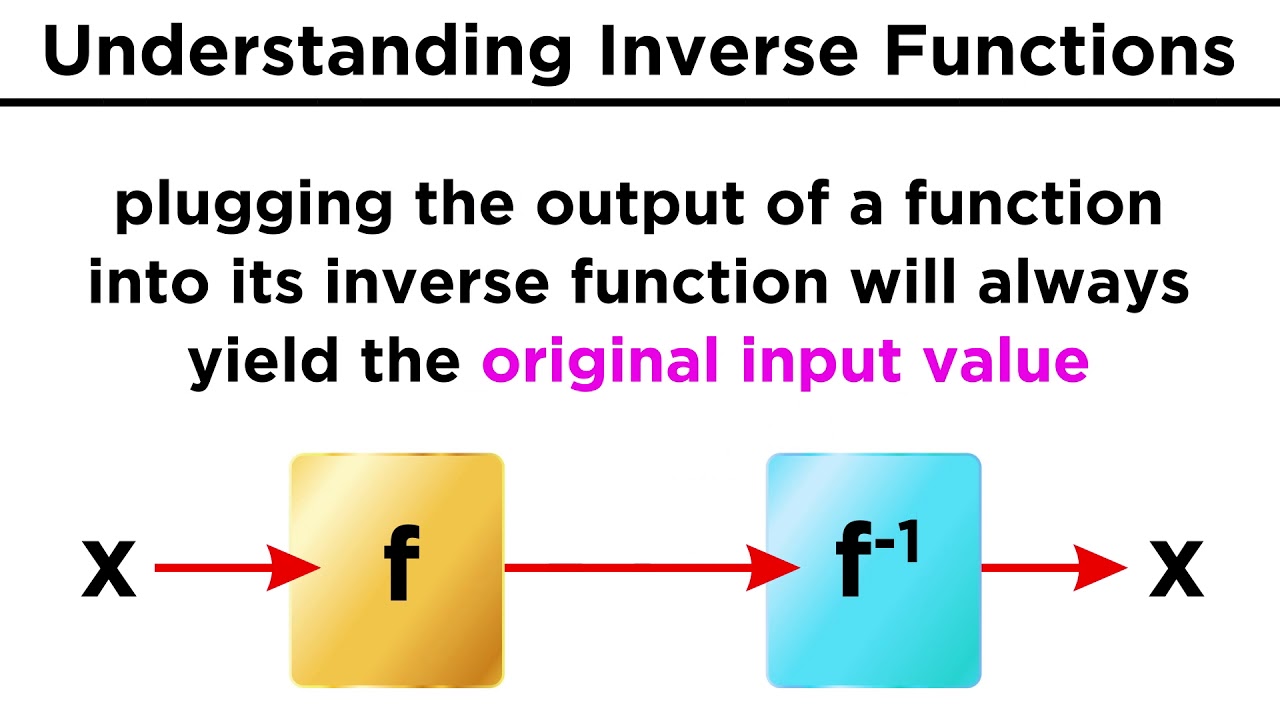
  • What does it mean for a function to be its own inverse?

    -A function is its own inverse if applying the function and then its inverse to any input returns the original input.

  • How does the function g(x) = -2x - 1 relate to its inverse?

    -The inverse of g(x) is found by setting y = g(x), then solving for x in terms of y, resulting in g^(-1)(x) = -(y/2) - 1/2.

  • What is the y-intercept of the inverse function g^(-1)(x) = -(y/2) - 1/2?

    -The y-intercept of the inverse function g^(-1)(x) is -1/2.

  • How does the slope of the inverse function relate to the slope of the original function?

    -The slope of the inverse function is the negative reciprocal of the slope of the original function.

  • What is the domain and range of the function f(x) = -x + 4?

    -The domain and range of the function f(x) = -x + 4 are all real numbers, as it is a linear function.

  • How can you verify if a function and its inverse are correct?

    -You can verify a function and its inverse by checking if the function maps an input to an output, and the inverse maps that output back to the original input.

  • What is the significance of the line y=x in the context of a function and its inverse?

    -The line y=x is significant because it represents the line over which a function and its inverse are reflections of each other.

Outlines
00:00
📚 Finding the Inverse Function

This paragraph explains the process of finding the inverse of a given function. The function f(x) = -x + 4 is introduced, and its graph is discussed. The inverse is found by setting y = f(x) and solving for x in terms of y, resulting in x = -y + 4. The inverse function is then rewritten with x as the input, yielding f^(-1)(x) = -x + 4. The paragraph also explores the concept that the function is its own inverse, as demonstrated by its reflection over the line y = x and by checking the mapping of inputs and outputs for both functions.

05:02
📈 Graphing and Understanding Inverse Functions

The second paragraph delves into graphing the inverse function and understanding its relationship to the original function. The function g(x) = -2x - 1 is presented, and the inverse is derived by solving for x in terms of y, resulting in g^(-1)(x) = -x/2 - 1/2. The y-intercept and slope of the inverse function are identified, and its graph is sketched. The paragraph concludes with a discussion on the reflection of the inverse function over the line y = x, illustrating that the original and inverse functions are reflections of each other. The process of finding the inverse function is summarized as solving for x in terms of y and then renaming y as x.

Mindmap
Keywords
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. In the context of the video, the function 'f of x' is defined as 'negative x plus 4', and the script discusses finding its inverse, which is a crucial concept in understanding the relationship between inputs and outputs in mathematical functions.
💡Inverse Function
An inverse function is a mathematical concept where for a given function, the inverse 'undoes' the effect of the original function. It's denoted as f^-1(x), and it's found by solving the equation y = f(x) for x in terms of y. The script explains how to find the inverse of the function f(x) = -x + 4 by setting y = f(x) and then solving for x in terms of y, resulting in the inverse function f^-1(x) = -y + 4.
💡Coordinate Plane
The coordinate plane is a two-dimensional, Cartesian coordinate system where each point is defined by an ordered pair (x, y). It is used to graph functions and their properties. The video script refers to graphing the original function and its inverse on the coordinate plane to visually understand their relationship and behavior.
💡Variable
In mathematics, a variable is a symbol, often a letter, that stands for an unknown or variable value. The script uses variables x and y to represent the input and output of functions, respectively. The process of finding the inverse involves switching these roles, solving for x in terms of y and vice versa.
💡Solving for x
Solving for x is the process of manipulating an equation to isolate the variable x on one side of the equation. In the script, this is done to find the inverse function by starting with y = -x + 4 and then solving for x in terms of y, which leads to x = -y + 4.
💡Reflection
In the context of the video, reflection refers to the graphical property where the graph of a function and its inverse are mirror images of each other across the line y = x. The script explains that the function f(x) = -x + 4 is its own inverse and thus its graph is a reflection over the line y = x.
💡Y-intercept
The y-intercept is a point where the graph of a function crosses the y-axis. It occurs when x = 0. The script mentions the y-intercept of the function and its inverse, which is 4 in this case, and explains how it remains the same for both the function and its inverse.
💡Slope
Slope is a measure of the steepness of a line, indicating how much the y-value changes with respect to the x-value. The script discusses the slope of the inverse function, which is -1/2, and how it affects the graph's steepness and direction.
💡Graph
A graph is a visual representation of data, typically with points on a coordinate plane. In mathematics, it is used to represent the set of all points that satisfy a given equation, such as a function. The script involves graphing both the original function and its inverse to illustrate their relationship and properties.
💡Domain and Range
In the context of functions, the domain is the set of all possible input values (x-values), and the range is the set of all possible output values (y-values). The script explains how the domain and range of the original function become the range and domain of the inverse function, respectively.
Highlights

Introduction of the process to find the inverse of a function by setting y equal to f(x).

Explanation of solving for the inverse by rearranging the equation to solve for x in terms of y.

Demonstration of the algebraic steps to isolate x, including subtracting 4 from both sides of the equation.

Multiplication of both sides by -1 to solve for x in terms of y.

Rewriting the equation to express the inverse function in terms of y, then renaming y as x.

Identification of the original function and its inverse as identical, highlighting the unique property of the function being its own inverse.

Graphical representation of the function and its inverse, showing they are the same line on the coordinate plane.

Discussion on the y-intercept of the function and its significance in understanding the function's behavior.

Illustration of the function's reflection over the line y=x, explaining the concept of a function and its inverse being reflections.

Verification of the function being its own inverse through examples of input and output mappings.

Introduction of a second function g(x) = -2x - 1 and the process of finding its inverse.

Algebraic manipulation to solve for x in terms of y for the second function, g(x).

Expression of the inverse function g^(-1)(x) in terms of x, after renaming y as x.

Graphing of the inverse function g^(-1)(x), including its y-intercept and slope.

Visual demonstration of the reflection of g(x) over the line y=x to become its inverse.

General explanation of the process to find the inverse function by algebraically solving for x in terms of y.

Transcripts

Browse More Related Video

Introduction to function inverses | Functions and their graphs | Algebra II | Khan Academy

Function inverses example 3 | Functions and their graphs | Algebra II | Khan Academy

Function inverses example 2 | Functions and their graphs | Algebra II | Khan Academy

Introduction to Inverse Functions

Derivative of Inverse Functions | Calculus 1

Inverse Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Inverse FunctionsAlgebraic MethodsGraphical RepresentationFunction ReflectionMathematics EducationProblem SolvingEducational ContentMath TutorialFunction GraphsInverse Algebra