Most Difficult AP Calculus FRQ Parts (Everyone in AB & BC Should Know)
TLDRThe video script discusses various tricky and unique free-response questions (FRQs) from the AP Calculus exam, which students often find challenging. The instructor shares strategies for tackling these problems, starting with area and volume questions, moving on to differential equations, and then addressing limit, continuity, and differentiability issues. The video also covers related rates and other unusual problems, emphasizing the importance of understanding the underlying concepts and applying them to unique scenarios. The instructor provides detailed explanations and solutions for each problem, encouraging students to review these challenging topics before their exam to ensure they are well-prepared.
Takeaways
- 📚 Start with drawing rectangles and rectangular prisms for area and volume problems, especially when the approach is not immediately clear.
- 🔍 For tricky volume problems, integrate the product of the cross-section's dimensions and depth function to find the total volume.
- 🧮 Use the fundamental theorem of calculus to avoid simplifying numerical answers unnecessarily, especially when dealing with complex integrals.
- 📈 In problems involving differential equations, substitute given solutions into the equation and equate coefficients to solve for unknowns.
- 🤔 For limits, continuity, and differentiability, apply the definitions rigorously, even when one-sided limits are involved.
- 📉 When evaluating functions, ensure you understand the difference between rates in and rates out, and how they apply over different intervals.
- 🔄 Utilize the chain rule for related rates problems by expressing the rate with respect to time as the product of the rate with respect to another variable and the rate of change of that variable with respect to time.
- 📊 Adding auxiliary lines or graphs can help visualize and solve problems, especially when dealing with derivatives and critical points.
- 🔢 Be cautious of piecewise functions and ensure that the correct rate is applied over the specified interval.
- 🔬 In problems with multiple representations (tables, graphs, functions), be prepared for a variety of questions that could span different aspects of calculus.
- 🧐 Always be confident in your understanding of calculus concepts even when faced with unique or unfamiliar problem types; trust your knowledge to guide you through the solution process.
Q & A
What is the main purpose of the video?
-The main purpose of the video is to review tricky, unique, or complex Free Response Questions (FRQs) from the AP Calculus exam that students have historically found challenging.
What topics are covered in the video?
-The video covers topics including area and volume problems, differential equations, limit continuity, differentiability, related rates, and other miscellaneous complex problems.
Why does the instructor suggest drawing rectangles and rectangular prisms for certain problems?
-The instructor suggests drawing rectangles and rectangular prisms to visualize cross-section problems and understand the relationship between the depth of the water (h of x) and the volume to be calculated.
How does the instructor approach the funnel volume problem from 2016?
-The instructor approaches the funnel volume problem by recognizing that the radius is a function of height (r as a function of h) and setting up an integral from 0 to 10, considering the radius and height relationship.
What is the significance of the video mentioning L'Hôpital's rule?
-The video mentions L'Hôpital's rule because it has been a recent emphasis in the AP Calculus exam. The instructor has made a separate video specifically for L'Hôpital's rule application in FRQs.
How does the instructor solve the differential equation problem from 2007?
-The instructor solves the differential equation problem by substituting y with mx + b into the equation, factoring, and then equating coefficients to find the values of m and b.
What is the importance of understanding the definition of continuity in the context of the video?
-Understanding the definition of continuity is important because it is used to solve problems related to limits and differentiability, which are common in AP Calculus FRQs.
How does the instructor handle related rates problems?
-The instructor handles related rates problems by focusing on the given rates and applying the chain rule to find the rate of change with respect to time, as demonstrated in the wind chill and gasoline consumption examples.
What is the strategy for solving the rate in-rate out problem from 2017?
-The strategy is to carefully consider the intervals during which the rates apply, ensuring that the correct intervals are used for each rate when calculating the amount of change.
Why does the instructor emphasize the importance of confidence when facing unique or complex problems?
-The instructor emphasizes confidence because the fundamental calculus concepts required to solve these problems are the same as those used in more straightforward problems. The key is to apply known calculus concepts to the unique context of the problem.
What is the approach for the particle motion problem in 2021?
-The approach involves determining the relative positions and velocities of the particles at a given time, and then analyzing their motion to conclude whether they are moving toward or away from each other.
How does the instructor suggest students prepare for the exam?
-The instructor suggests that students should review and practice a variety of problems, including those that are unique or tricky, to be well-prepared for the exam. They also recommend being familiar with various problem-solving techniques and theorems.
Outlines
📚 Exam Preparation: Tackling Tricky FRQs
The speaker introduces the video's purpose, which is to address the tricky, unique, or weird free-response questions (FRQs) that students have historically found challenging. The strategy involves revisiting these questions after thorough review for a last-minute check. The topics covered include area and volume problems, differential equations, limit and continuity, differentiability, related rates, and a mix of other unusual problems. A separate video is mentioned for l'Hôpital's rule, which is not covered in this session. The focus is on understanding the approach to these problems rather than just the solutions.
🔍 Strategies for Solving Uncommon Problems
The speaker discusses various problem-solving strategies for uncommon problems, such as using one-sided limits, the definition of continuity, and the derivative. Examples include a funnel volume problem, a spinning toy problem, and a problem involving the wind chill. The emphasis is on recognizing the patterns in problems and applying the fundamental theorem of calculus without simplifying the numerical answer unnecessarily. The speaker also highlights the importance of understanding the definition of continuity and differentiability.
🤔 Applying the Squeeze Theorem and Continuity
The speaker addresses the concept of continuity and how it relates to differentiability, particularly focusing on the squeeze theorem. The summary includes a problem where the function k is bounded by two differentiable functions g and h, and the task is to establish the continuity and differentiability of k. The speaker emphasizes the importance of understanding the definitions and applying them correctly to solve the problems.
📉 Related Rates and Chain Rule Application
The speaker delves into related rates problems, which often require the application of the chain rule. Two examples are provided: one involving wind chill calculation and the other concerning the consumption of gasoline in a car. The key is to identify the correct variables and their rates of change, then apply the chain rule to find the rate of change with respect to time. The speaker also encourages rewriting functions in terms of the given variable to simplify the problem.
🧮 Integrating Rates for Total Profit and Snow Removal
The speaker explains how to approach problems that involve integrating rates to find totals, such as calculating profit from the sale of a cable or the amount of snow removed from a driveway. The emphasis is on understanding the context of the integral and how it applies to the problem. The speaker also advises reevaluating answers in the context of the entire problem, especially when parts of the question are interconnected.
📈 Graph Interpretation for Critical Points and Function Behavior
The speaker discusses the importance of graphing functions to understand their behavior, such as finding critical points and intervals of increase or decrease. The summary covers a problem where the graph of the derivative of a function g is given, and the task is to analyze the function h, which is derived from g. The speaker suggests adding relevant lines to the graph for better visualization and understanding of the function's behavior.
🔢 Utilizing the Intermediate Value Theorem and Rate Analysis
The speaker addresses problems that involve the intermediate value theorem and rate analysis, such as finding the time when the rates of change for two different quantities are equal or analyzing the accumulation of snow and its removal. The focus is on understanding the intervals over which rates apply and how to apply the intermediate value theorem to justify the existence of a solution.
📊 Multi-Representation Problems and Confidence in Analysis
The speaker talks about multi-representation problems that include tables, graphs, and functions, which can lead to a variety of questions. The emphasis is on being confident in one's knowledge and understanding of calculus concepts, even when faced with unusual or complex scenarios. The speaker reassures viewers that with a solid grasp of the fundamentals, they can tackle even the most challenging problems.
🤓 Embracing Unique Questions and Applying Calculus
The speaker encourages viewers to approach unique or twist questions with confidence, using their calculus knowledge to understand how to apply standard concepts to new scenarios. An example involving two particles and their relative motion is discussed, highlighting the need to analyze positions and velocities to determine if the particles are moving toward or away from each other. The speaker advises not to be afraid of such questions and to think through them methodically.
Mindmap
Keywords
💡Volume
💡Differential Equations
💡Limits
💡Continuity
💡Differentiability
💡Related Rates
💡Chain Rule
💡L'Hôpital's Rule
💡Integration
💡Critical Points
💡Polar Coordinates
Highlights
The video focuses on addressing tricky or unique Free Response Questions (FRQs) from the AP Calculus exam.
Students often find these specific FRQs challenging, which are reviewed annually for their complexity.
The presenter discusses strategies for tackling area, volume, and differential equation problems that students typically find difficult.
A separate video is available for using L'Hôpital's rule in FRQs, emphasizing its recent importance in exams.
The video includes a walkthrough of a 2008 exam problem involving the volume of water in a pond with a unique cross-section.
The presenter uses the method of drawing rectangles and rectangular prisms to solve cross-section area problems.
For a 2016 funnel volume problem, the presenter clarifies misconceptions about the given function's graph, emphasizing the importance of understanding the problem's visual representation.
A 2021 spinning toy problem is discussed, where the volume of the toy is given, and the value of a constant 'c' needs to be determined.
The video explores a 2007 differential equation problem, offering two different methods to find the values of 'm' and 'b'.
The presenter emphasizes the importance of recognizing patterns across various FRQs to solve them efficiently.
Limit, continuity, and differentiability are covered with a focus on uncommon problems that may appear on the exam.
The use of one-sided limits and the definition of the derivative is demonstrated using a 2009 problem as an example.
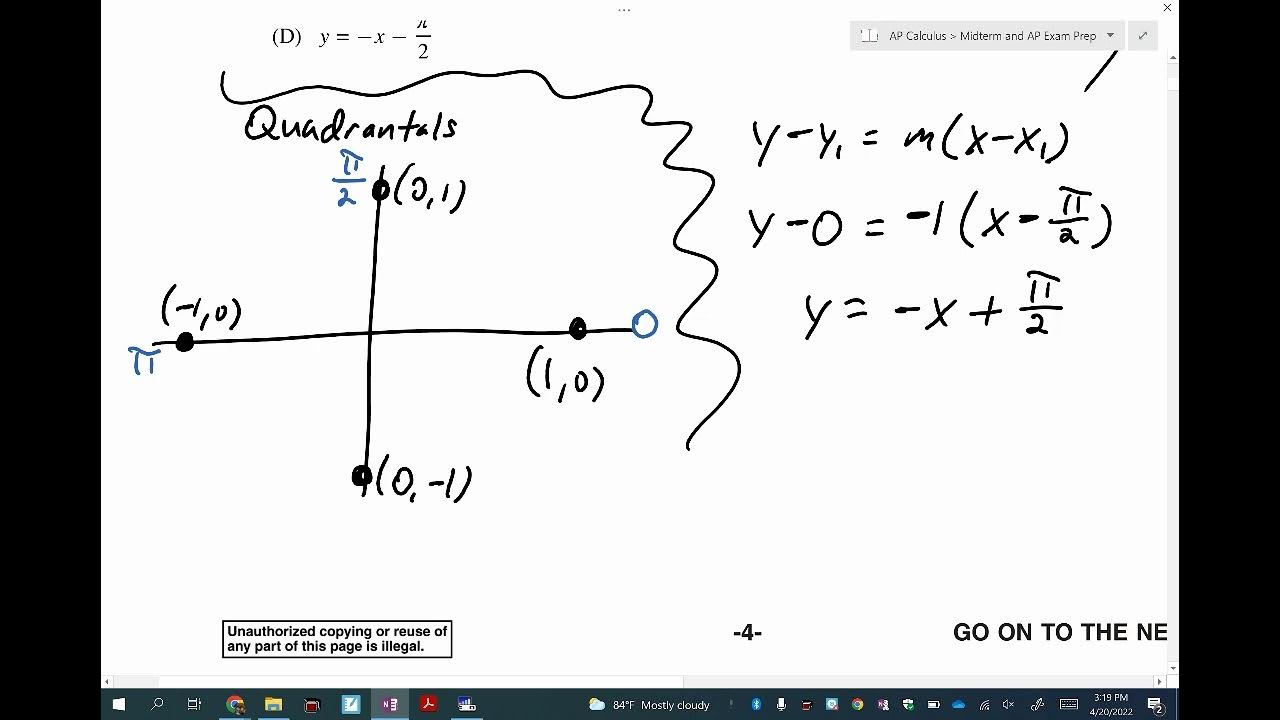
The concept of continuity is applied to determine if a function is continuous at a given point using a 2011 problem.
The presenter discusses the squeeze theorem and its application in a 2020 problem, without explicitly naming the theorem.
Related rates problems are tackled, such as a wind chill calculation and a car's fuel consumption, using the chain rule.
The video points out that less familiar concepts are often explained in detail within the problem, guiding students on how to approach them.
Profit maximization in a sales context is explored through integration of rates, as demonstrated in a 2009 cable sale problem.
The presenter advises on not underthinking or overthinking problems, using a 2010 snow removal problem as an example.
The importance of understanding the intervals over which rates apply is highlighted using a 2017 banana display problem.
The video concludes with a discussion on a 2021 problem involving the movement of particles, encouraging students to apply their calculus knowledge to new and unique scenarios.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: