2021 Live Review 5 | AP Calculus BC | Examining Differential Equations & Logistics
TLDRIn this engaging AP Calculus BC exam prep session, the focus is on mastering differential equations, particularly logistic differential equations and their applications. The video covers the general forms of logistic differential equations, the concept of carrying capacity, and the inflection point where the growth rate is at its peak. Through illustrative examples, the instructors guide students on how to tackle rate problems, emphasizing the importance of understanding the context and applying calculus concepts effectively. The session also addresses common misconceptions and provides strategies for tackling free-response and multiple-choice questions, aiming to boost students' confidence and performance in the upcoming exam.
Takeaways
- 📘 The session focuses on AP Calculus BC exam prep, specifically on differential equations and logistic growth models.
- 🔢 The logistic differential equation is a key topic for the AP Calculus BC exam, with two common forms that students must memorize.
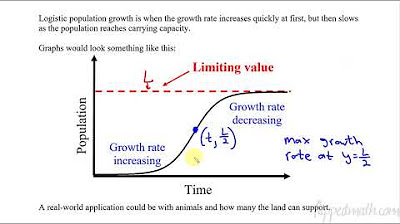
- 📈 The carrying capacity (L) in logistic models represents the maximum population size that can be sustained indefinitely.
- 📊 The growth rate of a logistic model is fastest at half the carrying capacity (L/2) and slows down as it approaches L.
- 📚 The general form of the logistic differential equation involves the variable y and is either of the forms: dy/dt = ky(1-y/L) or dy/dx = ky(1-y/L)^2.
- 🤝 The instructors, Brian and Tony, provide a collaborative approach to teaching, with Tony focusing on the conceptual understanding and Brian on the practical application.
- 📊 The session includes examples of how to apply the logistic model to real-world scenarios, such as the number of AP Calculus exam responses uploaded over time.
- 📝 Students are encouraged to take screenshots of key slides for quick reference and to understand the properties of logistic functions for effective exam preparation.
- 📈 The concept of concavity and the point of inflection are crucial in understanding the behavior of logistic growth curves.
- 📊 The session emphasizes the importance of sketching solution curves for differential equations, especially for paper-based AP exam formats.
- 🎯 The instructors provide strategies for tackling free-response questions, including using initial conditions to solve for constants in differential equations.
Q & A
What is the main focus of the video in terms of AP Calculus BC exam preparation?
-The main focus of the video is to discuss differential equations, specifically logistic differential equations and logistic curves, which are high-leverage topics for the AP Calculus BC exam.
What are the two general forms of the logistic differential equation mentioned in the video?
-The two general forms of the logistic differential equation are: dy/dt = k*y*(L - y) and dy/dt = k*(L - y)*y/L, where k represents the growth rate and L is the carrying capacity.
What is the significance of the carrying capacity (L) in logistic growth models?
-The carrying capacity (L) represents the maximum population size or limit that the environment can sustain indefinitely. It is a key parameter in logistic growth models, determining the upper bound of growth.
How does the growth rate change at the halfway point of the carrying capacity in a logistic model?
-At the halfway point of the carrying capacity, the growth rate is at its maximum. Beyond this point, the growth rate decreases as the population size approaches the carrying capacity.
What is the relationship between the second derivative and the concavity of the logistic growth curve?
-If the second derivative is positive, the curve is concave up and the growth rate is increasing. If the second derivative is negative, the curve is concave down and the growth rate is decreasing.
How does the video prepare students for the AP Calculus BC exam?
-The video prepares students by reviewing key concepts and formulas related to logistic growth models, providing strategies for solving exam problems, and offering practice with free-response questions that simulate the exam format.
What is the example scenario used in the video to illustrate logistic growth?
-The example scenario used in the video is the total number of AP Calculus exam responses uploaded after the testing is completed, with the number of responses modeled by a logistic function.
What is the significance of the tangent line approximation in the video?
-The tangent line approximation is used to estimate the rate of change at a specific point, which can be useful for predicting future values or understanding the behavior of a function at a particular time.
What is the role of the logistic differential equation in solving real-world problems as discussed in the video?
-The logistic differential equation is used to model situations where growth is limited by a carrying capacity, such as population growth, spread of rumors, or the filling of a parking garage, as illustrated in the video examples.
What advice does the video give for tackling free-response questions on the AP Calculus BC exam?
-The video advises students to be familiar with the general forms of logistic differential equations, understand the properties of logistic growth such as carrying capacity and maximum growth rate, and apply these concepts to solve problems that may appear on the exam.
Outlines
📚 Starting AP Calculus BC Exam Prep - Week Two
The video begins with an introduction to the second week of AP Calculus BC exam preparation for the 2021 exam. The speaker recaps the topics covered in the previous week, including Taylor series, polar graphs, parametrics, and integration techniques. This week, the focus is on completing major topics with four more videos that aim to boost exam scores. The speaker emphasizes the importance of understanding differential equations, specifically logistic differential equations and logistic curves, which are consistently on the exam. The goal is to ensure that viewers achieve a perfect score on the exam, building on the hard work put in throughout the year.
📈 Discussing Differential Equations and Logistic Growth
The speaker delves into the specifics of differential equations, particularly logistic differential equations, and their significance in the AP Calculus exam. The discussion includes the general form of the logistic differential equation and the two legitimate forms it can take. The concept of carrying capacity, the maximum population size in a given environment, is introduced, drawing parallels with AP Biology. The speaker also explains the fastest growth rate and its relation to the carrying capacity. The segment concludes with an example involving the total number of AP Calculus responses uploaded after the exam, using this scenario to illustrate the application of logistic equations.
🔢 Solving Tangent Line Problems and Logistic Equations
This paragraph focuses on solving problems related to the tangent line approximation and logistic equations. The speaker provides a step-by-step guide on writing the equation of a tangent line, emphasizing the need for a slope and a point. The example given involves the number of AP Calculus responses uploaded as a function of time. The speaker then transitions to discussing logistic equations, highlighting the rate of change in relation to the carrying capacity and how to determine if the rate of responses is increasing or decreasing at a specific time. The explanation includes visualizing the logistic curve and understanding its concavity to solve the problem without calculus.
🚗 Modeling Car Exits with Differential Equations
The speaker presents a problem involving a parking garage and the number of cars exiting over time, modeled by a differential equation. The task is to sketch the solution curve for the given differential equation, taking into account the initial condition of 435 cars in the garage at time zero. The speaker emphasizes the importance of the solution curve passing through the origin and being continuous. The solution curve is then used to find the particular solution to the differential equation, with the speaker guiding viewers through the process of separation of variables and integration. The initial condition is applied to find the constant of integration, leading to the final form of the solution.
📊 Applying the Logistic Model to Real-World Scenarios
The speaker applies the logistic model to a real-world scenario, using the context of a parking garage to illustrate how the model works. The problem involves finding the number of cars in the garage at a specific time, given the rate at which cars enter and exit. The speaker demonstrates how to use the previously derived logistic equation to calculate the number of cars in the garage at time 15, incorporating the rate of car entries and exits. The solution involves integrating the rate of entry and subtracting the number of cars that have exited, resulting in the total number of cars in the garage at the given time. The speaker also addresses the importance of understanding the properties of logistic functions, such as the carrying capacity and the point of inflection, which are crucial for solving exam questions efficiently.
🎓 Final Tips and Strategies for Differential Equations
The speaker concludes the video with final tips and strategies for tackling differential equations, particularly logistic equations, on the AP Calculus exam. The emphasis is on understanding the context of the problem, recognizing the forms of logistic differential equations, and knowing the properties of logistic growth, such as the carrying capacity and the fastest growth rate. The speaker encourages viewers to be confident in their abilities and to keep pushing hard in their exam preparation. The video ends with a preview of the next topic, which is convergence tests for series, and the speakers express their support and confidence in the viewers' success in the upcoming AP Calculus exam.
Mindmap
Keywords
💡AP Calculus BC
💡Differential Equations
💡Logistic Growth Models
💡Taylor Series
💡Carrying Capacity
💡Point of Inflection
💡Partial Fraction Decomposition
💡Free Response Questions (FRQs)
💡L'Hôpital's Rule
💡Convergence Tests
Highlights
The session is focused on AP Calculus BC exam preparation, specifically addressing high leverage topics for the 2021 exam.
Last week's session covered Taylor series, polar graphs, parametrics, and integration techniques.
This week's focus is on differential equations, particularly logistic differential equations and logistic curves, which are consistently on the Calc BC exam.
The instructors aim to provide strategies and insights to help students achieve a perfect score on the exam.
The general form of the logistic differential equation is introduced, with two legitimate forms that may appear on the exam.
The concept of carrying capacity is explained, relating to the maximum population limit in a given environment, which is a key idea in AP Bio and Calculus.
The fastest growth rate of a logistic model is discussed, which occurs at half the carrying capacity.
The second derivative of the population curve is analyzed to understand the concavity and inflection points of the logistic curve.
An example involving the total number of AP Calculus responses uploaded after the exam is used to illustrate the application of tangent lines and approximations.
The logistic equation model is applied to a real-world scenario of cars exiting a parking garage, demonstrating the practical use of mathematical models.
The solution curve for a differential equation is sketched, emphasizing the importance of continuity and the function's domain.
The separation of variables technique is used to find the particular solution to a differential equation.
The initial condition is utilized to find the constant of integration in the solution to a differential equation.
A comprehensive approach to solving free response questions on the AP Calculus exam is presented, combining multiple concepts from calculus.
The session concludes with a reminder that understanding the properties of logistic functions can save time during the exam and help students earn more points.
The instructors encourage students to keep pushing hard and believe in their abilities to succeed in the AP Calculus exam.
Transcripts
Browse More Related Video

2022 Live Review 2 | AP Calculus BC | Euler's Method, Logistics, and Differential Equations
Calculus BC – 7.9 Logistic Models with Differential Equations

AP Calculus Practice Exam Part 3 (MC #21-30)

1 | MCQ | Practice Sessions | AP Calculus BC

AP Calculus AB/BC Unit 7 Practice Test

AP Calculus BC Lesson 7.9
5.0 / 5 (0 votes)
Thanks for rating: