Math 1325 Lecture 9 5 - Product & Quotient Rule

Michael Bailey
9 May 201614:10
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses two fundamental rules in calculus: the product rule and the quotient rule. The product rule is introduced as a shortcut for differentiating a function that is a product of two differentiable functions, u(x) and v(x). It is expressed as the derivative of f(x) being the first function times the derivative of the second plus the second function times the derivative of the first. The quotient rule is more complex and is used for differentiating a function that is a quotient of two functions. It is articulated as the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all divided by the denominator squared. The script provides examples of applying these rules to polynomials and emphasizes the importance of practicing these rules for better understanding. It also touches on the concept of marginal revenue, explaining it as the revenue for selling an additional item and how it is calculated using derivatives. The script concludes with a reminder that marginal calculations are estimates rather than exact figures.

Takeaways
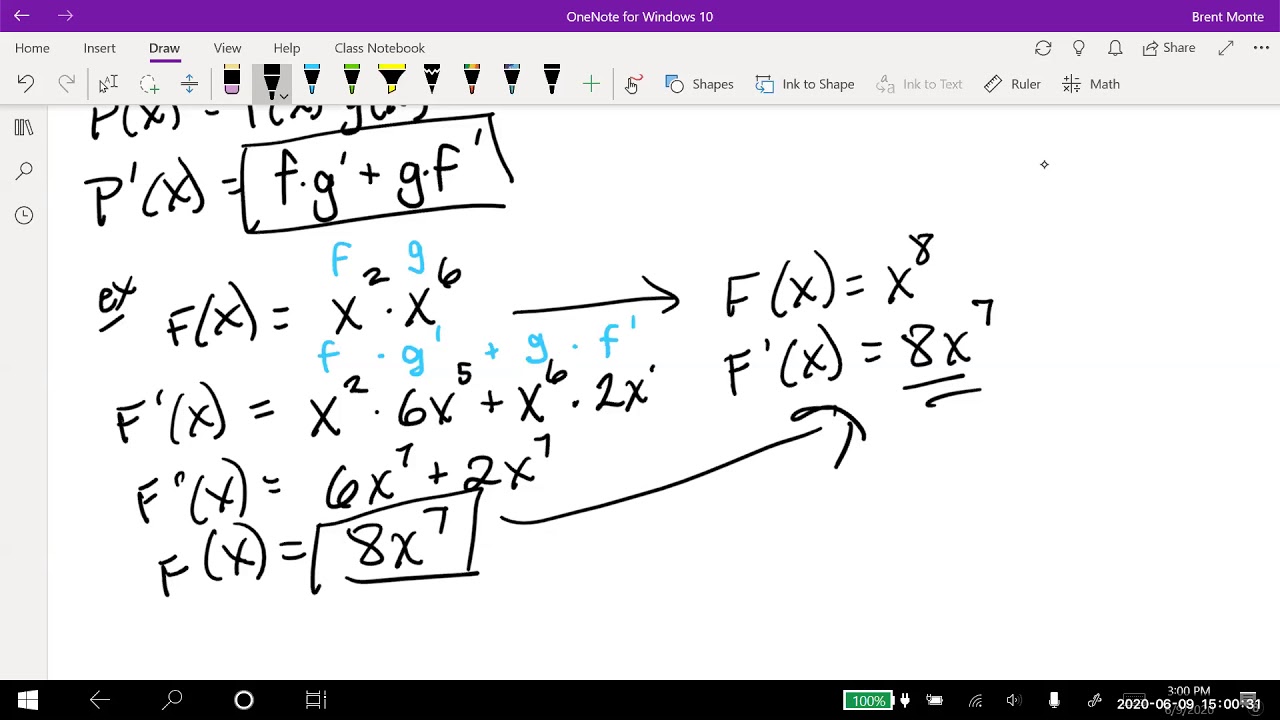
  • 📚 The Product Rule is a shortcut for finding the derivative of a function that is a product of two differentiable functions, u(x) and v(x). It states that the derivative of f(x) = u(x)v(x) is u'(x)v(x) + u(x)v'(x).
  • 📈 To apply the Product Rule, first find the derivative of each individual function and then apply the rule to get the derivative of their product.
  • 🔢 For polynomials, the derivative can be found by applying the power rule and then using the distributive property to combine terms.
  • 📌 The Quotient Rule is used for finding the derivative of a function that is a quotient of two differentiable functions. It is not as simple as taking the derivative of the numerator and denominator separately.
  • ⚖️ The Quotient Rule formula is given as f'(x) = (v(x) * u'(x) - u(x) * v'(x)) / v(x)^2, where f(x) = u(x) / v(x).
  • 🧮 When applying the Quotient Rule, it's important to remember to square the denominator in the formula.
  • 📐 The derivative of a function at a specific point gives the slope of the tangent line at that point.
  • 💡 Practicing the application of both the Product and Quotient Rules will help to overcome initial confusion and make the process more intuitive.
  • 🧮 For word problems involving revenue, the derivative of the revenue function gives the marginal revenue, which estimates the revenue from selling an additional item.
  • 💰 Marginal revenue calculations are estimates and should be interpreted in the context of the problem, such as revenue per unit sold.
  • 📋 When calculating marginal revenue at a specific quantity, plug in the value for x into the derivative function and solve.
  • 📝 It's important to express the final answer in a way that makes sense in the context of the problem, such as using currency notation for revenue.
Q & A

  • What is the product rule for derivatives?

    -The product rule is a shortcut for finding the derivative of a function that is a product of two differentiable functions, u(x) and v(x). It states that the derivative of f(x) = u(x)v(x) is given by f'(x) = u'(x)v(x) + u(x)v'(x), where u'(x) and v'(x) are the derivatives of u(x) and v(x) respectively.

  • How does the product rule apply to polynomial functions?

    -The product rule applies to polynomial functions by breaking down the polynomial into two factors, identifying the derivatives of each factor, and then applying the rule to find the derivative of the product. For example, if you have (2x^3 + 3x + 1)(x^2 + 4), you would find the derivative of each polynomial and then apply the product rule to get the derivative of the entire expression.

  • What is the quotient rule for derivatives?

    -The quotient rule is used to find the derivative of a function that is a quotient of two differentiable functions, u(x) and v(x). It states that the derivative of f(x) = u(x)/v(x) is given by f'(x) = (v(x)u'(x) - u(x)v'(x)) / (v(x))^2, where u'(x) and v'(x) are the derivatives of u(x) and v(x) respectively.

  • How do you find the slope of the tangent line at a specific point using derivatives?

    -To find the slope of the tangent line at a specific point using derivatives, you first find the derivative of the function, which represents the slope of the tangent line at any point on the function. Then, you substitute the x-coordinate of the specific point into the derivative to find the exact slope at that point.

  • What is the significance of marginal revenue in business?

    -Marginal revenue is the additional revenue that a company receives from selling one more unit of a product. It is significant in business as it helps in understanding the potential revenue gain from selling an additional unit, which is crucial for making decisions about production levels and pricing strategies.

  • How is the marginal revenue calculated?

    -Marginal revenue is calculated by taking the derivative of the revenue function. This derivative represents the rate of change of revenue with respect to the quantity of goods sold, and it gives the additional revenue generated from selling one more unit.

  • What is the difference between the product rule and the quotient rule in calculus?

    -The product rule is used when you have a function that is a product of two other functions, and it involves multiplying the first function by the derivative of the second and adding it to the second function times the derivative of the first. The quotient rule, on the other hand, is used for a function that is a quotient of two other functions, and it involves a more complex formula that includes the denominator squared and a subtraction.

  • How do you simplify the derivative of a quotient like x^3/x?

    -To simplify the derivative of a quotient like x^3/x, you can first simplify the quotient itself by canceling out common factors. In this case, x^3/x simplifies to x^2. Then, you can find the derivative of x^2, which is 2x, using the power rule.

  • What is the purpose of practicing derivative rules like the product and quotient rules?

    -Practicing derivative rules like the product and quotient rules helps to internalize the formulas and improve problem-solving skills. It makes it easier to apply these rules to more complex functions and to solve real-world problems that involve rates of change, such as those in physics, engineering, and economics.

  • Why is it important to remember the formulas for the product and quotient rules?

    -It is important to remember the formulas for the product and quotient rules because they are fundamental to calculus and are used frequently in various mathematical and real-world applications. Being able to recall these formulas accurately allows for efficient problem-solving and understanding of more advanced concepts.

  • What is the role of the derivative in finding the instantaneous rate of change?

    -The derivative of a function at a particular point gives the instantaneous rate of change of the function at that point. It represents the slope of the tangent line to the graph of the function at that point, which is the best linear approximation of the function's rate of change near that point.

  • How do you apply the quotient rule to find the derivative of a function like y = 1/(x^3)?

    -To apply the quotient rule to find the derivative of y = 1/(x^3), you would let u(x) = 1 and v(x) = x^3. Then you would find u'(x) = 0 and v'(x) = 3x^2. Plugging these into the quotient rule formula, you would get y' = (v(x)u'(x) - u(x)v'(x)) / (v(x))^2, which simplifies to -3x^2 / (x^6), and further simplifies to -3 / (x^4).

Outlines
00:00
📚 Understanding the Product Rule for Derivatives

This paragraph introduces the concept of the product rule in calculus. It explains that when you have a function composed as a product of two differentiable functions, U(X) and V(X), the derivative of the function f(X) is found by adding the product of the first function and the derivative of the second to the product of the second function and the derivative of the first. The paragraph clarifies that this rule can seem confusing at first but becomes straightforward with practice. It then provides an example involving polynomials to illustrate the application of the product rule and demonstrates how to calculate the derivative of a product of functions.

05:01
🔍 Applying the Quotient Rule for Derivatives

The second paragraph delves into the quotient rule, which is a method for finding the derivative of a function that is the quotient of two other functions, U(X)/V(X). It emphasizes that simply taking the derivative of the numerator and denominator does not yield the correct result and instead, the quotient rule must be applied. The quotient rule is presented as the derivative of the function being the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. The paragraph also provides an example to illustrate the application of the quotient rule and discusses the importance of practicing the rule for better understanding.

10:10
📈 Calculating Marginal Revenue and Applying Derivatives in Economics

The third paragraph discusses the application of derivatives in economics, particularly in calculating marginal revenue. It explains that marginal revenue is the additional revenue generated from selling one more unit of a product. The paragraph outlines how to find the marginal revenue function by taking the derivative of the revenue function and then uses this function to find the marginal revenue at a specific quantity, in this case, when x equals fifteen. It also touches on the concept of marginal calculations in economics, noting that they are estimates rather than exact figures. The paragraph concludes with an example calculation of marginal revenue, emphasizing the importance of context in interpreting the results.

Mindmap
Keywords
💡Product Rule
The product rule is a fundamental principle in calculus used to find the derivative of a product of two functions. It states that the derivative of a function which is a product of two differentiable functions (u(x) and v(x)) is equal to the first function times the derivative of the second plus the second function times the derivative of the first. In the video, the product rule is applied to polynomial functions to demonstrate how to calculate their derivatives, which is central to understanding the rate of change of these functions.
💡Quotient Rule
The quotient rule is a mathematical rule used to find the derivative of a quotient of two functions. It is given as the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. This rule is crucial when dealing with fractions in calculus, and it is demonstrated in the video by applying it to various functions to find their derivatives, emphasizing its importance in differentiating quotients accurately.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. It is a fundamental concept used to analyze the behavior of functions, such as their slope at a particular point or their increasing/decreasing nature. In the video, the process of finding derivatives is central to understanding how the product and quotient rules are applied to specific functions, like polynomials and revenue functions.
💡Differentiable Functions
Differentiable functions are those for which a derivative exists at every point in their domain. This means that the functions have a well-defined rate of change at every point. The video emphasizes that both the product and quotient rules require the functions involved (u(x) and v(x)) to be differentiable for the rules to be applicable.
💡Polynomials
Polynomials are algebraic expressions involving a sum of terms, each term consisting of a variable raised to a non-negative integer power, multiplied by a coefficient. In the video, polynomials are used as examples to illustrate the application of the product and quotient rules. They are fundamental in calculus as they are simple yet versatile functions for demonstrating various concepts.
💡Marginal Revenue
Marginal revenue refers to the additional revenue that a company receives from selling one more unit of a product. It is calculated by taking the derivative of the revenue function. In the context of the video, the concept of marginal revenue is used to illustrate how derivatives can be applied in economics to estimate the revenue from selling an additional item, such as the sixteenth flash drive in the example provided.
💡Power Rule
The power rule is a basic rule in calculus that allows for the differentiation of a function raised to a power. It states that the derivative of x^n (where n is a constant) is n*x^(n-1). The video uses the power rule to simplify the derivative of x^3/x, which is an application of the quotient rule, by reducing it to the simpler form of x^2 and then applying the power rule.
💡Slope of the Tangent
The slope of the tangent to a curve at a particular point is equal to the derivative of the function at that point. It represents the instantaneous rate of change of the function. In the video, the concept is used to find the slope of the tangent line at specific points on a curve, which is another application of derivatives in understanding the behavior of functions.
💡Instantaneous Rate of Change
The instantaneous rate of change is the rate at which a quantity changes at a specific instant. In calculus, it is synonymous with the derivative of a function at a particular point. The video discusses finding the instantaneous rate of change using derivatives, which is a key concept in analyzing the behavior of functions at specific points.
💡Marginal Cost and Profit
Marginal cost is the cost of producing one additional unit of a good or service, while marginal profit is the additional profit gained from selling one more unit. The video touches on these concepts in the context of economic analysis, emphasizing that derivatives are used to calculate these marginal values by differentiating the cost or profit functions.
💡FOIL Method
The FOIL method is a technique used to multiply two binomials (expressions with two terms). It stands for First, Outer, Inner, Last, and it helps to ensure that each term is multiplied correctly. In the video, the FOIL method is mentioned in the context of expanding expressions when applying the product and quotient rules, which is a common step in finding derivatives.
Highlights

Introduction to the product rule for derivatives, which is a shortcut for finding the derivative of a function that is a product of two differentiable functions.

The product rule states that the derivative of a product of two functions is the first function times the derivative of the second plus the second function times the derivative of the first.

Demonstration of applying the product rule to polynomial functions, including the steps of taking derivatives and multiplying out terms.

Example of finding the slope of the tangent at a specific point using the product rule, which simplifies the process by plugging in the value of x.

Introduction to the quotient rule for derivatives, which is more complex and requires careful application.

The quotient rule formula is presented, emphasizing the importance of memorizing it for tests.

Explanation that the quotient rule involves the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.

Application of the quotient rule to a simplified function, showing that it yields the same result as direct simplification.

Practice problems are provided for the audience to apply the quotient rule to more complex functions.

Solution of a quotient rule problem involving a function with a value, emphasizing the use of the formula and plugging in the value.

Explanation of the instantaneous rate of change and its relation to the derivative, with an example of how to find it using the quotient rule.

Clarification on the concept of marginal revenue, its calculation, and its practical application in estimating revenue from the sale of additional items.

Demonstration of finding the marginal revenue function by taking the derivative of the revenue function.

Procedure for calculating marginal revenue at a specific quantity, emphasizing the context of revenue as a monetary function.

The importance of accurate representation of monetary values in word problems, suggesting the use of currency symbols and units.

Summary of the key takeaways from the transcript, including the application of product and quotient rules, and the concept of marginal revenue.

Transcripts

Browse More Related Video

Product Rule For Derivatives

Product Rule for Derivatives

Taking the derivative of two binomials using product and chain rule

Quotient rule from product & chain rules | Derivative rules | AP Calculus AB | Khan Academy

Simplifying Derivatives

The Quotient Rule for Derivatives — Topic 58 of Machine Learning Foundations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusProduct RuleQuotient RuleDerivativesMath ShortcutsDifferentiationPolynomialsTangent SlopeMarginal RevenueEconomic ConceptsMathematical AnalysisEducational Content