Focal Length of Eyepiece in a Microscope | Physics with Professor Matt Anderson | M28-22

Physics with Professor Matt Anderson
19 Mar 202204:27
EducationalLearning
32 Likes 10 Comments

TLDRThe script discusses a compound microscope's magnification calculation, aiming to achieve a total magnification of 240 with minimum eye strain for a person with a near point of 25 centimeters. Given the barrel length of 18 centimeters and the objective lens focal length of 8 millimeters, the focal length of the eyepiece is derived through a formula. The process involves adjusting variables and solving for the eyepiece's focal length, which is calculated to be 2.3 centimeters, providing a practical approach to understanding microscope magnification.

Takeaways
  • 🔬 The script discusses a question related to the magnification of a compound microscope.
  • 📏 It mentions a microscope with an 18-centimeter long barrel and an objective lens with an 8-millimeter focal length.
  • 🔍 The goal is to find the focal length of the eyepiece to achieve a total magnification of 240.
  • 👀 The microscope is adjusted for minimum eye strain for a person with a near point of 25 centimeters.
  • 🧠 The magnification formula discussed is \( l \times 25 \text{ cm} \) over the focal length of the objective times the focal length of the eyepiece.
  • 📐 The equation is rearranged to solve for the eyepiece's focal length, ignoring the negative sign for inversion.
  • 🔢 Given values are: \( l = 0.18 \) meters, near point = 0.25 meters, \( m = 240 \), and \( f_o = 0.008 \) meters.
  • 📘 The formula to calculate the eyepiece's focal length is \( \frac{l \times 0.25}{m \times f_o} \).
  • 🧮 After plugging in the numbers, the calculated focal length of the eyepiece is 2.3 centimeters.
  • 📝 The result is verified by asking if anyone else got the same answer, ensuring accuracy.
  • 🎶 Background music is playing during the explanation, indicating an informal or casual educational setting.
Q & A

  • What is the main topic discussed in the script?

    -The main topic discussed in the script is the calculation of the focal length of the eyepiece of a compound microscope to achieve a specific total magnification while minimizing eye strain.

  • What is the total magnification required for the microscope in the script?

    -The total magnification required for the microscope is 240 times.

  • What is the length of the microscope barrel mentioned in the script?

    -The length of the microscope barrel is 18 centimeters.

  • What is the focal length of the objective lens in the script?

    -The focal length of the objective lens is 8 millimeters.

  • What is the near point of a person mentioned in the script, and how does it relate to the calculation?

    -The near point of a person is 25 centimeters. It is used in the calculation to determine the focal length of the eyepiece that would cause minimum eye strain.

  • What is the formula used to calculate the magnification of a microscope?

    -The formula used to calculate the magnification of a microscope is \( \frac{L \times 25}{f_o \times f_e} = M \), where \( L \) is the barrel length, 25 is the near point in centimeters, \( f_o \) is the focal length of the objective, \( f_e \) is the focal length of the eyepiece, and \( M \) is the total magnification.

  • How is the focal length of the eyepiece calculated in the script?

    -The focal length of the eyepiece is calculated by rearranging the magnification formula to solve for \( f_e \): \( f_e = \frac{L \times 25}{M \times f_o} \).

  • What is the calculated focal length of the eyepiece in the script?

    -The calculated focal length of the eyepiece is 2.3 centimeters.

  • Why is the negative sign ignored in the calculation of the eyepiece's focal length?

    -The negative sign is ignored because the calculation is only concerned with the magnitude of the focal length, not the direction of the image inversion.

  • What does the script imply about the importance of the eyepiece's focal length in relation to eye strain?

    -The script implies that selecting the correct focal length of the eyepiece is crucial for minimizing eye strain when using the microscope.

  • What unit conversion is performed in the script during the calculation?

    -The unit conversion performed in the script is converting the barrel length from centimeters to meters and the focal length of the objective from millimeters to meters for the calculation.

Outlines
00:00
🔬 Microscope Magnification Calculation

The script discusses a problem related to calculating the focal length of an eyepiece for a compound microscope to achieve a total magnification of 240 with minimum eye strain. Given the microscope's barrel length of 18 centimeters, an objective lens focal length of 8 millimeters, and a person's near point of 25 centimeters, the script explains the magnification formula \( \frac{l \times d}{f_o \times f_e} \), where \( l \) is the barrel length, \( d \) is the near point distance, \( f_o \) is the objective lens focal length, and \( f_e \) is the eyepiece focal length. The script guides through solving for \( f_e \) by rearranging the formula and substituting the given values, resulting in an eyepiece focal length of 2.3 centimeters.

Mindmap
Keywords
💡Microscope
A microscope is an instrument used to observe objects that are too small to be seen by the naked eye. In the video, the focus is on a compound microscope, which uses multiple lenses to magnify the specimen. The script discusses the calculation of the magnification of a microscope, which is central to understanding how the device works and its applications in scientific research.
💡Objective Lens
The objective lens is the lens closest to the specimen in a microscope. It is responsible for the initial magnification of the object being observed. In the script, the focal length of the objective lens is given as 8 millimeters, which is a critical piece of information for calculating the total magnification of the microscope.
💡Focal Length
Focal length is the distance from the center of a lens to the point where it focuses light to form a sharp image. In the context of the video, the focal lengths of both the objective lens and the eyepiece are discussed. The focal length of the eyepiece is unknown and needs to be calculated to achieve the desired magnification.
💡Eyepiece
The eyepiece, also known as the ocular lens, is the lens through which the observer looks to see the magnified image. The script involves a calculation to determine the focal length of the eyepiece required to achieve a specific total magnification of the microscope.
💡Magnification
Magnification refers to the process of making an object or an image appear larger than it is. In the video, the total magnification of the microscope is given as 240 times, and the script discusses how this is calculated based on the focal lengths of the lenses and the length of the microscope barrel.
💡Near Point
The near point is the closest distance at which a person can see an object clearly with the naked eye. In the script, it is mentioned that the calculation is adjusted for minimum eye strain for a person with a near point of 25 centimeters, which is a consideration in the design and use of the microscope.
💡Minimum Eye Strain
Minimum eye strain refers to the condition where the least amount of effort or discomfort is experienced by the eyes when viewing an object. The script mentions adjusting the microscope for minimum eye strain, which is an important consideration for user comfort and prolonged use.
💡Lens
A lens is a usually transparent piece of material, such as glass, that is shaped to focus or disperse light. In the video, the discussion revolves around the lenses of the microscope, specifically the objective lens and the eyepiece, and how their focal lengths contribute to the overall magnification.
💡Calculation
Calculation in this context refers to the mathematical process of determining an unknown value, such as the focal length of the eyepiece, based on known quantities. The script provides a step-by-step guide on how to perform this calculation, which is essential for understanding the principles of microscope magnification.
💡Image Inversion
Image inversion is when an image is flipped upside down or left to right. The script briefly mentions that the image formed by the microscope is inverted but clarifies that this is not a concern for the calculation of magnification, which is the main focus of the video.
💡SI Units
SI units, or International System of Units, is the modern form of the metric system and is the most widely used system of measurement. The script specifies that the calculation should be kept in SI units, which means using meters for the focal lengths and the length of the microscope barrel.
Highlights

The compound microscope has an 18 cm long barrel.

The objective lens has a focal length of 8 mm.

The goal is to find the focal length of the eyepiece for a total magnification of 240.

The microscope is adjusted for minimum eye strain for persons with a near point of 25 cm.

The magnification formula is L * 25 cm / (focal length of objective * focal length of eyepiece).

The image is inverted but this does not affect the magnification calculation.

The magnification M is given as 240.

The barrel length L is 18 cm or 0.18 meters.

The near point distance is 25 cm or 0.25 meters.

The objective lens focal length is 8 mm or 0.008 meters.

The equation to solve for the eyepiece focal length is L * 0.25 / (M * focal length of objective).

Solving the equation gives the eyepiece focal length as 2.3 * 10^-2 meters or 2.3 cm.

The calculation ignores the negative sign, focusing only on the magnitude of the focal length.

Verification of the calculated eyepiece focal length is sought among the participants.

The calculated focal length of 2.3 cm is confirmed as one of the correct answers.

The process demonstrates a step-by-step approach to solving for the eyepiece focal length in a microscope.

The method involves using the given magnification, barrel length, near point distance, and objective lens focal length.

Transcripts

Browse More Related Video

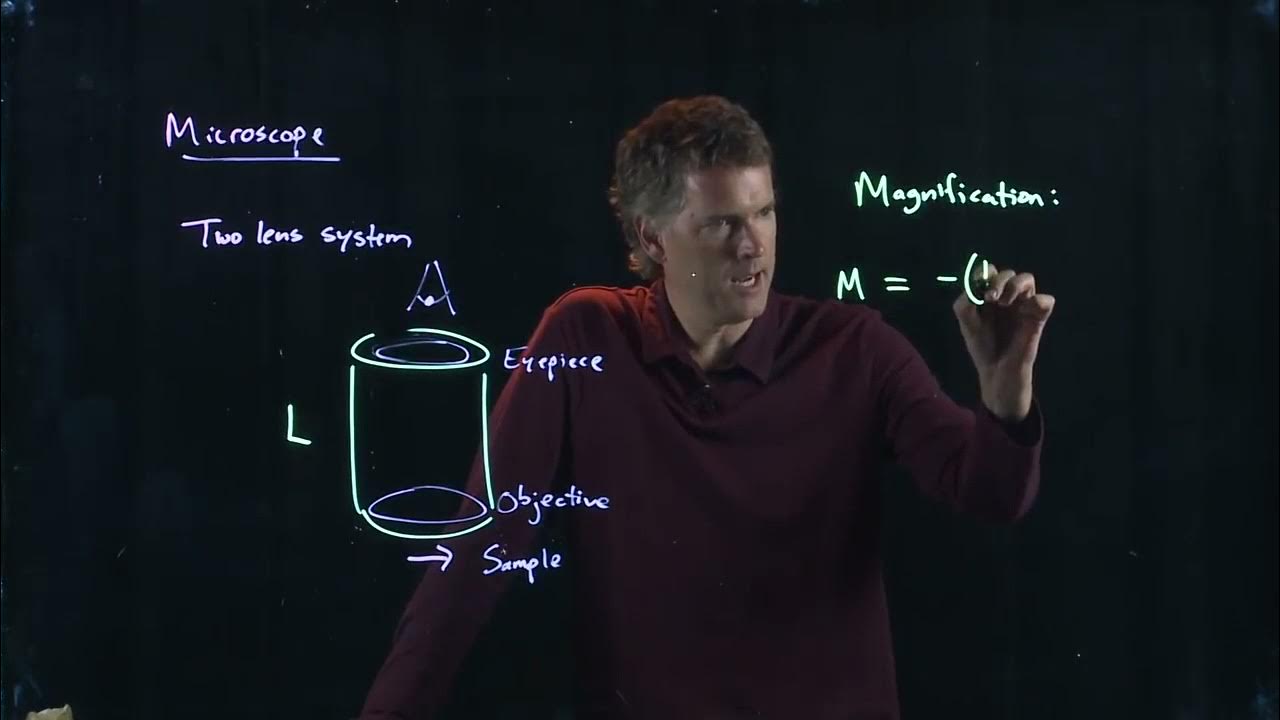
The Microscope | Physics with Professor Matt Anderson | M28-12

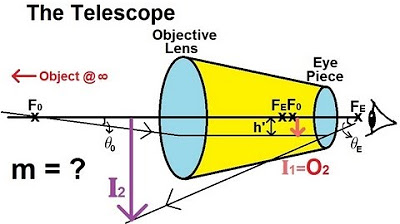
Physics 59 Optical Instruments (2 of 20) The Telescope

The Telescope | Physics with Professor Matt Anderson | M28-13

Physics 59 Optical Instruments (3 of 20) The Microscope

Power of accommodation of the Human Eye | Letstute

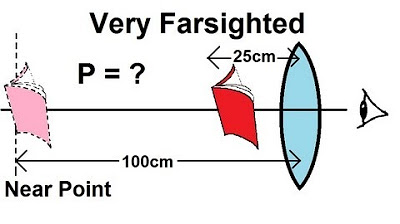
Physics - Optics: Vision Correction (5 of 5) Very Farsighted

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MicroscopeCalculationMagnificationEyepieceOpticsFocal LengthOptical DesignVision CareScience EducationOptical PhysicsMicroscopy Techniques