Quotient rule from product & chain rules | Derivative rules | AP Calculus AB | Khan Academy
TLDRThe video script explains the product rule and its application to derive the quotient rule in calculus. It emphasizes the product rule's two-term structure, where the derivative of one function is multiplied by the other, and vice versa. The script then demonstrates how to transform a quotient into a product form to apply the product rule with the chain rule, leading to the quotient rule's formula. The explanation highlights the mathematical relationship between the product and quotient rules, showing how the quotient rule results from subtracting the derivative of the numerator and the product of the numerator and the derivative of the denominator, all divided by the denominator squared.
Takeaways
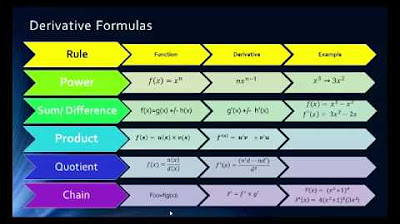
- 📚 The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
- 🔄 The quotient rule is derived from the product rule and is essentially a special case where one function is the reciprocal of the other.
- 🤔 Instead of memorizing the quotient rule separately, one can rederive it using the product rule and chain rule, which can be helpful for understanding and applying in problem-solving.
- 🌟 The key to applying the quotient rule is recognizing that a division can be rewritten as a product involving the reciprocal of the denominator function.
- 📈 The derivative of a function divided by another function involves taking the derivative of the numerator and applying the chain rule to the denominator.
- 🔢 The quotient rule can be expressed as (derivative of the numerator over the denominator) minus (the numerator times the derivative of the denominator), all over the square of the denominator.
- 🧩 The process of deriving the quotient rule from the product rule involves simplifying the expression by combining terms and manipulating fractions.
- 📊 When taking the derivative of a function in the denominator, there is a subtraction instead of addition as in the product rule.
- 🎯 The quotient rule is a powerful tool for solving calculus problems involving division of functions and can make calculations more efficient.
- 💡 Understanding the relationship between the product rule and the quotient rule can enhance problem-solving skills and provide a deeper understanding of calculus concepts.
- 🌐 The quotient rule is a fundamental concept in calculus that is often used in various mathematical and real-world applications.
Q & A
What is the product rule in calculus?
-The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
How can the product rule be applied to find the derivative of a quotient?
-By rewriting the quotient as the numerator function times the denominator function to the negative first power, the product rule can be applied with the chain rule to find the derivative of the quotient.
What is the quotient rule in calculus?
-The quotient rule is a formula derived from the product rule that allows for the efficient calculation of the derivative of a quotient of two functions.
How does the quotient rule relate to the product rule?
-The quotient rule is essentially a special case of the product rule where one of the functions is the reciprocal of the other, and it simplifies the process of finding the derivative of a quotient.
What is the chain rule in calculus?
-The chain rule is a method used to find the derivative of a composite function by differentiating the outer function with respect to the inner function, and then differentiating the inner function with respect to the variable.
How does the chain rule come into play when using the product rule to find the derivative of a quotient?
-The chain rule is used when differentiating the denominator function in the quotient, as it is considered an inner function with respect to the variable, and the derivative of the outer function (the reciprocal of the denominator function) is needed.
What is the final form of the derivative of a quotient of two functions according to the script?
-The final form of the derivative of a quotient of two functions is (f'(x)g(x) - f(x)g'(x)) / g(x)^2, where f'(x) is the derivative of the numerator function and g'(x) is the derivative of the denominator function.
Why might one choose to derive the quotient rule from the product rule rather than memorize it?
-Deriving the quotient rule from the product rule can provide a deeper understanding of the relationship between the two rules and reinforce the underlying principles of calculus, even though memorizing the quotient rule might be faster for some in certain situations.
What is the significance of the subtraction in the quotient rule formula?
-The subtraction in the quotient rule formula indicates that unlike the product rule, where the derivatives of the functions are added, in the quotient rule, the derivative of the numerator function times the derivative of the denominator function is subtracted from the product of the numerator function and the derivative of the denominator function.
What is the role of the denominator in the quotient rule formula?
-In the quotient rule formula, the denominator is squared and serves as the denominator of the entire fraction, ensuring that all terms are divided by the square of the denominator function.
How can the quotient rule be used to simplify calculus problems?
-The quotient rule can simplify the process of finding derivatives of complex functions, especially when dealing with quotients, by providing a direct formula that can be applied without needing to rederive the rule each time.
Outlines
📚 Product Rule and its Application to the Quotient Rule
This paragraph begins with a review of the product rule, which is essential for understanding the subsequent discussion on the quotient rule. The product rule states that the derivative of the product of two functions (f(x) and g(x)) is the derivative of the first function times the second function plus the first function times the derivative of the second function. The explanation is clear and provides a solid foundation for the application of the product rule to derive the quotient rule. The paragraph then transitions into discussing the quotient rule by transforming a division expression (f(x)/g(x)) into a form that allows the use of the product rule with a slight modification involving the chain rule. The detailed explanation leads to the derivation of the quotient rule, which is presented in a form that might differ from traditional calculus textbooks but is derived using fundamental rules. The paragraph emphasizes the convenience of understanding the relationship between the product and quotient rules, which can simplify problem-solving in calculus.
📉 Derivation and Simplification of the Quotient Rule
This paragraph delves deeper into the derivation of the quotient rule by applying the product rule and chain rule to the expression f(x)/g(x). It explains the process of transforming the division into a form that can be analyzed using the product rule and how the chain rule comes into play to account for the exponent in the denominator. The paragraph highlights the subtraction in the numerator, which is a key difference between the product and quotient rules, and the squaring of the second function in the denominator. The explanation is methodical, leading to a final expression of the quotient rule that matches the standard form taught in calculus courses. The paragraph concludes by reinforcing the idea that the quotient rule can be conveniently derived from the product rule and chain rule, offering an alternative perspective for solving calculus problems involving division of functions.
Mindmap
Keywords
💡Product Rule
💡Quotient Rule
💡Derivative
💡Chain Rule
💡Function
💡Calculus
💡Rate of Change
💡Slope
💡Composite Functions
💡Differentiation
💡Algebraic Manipulation
Highlights
The product rule states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
The quotient rule can be derived from the product rule and is essentially an application of the product rule with a negative exponent.
The key to understanding the quotient rule is to rewrite the division as a product involving a negative exponent, allowing the use of the product rule and chain rule.
When applying the quotient rule, the derivative of the numerator is multiplied by the denominator and the derivative of the denominator is multiplied by the numerator and then negated.
The quotient rule can be remembered as subtracting the product of the first function and the derivative of the second function from the product of the derivative of the first function and the second function, all divided by the square of the second function.
The quotient rule is sometimes easier to remember by comparing it to the product rule, noting the subtraction instead of addition in the formula.
The chain rule plays a crucial role in the application of the quotient rule, especially when dealing with the negative exponent in the denominator.
The process of deriving the quotient rule from the product rule involves recognizing the division as a product of the numerator and the reciprocal of the denominator.
The quotient rule is a fundamental concept in calculus that allows for the differentiation of more complex functions involving division.
The product rule is a foundational calculus concept that is essential for understanding the quotient rule and its application.
The quotient rule formula can be simplified by combining terms over a common denominator, which is the square of the denominator function.
The quotient rule provides a convenient shortcut for differentiating functions involving division, although it can be easily derived from the product rule.
Understanding the relationship between the product rule and the quotient rule can enhance problem-solving efficiency in calculus.
The quotient rule is often presented in calculus textbooks as a separate rule, but it can be derived from the product rule for a deeper understanding.
The process of deriving the quotient rule demonstrates the interconnectedness of fundamental calculus concepts and the power of logical reasoning in mathematics.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: