Logarithmic functions differentiation | Advanced derivatives | AP Calculus AB | Khan Academy
TLDRThe video script explains the process of finding the derivative of a composite function, Y, which is defined as the log base four of the expression X squared plus X. The explanation involves breaking down the problem into simpler functions, U(X) and V(X), calculating their derivatives, and then applying the chain rule to find the derivative of Y with respect to X. The final result is a detailed expression involving the natural log of four, X squared, and X, demonstrating the power rule and change of base formula in calculus.
Takeaways
- 📚 The problem involves finding the derivative of a composite function, Y = log base four of (X^2 + X).
- 🔍 The first step is to recognize that Y is a composite function and define an intermediate function U(X) = X^2 + X.
- 📈 To find the derivative of Y with respect to X, we also need to calculate the derivative of U with respect to X, which is U'(X) = 2X + 1 using the power rule.
- 🌟 The derivative of the log function, V(X), is given by V'(X) = 1 / (log base 4) * natural log of the argument, which in this case is X.
- 🔄 The chain rule is applied to find the derivative of Y, which states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function.
- 📝 V'(U(X)) is calculated by replacing X with U(X) in the expression for V'(X), leading to V'(U(X)) = (1 / (natural log of 4)) * U(X).
- 🧠 The final derivative of Y with respect to X is found by multiplying V'(U(X)) by U'(X), resulting in a new expression involving both V'(X) and U'(X).
- 📊 The expression simplifies to (2X + 1) / (natural log of 4) * (X^2 + X), which is the derivative of Y with respect to X.
- 🌐 Understanding the chain rule and how to apply it to composite functions is crucial for solving such calculus problems.
- 🎓 This script serves as a comprehensive guide for those learning about logarithmic functions, their derivatives, and the application of the chain rule in calculus.
Q & A
What is the given function Y in terms of X?
-The given function Y is defined as the logarithm base four of X squared plus X.
How is the function U(x) represented in the script?
-U(x) is represented as X squared plus X, which is the inner function before taking the logarithm.
What is the derivative U'(x) of the inner function U(x)?
-The derivative U'(x) is calculated using the power rule, which results in 2X + 1.
What is the role of the natural log in finding the derivative of Y with respect to X?
-The natural log is used to convert the logarithmic function into an exponential form, which simplifies the process of differentiation.
How is the derivative V'(x) of the logarithmic function expressed in the script?
-V'(x) is expressed as 1 over the natural log of the base four, which is equivalent to the derivative of the natural log function scaled by the base's natural log.
What is the chain rule used for in this context?
-The chain rule is used to find the derivative of the composite function Y with respect to X by differentiating the outer function V with respect to the inner function U(x), and then multiplying by the derivative of U(x).
How is V'(U(x)) calculated in the script?
-V'(U(x)) is calculated by replacing X in the expression for V'(x) with U(x), resulting in 1 over the natural log of four times U(x).
What is the final expression for the derivative of Y with respect to X?
-The final expression for the derivative of Y with respect to X is (2X + 1) over the natural log of four times (X squared plus X).
Why is it important to understand the chain rule in calculus?
-Understanding the chain rule is crucial as it allows us to differentiate complex composite functions, which is essential for solving problems in various fields such as physics, engineering, and economics.
What is the significance of the change of base formula in logarithmic differentiation?
-The change of base formula is significant as it allows us to convert logarithms with different bases into a form that is easier to differentiate, typically to the natural log, which simplifies the process.
How does the method of logarithmic differentiation help in solving complex functions?
-Logarithmic differentiation simplifies the process by transforming complex functions into logarithmic forms, which often makes the differentiation process more straightforward and manageable, especially when dealing with products or powers of variables.
Outlines
📚 Derivative of a Composite Function
This paragraph introduces the concept of finding the derivative of a composite function. It begins with a specific example where Y is defined as the logarithm base four of X squared plus X. The voiceover explains that this is a composite function and proceeds to break it down into two parts: U of X, which is X squared plus X, and the logarithmic function V, which is log base four of U of X. The paragraph then delves into calculating the derivatives of U and V with respect to X. The derivative of U with respect to X is found using the power rule, resulting in 2X + 1. For the derivative of V with respect to X, the voiceover uses the change of base formula to find that it is 1/(natural log of four) times X. Finally, the paragraph applies the chain rule to find the derivative of Y with respect to X. The chain rule states that the derivative of Y is the derivative of V with respect to U times the derivative of U with respect to X. The final expression for the derivative of Y with respect to X is given as (2X + 1) / (natural log of four) times (X squared + X).
Mindmap
Keywords
💡Derivative
💡Logarithm
💡Composite Function
💡Chain Rule
💡Power Rule
💡Natural Logarithm
💡Change of Base Formula
💡Exponent
💡Variable
💡Rate of Change
💡Function
Highlights
The derivative of Y with respect to X is discussed, involving a composite function.
The function Y is defined as the log base four of X squared plus X.
The concept of a composite function is introduced, where the log base four is not just of X, but of another expression involving X.
U of X is defined as X squared plus X, and its derivative U prime of X is calculated using the power rule.
The derivative of X with respect to X is given as one.
V of X is defined as the log base four of X, and its derivative V prime of X is discussed in relation to the natural log.
V prime of X is calculated using the change of base formula, involving the natural log of four.
The chain rule is introduced to find the derivative of Y with respect to X.
The derivative of V with respect to U, or V prime of U of X, is explained.
V prime of U of X is found by replacing X with U of X in the derivative of V.
The expression for the derivative of Y with respect to X is constructed using the natural log of four and U of X.
The derivative is expressed as a combination of U of X and U prime of X, with the natural log of four as a scaling factor.
The final form of the derivative of Y with respect to X is given as (2X + 1) times (X squared + X) over the natural log of four.
The process of finding the derivative involves a step-by-step application of the power rule, chain rule, and understanding of logarithms.
The explanation emphasizes the importance of recognizing the structure of composite functions and applying the appropriate rules for differentiation.
The use of the change of base formula for logarithms is highlighted as a key step in finding the derivative of V of X.
The transcript provides a clear and detailed walkthrough of the differentiation process, suitable for educational purposes.
Transcripts
Browse More Related Video

Exponential functions differentiation | Advanced derivatives | AP Calculus AB | Khan Academy

Chain rule with the power rule

Derivative of sin(ln(x_)) | Advanced derivatives | AP Calculus AB | Khan Academy

Product Rule With 4 Functions - Derivatives | Calculus
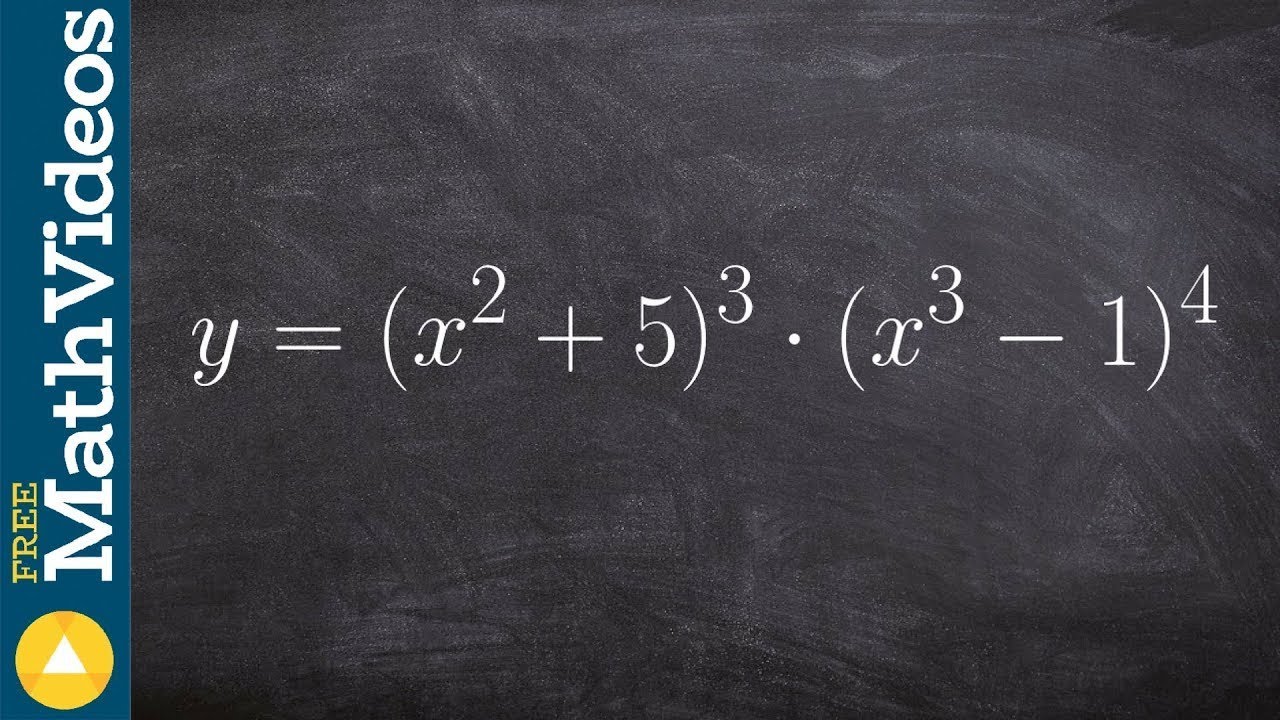
Taking the derivative of two binomials using product and chain rule

Worked example: Derivative of ln(ÃÂx) using the chain rule | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: