Static equilibrium (Examples)
TLDRIn this second tutorial of the static equilibrium series, the instructor guides students through solving a complex physics problem involving forces and tensions in a system with frictionless pulleys. The problem begins with identifying the section of the system where the most information is known, which is the part with weight W1. The weight is counteracted by the tension in the string, and since the pulleys are frictionless, the tension remains constant on both sides. The system is in equilibrium, meaning the vector sum of forces equals zero. The tutorial demonstrates how to resolve forces into components and apply trigonometric functions to find the unknown tensions (T1 and T2) and weights (W2 and W3). The process involves calculating the horizontal and vertical components of the forces, using sine and cosine functions for angles given in the problem. The instructor emphasizes the importance of considering the direction of forces when resolving vectors and provides a step-by-step approach to solving the problem. The video concludes with a teaser for the next tutorial, which will involve calculating torques and forces in a different scenario, encouraging students to attempt the problem before viewing the solution.
Takeaways
- 📐 **Identify the Section with Most Information**: Start by focusing on the part of the problem where you have the most information, which in this case is with weight W1.
- 🔍 **Understand the Pulley System**: Recognize that the pulleys are frictionless, which means the tension in the string (T1 and T2) remains the same on both sides of the pulley.
- ⚖️ **Sum of Forces in Equilibrium**: In a system at equilibrium, the vector sum of the forces equals zero. This is used to set up equations to solve for unknowns.
- 🎛️ **Resolve Forces into Components**: Break down forces into their horizontal (x) and vertical (y) components using trigonometric functions, considering the angles given.
- 🔢 **Consistent Sign Convention**: Choose a direction for positive and stick to it throughout the problem to avoid confusion in force calculations.
- 🔼 **Calculate Tensions (T1 and T2)**: Use the known weight W1 and the angles to calculate the tensions T1 and T2 in the system.
- 📉 **Determine Weight W2**: After finding T1 and T2, use the vertical forces and their components to find the weight W2 acting on the system.
- 📌 **Use the Junction Point**: Utilize the junction point to relate T2 to W3, as they are equal in a frictionless pulley system at equilibrium.
- 🔗 **Close the Loop**: Work from the most known information towards the unknowns, closing the loop by relating all the forces and tensions in the system.
- 🤔 **Consider Vector Directions**: Remember that the direction of vectors affects their signs in calculations, with leftward vectors often considered negative.
- 🧮 **Sum of Torques for Rotational Equilibrium**: When dealing with rotational equilibrium, ensure the sum of torques equals zero, indicating no rotation.
- 📚 **Educational Content**: The script is part of a tutorial series on static equilibrium, aiming to educate students on solving physics problems involving forces and equilibrium.
Q & A
What is the first step in solving a static equilibrium problem?
-The first step is to identify the section where you have the most information, which is typically where the forces and constraints are known.
What does it mean for a pulley to be frictionless in the context of this problem?
-A frictionless pulley implies that it does not change the tension in the rope or string passing through it. This means the tension on both sides of the pulley is the same.
How do you determine the direction of forces in a physics problem?
-You decide on a positive direction at the beginning of the problem and stick to it. Forces in the chosen positive direction are considered positive, and those in the opposite direction are negative.
Why do we set the sum of forces acting on a system in equilibrium to zero?
-A system is in equilibrium when the net force acting on it is zero. This means that the vector sum of all forces acting on the system in any direction must equal zero.
What is the relationship between the tensions T1 and T2 in the given problem?
-Since the pulleys are frictionless, the tension T1 on one side of the pulley is equal to the tension T2 on the other side.
How do you find the horizontal component of a force when given the angle it makes with the vertical?
-You can find the horizontal component of a force using the sine of the angle. The horizontal component (T1x or T2x) is equal to the force multiplied by the sine of the angle.
What is the significance of resolving forces into their components?
-Resolving forces into components allows us to break down forces into parts that act along specific axes (usually x and y axes). This is necessary to calculate the net force along each axis, which is crucial for equilibrium problems.
How do you find the vertical component of a force?
-The vertical component of a force is found using the cosine of the angle it makes with the horizontal. The vertical component (T1y or T2y) is equal to the force multiplied by the cosine of the angle.
What is the process of closing the loop in a static equilibrium problem?
-Closing the loop involves moving from the part of the system where you have the most information to the part where you have the least, using the known forces and constraints to find the unknowns step by step.
Why is it important to consider both the horizontal and vertical components of forces in equilibrium problems?
-Considering both components is important because a system is in equilibrium only when the net force in both the horizontal and vertical directions is zero. This ensures that there is no net force or torque causing motion.
How do you find the weight (W2) in the system using the horizontal and vertical components of the tensions?
-After finding T1 and T2, you can use the vertical components of these tensions along with the known weight W1 to establish an equation for W2. By summing the vertical forces to zero, you can solve for W2.
What is the final step after finding W2 in the system?
-The final step is to find the third weight (W3) using the known values of T2 and the fact that the system is in equilibrium. Since T2 is equal to W3, you can directly determine W3 from the calculated T2.
Outlines
📚 Introduction to Static Equilibrium Problem Solving
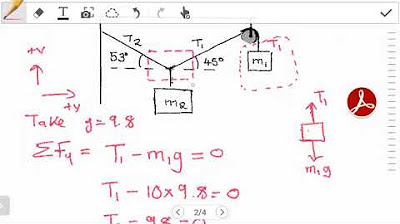
The paragraph introduces the second tutorial in a series on static equilibrium. The speaker recaps a question from the previous video and encourages students to have attempted it. The focus is on identifying the most informative section of the problem, which in this case involves knowing the weight 'w1'. The explanation then delves into the forces acting on the system, highlighting the downward weight 'w1' and the upward tension 't1' in a frictionless pulley system. The concept of vector sum of forces equaling zero in an equilibrium state is emphasized, leading to the calculation of 't1' being equal to 800 newtons, given 'w1' is 800 newtons.
📐 Resolving Forces and Free Body Diagrams
This paragraph discusses the process of drawing a free body diagram to understand the forces acting through a specific point in the system. The speaker identifies horizontal and vertical forces, including 't1', 't2', and 'w2', and notes the importance of considering angles given between the vector and the vertical. The paragraph explains how to resolve these forces into components using trigonometric functions, specifically sine and cosine, to find the horizontal components of 't1' and 't2'. The vector sum of forces in the x-direction is set to zero, leading to the calculation of 't2' as 671.3 newtons.
🔍 Vertical Force Analysis and Calculation of w2
The speaker continues with the vertical force analysis at a junction point. The forces considered are the vertical components of 't1' and 't2', as well as the weight 'w2'. Using trigonometric relationships within a rectangle formed by the forces, the speaker demonstrates how to calculate the vertical components 't1y' and 't2y'. The sum of these forces, along with 'w2', should equal zero in the y-direction for the system to be in equilibrium. By substituting known values, the weight 'w2' is found to be 1044 newtons.
🔗 Finding the Relationship Between t2 and w3
The paragraph focuses on the relationship between the tension 't2' and the weight 'w3'. Given that 't2' has been previously determined and the pulley system is massless and frictionless, the speaker explains that 't2' is equal to 'w3'. By this relationship, 'w3' is calculated to be 671.3 newtons, following the principle that in equilibrium, the net force must be zero.
🎓 Conclusion and Preview of the Next Problem
The speaker concludes the current problem and previews the next question, which involves calculating the sum of torques in a system in equilibrium. The hint provided suggests starting with the calculation of torques and then finding the forces that result in a net torque of zero. The speaker encourages students to attempt the problem, offers help for those struggling with vector resolution, and invites engagement through comments.
Mindmap
Keywords
💡Static Equilibrium
💡Tension in a String
💡Frictionless Pulleys
💡Vector Sum
💡Free Body Diagram
💡Component Forces
💡Trigonometry
💡Weight (W1, W2, W3)
💡Newton's Laws of Motion
💡Equation of Equilibrium
💡Torques
Highlights
Introduction to the second tutorial in the static equilibrium series.
Emphasis on identifying the section of the problem with the most known information.
Explanation of how to deal with frictionless pulleys and their effect on tension.
Demonstration of isolating a section of the system to analyze forces acting on it.
Use of positive and negative directions in physics to define forces.
Equilibrium condition: the sum of forces (vector sum) equals zero.
Calculation of tension T1 using the weight W1 and equilibrium condition.
Closing the loop at a junction to analyze forces through a point.
Resolution of forces into components using trigonometric functions.
Use of sine and cosine to find the horizontal and vertical components of forces.
Determination of T2 through the horizontal force equilibrium.
Calculation of W2 using the vertical force equilibrium and resolved components.
Finding W3 by relating T2 to W3 at the pulley, considering the system's equilibrium.
Simple concept of equilibrium applied to find W3 equals T2.
Invitation for students to try solving the problem before viewing hints.
Strategy for solving the next problem using the sum of torques and force equilibrium.
Offer to upload a video explaining how to resolve vectors for those who struggle with the concept.
Encouragement for students to engage with the material and apply the concepts to solve problems.
Transcripts
Browse More Related Video
Introduction to Static Equilibrium
Physics 15 Torque Example 2 (2 of 7) Mass on Rod and Cable
Newton's Second Law Exam Question: Two-body systems Pulley practice

Physics 15 Torque Example 4 (4 of 7) The Diving Board
Physics 15 Torque Example 3 (3 of 7) Mass on Rod and Cable

Force Vectors Along a Line | Mechanics Statics | (Learn to solve any question)
5.0 / 5 (0 votes)
Thanks for rating: