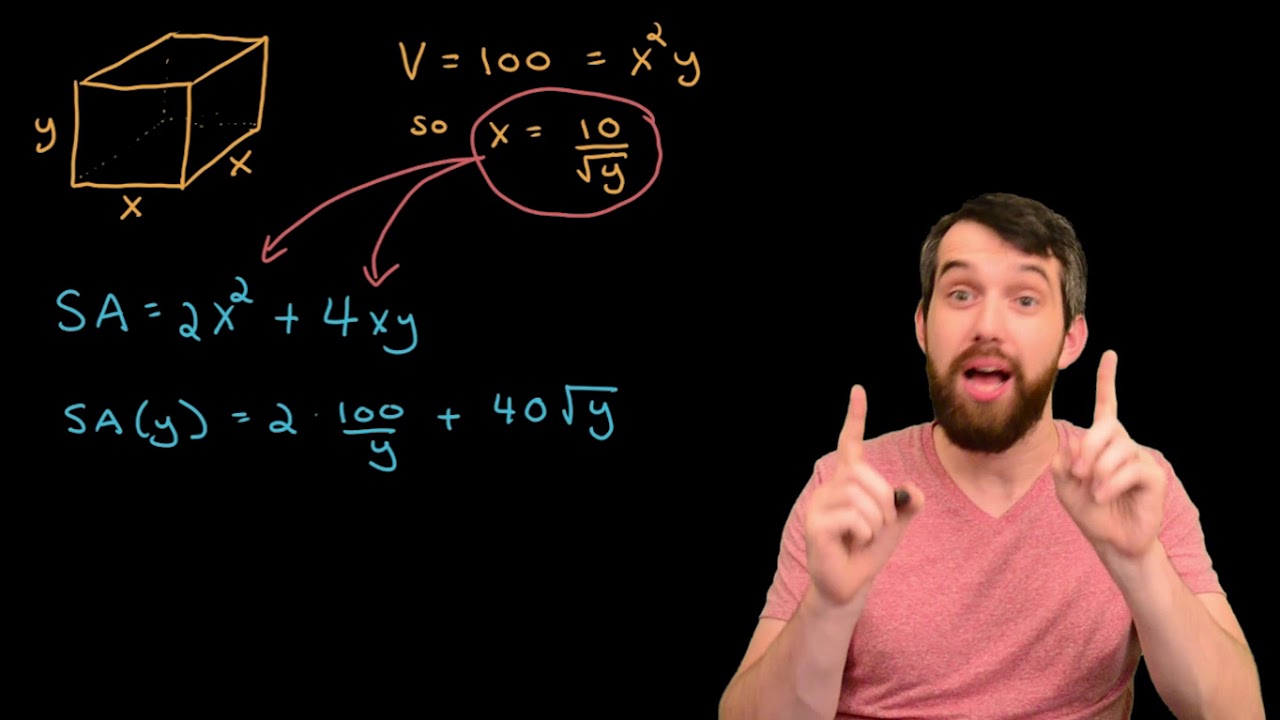Ex: Optimizing the Volume of a Box With Fixed Surface Area
TLDRThe video script discusses the application of calculus in real-life optimization problems, particularly focusing on maximizing or minimizing variables such as cost, energy, or heat in a system. It presents a specific example of optimizing the volume of an open-top box with a square base, given a constraint on the available material. The presenter outlines a step-by-step approach, starting with drawing a diagram to visualize the problem, then formulating equations based on the constraints and the volume to be optimized. The process involves differentiating the volume equation with respect to one variable, using the constraint to eliminate the other variable, and finding critical points by setting the derivative to zero. The script emphasizes the importance of understanding whether these critical points represent maxima or minima, using the first derivative test and considering the endpoints. Finally, it demonstrates how to calculate the dimensions that yield the maximum volume, emphasizing the need to answer the exact question posed by the problem.
Takeaways
- 📐 **Optimization in Real Life**: Real-world problems often involve optimizing for various factors like maximizing profit or minimizing costs.
- 🧮 **Importance of Calculus**: Calculus and STEM disciplines are crucial for solving optimization problems which are prevalent in everyday scenarios.
- 📈 **Drawing a Picture**: The first step in most optimization problems is to visualize the scenario, label variables, and understand the situation clearly.
- 📏 **Defining Variables**: Assign variables to the different dimensions of the problem, such as length (L) and height (H) in the case of the box.
- 📉 **Constraints and Optimization Equations**: Write down equations that represent the constraints of the problem and what you aim to optimize.
- 📦 **Volume as the Optimization Goal**: In the given example, the goal is to maximize the volume of a box with a square base and no top.
- 🔢 **Solving for a Single Variable**: Use the constraint equation to express the optimization equation in terms of a single variable to simplify the problem.
- 🤔 **Derivatives and Critical Points**: Take the derivative of the volume function with respect to one variable and set it to zero to find critical points.
- 📌 **Physical Plausibility**: Consider whether the critical points make physical sense in the context of the problem, discarding negative or zero values where applicable.
- 🔍 **First Derivative Test**: Use the first derivative test to determine if a critical point is a maximum, minimum, or neither by analyzing the sign of the derivative.
- 📐 **Final Dimensions**: After finding the optimal value for one variable, use the constraint equation to find the corresponding value for the other variable.
- 📝 **Answering the Question**: Ensure that the final answer addresses the specific question asked, whether it's for dimensions, volume, or another aspect of the optimization problem.
Q & A
What is the main concept discussed in the transcript?
-The transcript discusses the concept of optimization in real-life applications, focusing on both maximization and minimization problems, and how calculus and STEM disciplines are essential in solving these problems.
Why is it necessary to draw a picture when dealing with optimization problems?
-Drawing a picture helps to visualize the problem, label the variables clearly, and understand the relationships between different components of the problem, which is crucial for formulating and solving the equations involved.
What is the first step in solving an optimization problem?
-The first step in solving an optimization problem is to draw a diagram that represents the situation, label all the variables, and establish a clear understanding of what is happening in the problem.
What is the constraint in the given box optimization problem?
-The constraint in the box optimization problem is that there is only 12,000 square centimeters of material available to create the box, which affects the dimensions of the base and the sides.
How is the volume of the box calculated in the script?
-The volume of the box is calculated by considering the area of the square base (L^2) and multiplying it by the height (H), resulting in the formula V = L^2 * H for the volume.
What is the purpose of the constraining equation in the optimization problem?
-The constraining equation is used to express the limitations or restrictions of the problem, such as the amount of material available. It helps in setting up the conditions that the solution must satisfy.
How does the script solve for the height (H) of the box using the constraint?
-The script solves for the height (H) by rearranging the constraint equation to isolate H, resulting in the formula H = (12,000 - L^2) / (4L).
What mathematical technique is used to find the dimensions that maximize the volume of the box?
-The script uses calculus, specifically taking the derivative of the volume function with respect to one variable (after eliminating the other using the constraint) and setting it to zero to find critical points that could potentially maximize the volume.
How does the first derivative test help in determining whether a critical point is a maximum or minimum?
-The first derivative test examines the sign of the derivative before and after the critical point. If the derivative changes from positive to negative, it indicates a maximum; if it changes from negative to positive, it indicates a minimum.
What is the final calculated dimension for the length (L) that maximizes the volume of the box?
-The final calculated dimension for the length (L) that maximizes the volume of the box is 20√10 centimeters.
How does the script ensure that the critical number found indeed corresponds to a maximum volume?
-The script ensures this by checking the endpoints of the domain (which do not make physical sense for a box) and using the first derivative test to confirm that the critical number corresponds to a maximum by observing the change in the derivative's sign around the critical point.
Outlines
📏 Introduction to Optimization in Calculus
This paragraph introduces the concept of optimization in real-life scenarios, where the goal is to maximize or minimize certain variables such as money, cost of materials, energy, or heat. It emphasizes the importance of calculus and STEM disciplines in solving these optimization problems. The speaker outlines the process of tackling an optimization problem by first drawing a diagram to visualize the variables and constraints. A specific example of a square-bottomed box is used to illustrate the steps, starting with defining variables for length (L) and height (H), and setting up equations based on the given constraints and what is to be optimized—in this case, the volume of the box.
🧮 Setting Up the Optimization Equations
The speaker continues by formulating the constraint equation for the box-making problem, which is based on the limitation of 12,000 cm² of material. This leads to an equation involving L (the length of the square base) and H (the height of the box). The next step is to express the volume of the box as an optimizing equation, which is a function of L and H. To solve for optimization, the goal is to manipulate these equations to express the volume in terms of a single variable. This is achieved by substituting the expression for H from the constraint equation into the volume equation, resulting in a simplified equation in terms of L only, which can then be differentiated to find the critical points for optimization.
🔍 Deriving the Solution and Analyzing the Results
After simplifying the volume equation to a function of L only, the speaker proceeds to take the derivative of this function and sets it to zero to find critical points. The resulting equation is solved to find the value of L that corresponds to a potential maximum or minimum. Considering the physical constraints of the problem, the negative solution is discarded, and the positive value of L is identified as the critical point where the maximum volume occurs. The speaker then uses the constraint equation to find the corresponding value of H. Finally, the speaker summarizes the key steps in solving optimization problems: diagramming, standardizing variables, writing equations, differentiating, classifying critical numbers, and answering the specific question asked by the problem.
Mindmap
Keywords
💡Optimization
💡Calculus
💡Square Bottom Box
💡Constraint
💡Volume
💡Derivative
💡Critical Number
💡First Derivative Test
💡Physical Interpretation
💡Maximization Problem
💡Minimization Problem
Highlights
The importance of optimization in real-life applications, such as maximizing money in a bank account or minimizing costs and energy.
The necessity of learning calculus and STEM disciplines due to the widespread need for optimization.
The approach to solving optimization problems by using tools developed in calculus.
The illustration of an optimization problem involving a square-bottom box with a specific material constraint.
The first step in optimization problems is to visualize the scenario by drawing a diagram and labeling variables.
The mathematical representation of the box using variables L for length and H for height.
The formulating of a constraining equation based on the available material for the box construction.
Deriving the optimizing equation for the volume of the box, aiming to maximize this quantity.
The substitution of the constraining equation into the optimizing equation to eliminate one variable.
Differentiating the volume function with respect to the single remaining variable to find critical points.
Using the first derivative test to determine whether a critical point is a maximum or minimum.
Considering physical constraints, such as non-negative dimensions, to validate the mathematical solution.
The calculation of the critical value for L that maximizes the volume of the box.
The determination of the corresponding height H using the relationship derived from the constraints.
The conclusion that the maximum volume occurs when the height is half the length of the base.
The common steps in solving optimization problems, including diagramming, standardizing variables, writing equations, differentiating, classifying critical numbers, and answering the question.
The emphasis on carefully reading the problem to answer the exact question asked, which may vary in different problem contexts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: