Ch. 13.3 Tangent Lines and Derivatives
TLDRThis lecture delves into the fundamental concepts of calculus, focusing on tangent lines and derivatives as the core of calculus one. It explains the average rate of change and transitions to the instantaneous rate of change, which is the derivative. The instructor illustrates the process of finding the derivative through the difference quotient and applies it to a function to demonstrate the calculation of the slope of the tangent line at a specific point. The lecture concludes with examples that show how to determine the equation of the tangent line using the slope and a point on the curve.
Takeaways
- 📚 The lesson is focused on the concept of tangent lines and derivatives, which are central to calculus and revisited in more advanced courses.
- 🔍 The average rate of change of a function is the difference in outputs over the difference in inputs, which is constant for a straight line but varies for curves.
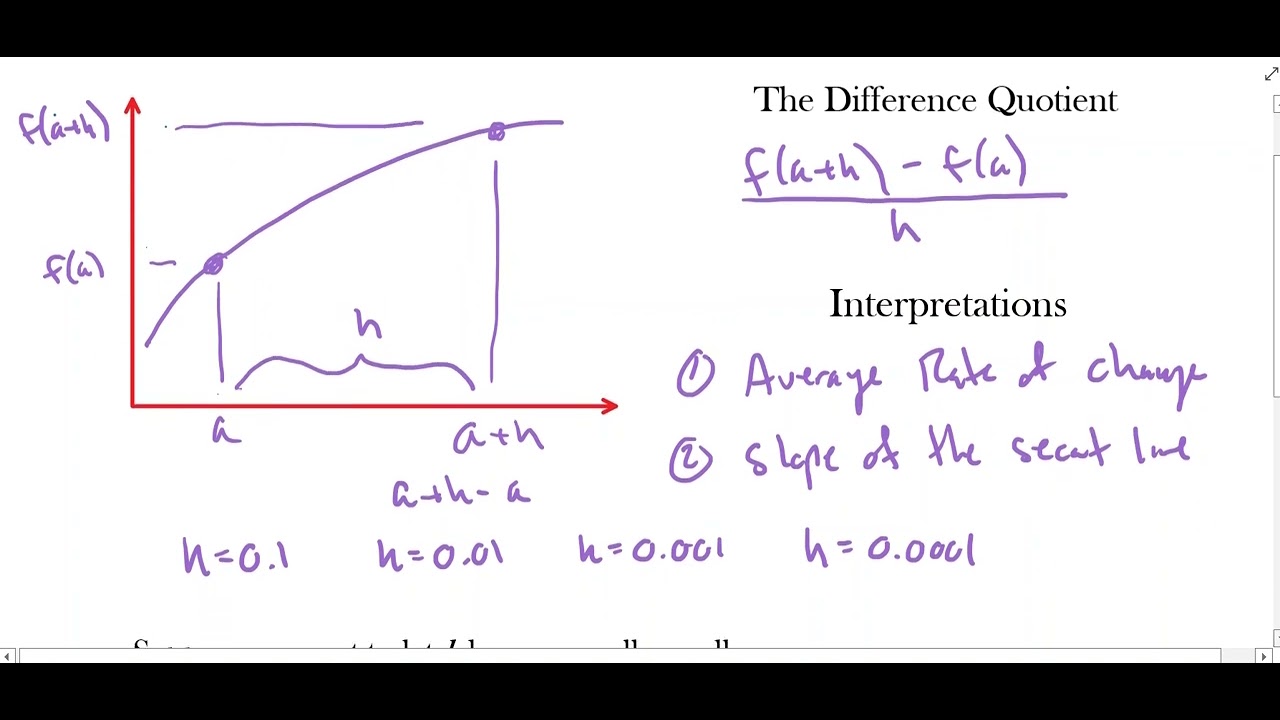
- 📈 The slope of a line connecting two points on a curve represents the average rate of change between those points, which can be found using the difference quotient formula.
- 🔺 The difference quotient is a mathematical expression that helps in understanding the relationship between the change in the function's output and the change in input.
- 📉 As 'h' approaches zero, the secant line through points 'a' and 'a+h' becomes a tangent line, representing the instantaneous rate of change at point 'a'.
- 🔑 The derivative of a function at a point is the limit of the difference quotient as 'h' approaches zero, indicating the slope of the tangent line at that point.
- 📝 The derivative is denoted as 'f' prime of 'a' and represents the instantaneous rate of change of the function at a specific point, which is a fundamental concept in calculus.
- 🚗 An example given is driving on an on-ramp, where the speed (rate of change) is not constant, illustrating the concept of instantaneous rate of change.
- 📉 The process of finding the derivative involves algebraic simplification to make the expression continuous at 'h' equals zero, which gives the slope of the tangent line.
- 📝 The equation of the tangent line can be found using the slope of the tangent (the derivative) and a point on the curve, typically the point of interest where the derivative is evaluated.
- 📈 The script provides step-by-step examples of finding the derivative and the equation of the tangent line for a given function, emphasizing the practical application of these concepts.
Q & A
What is the main topic of the last section of Chapter 13 in the course?
-The main topic is tangent lines and derivatives, which is a fundamental concept in calculus.
Why is the concept of tangent lines and derivatives considered important in calculus?
-Tangent lines and derivatives are important because they are revisited in higher-level calculus courses and are the central theme around which calculus one revolves.
What is the average rate of change of a function from one input to another?
-The average rate of change of a function is the difference in their outputs divided by the difference in the inputs.
How is the average rate of change related to the slope of a line?
-For a straight line, the average rate of change is a constant value, which is the slope of the line.
What is the difference quotient and how does it relate to calculus?
-The difference quotient is an expression that calculates the average rate of change of a function as the distance between two points (h) approaches zero, which is foundational in understanding derivatives in calculus.
What is a secant line and how does it differ from a tangent line?
-A secant line is a line that passes through a curve and connects two points on the curve. A tangent line, on the other hand, intersects the curve at only one point.
What happens to the secant line as the distance 'h' between two points on the curve approaches zero?
-As 'h' approaches zero, the secant line becomes the tangent line, representing the instantaneous rate of change at a specific point on the curve.
What is the derivative of a function at a point and how is it represented?
-The derivative of a function at a point is the limit of the difference quotient as 'h' approaches zero, representing the instantaneous rate of change at that point. It is represented as f'(a) or dy/dx.
How can you find the equation of the tangent line to a curve at a specific point?
-To find the equation of the tangent line, you need the slope of the tangent line (the derivative at that point) and a point on the curve that the tangent line touches.
What is the significance of the instantaneous rate of change in understanding the behavior of a function at a specific point?
-The instantaneous rate of change, derived from the derivative, provides insight into how the function is changing at that exact moment, which is crucial for understanding phenomena like speed changes in motion.
Can you provide an example of how to find the derivative of a function given in the script?
-Yes, for the function f(x) = 2/(x+2), to find the derivative at x=3, you would calculate the limit of the difference quotient as h approaches zero, which simplifies to -2/25, indicating the function is decreasing at that point.
Outlines
📚 Introduction to Tangent Lines and Derivatives
This paragraph introduces the topic of tangent lines and derivatives, emphasizing their importance in calculus. It explains the concept of the average rate of change for both straight lines and curves, using the difference in outputs over the difference in inputs. The paragraph also introduces the difference quotient, which is a key concept in understanding how calculus revolves around the study of tangent lines and derivatives. The instructor hints at the possibility of covering additional sections in the future but focuses on the foundational aspects of calculus for now.
📉 Transition from Average to Instantaneous Rate of Change
The instructor discusses the transition from considering the average rate of change to the instantaneous rate of change, which is the focus of derivatives in calculus. By examining the behavior of a secant line as the distance 'h' between two points on a curve approaches zero, the slope of the secant line becomes the slope of the tangent line at a single point. This is the instantaneous rate of change, and the limit process used to find this slope is defined as the derivative of the function at that point. The paragraph uses the analogy of driving on an on-ramp to illustrate the concept of changing rates over time, highlighting the relevance of the instantaneous rate of change in real-world scenarios.
🔍 Calculating the Derivative and Tangent Line Example
This paragraph provides a step-by-step example of how to calculate the derivative of a function to find the instantaneous rate of change at a specific point. Using the function f(x) = 2 / (x + 2), the instructor demonstrates the process of taking the limit as h approaches zero and algebraically simplifying the expression to find the derivative at x = 3. The result is a negative slope, indicating the function is decreasing at that point. The instructor then explains how to use this derivative to find the equation of the tangent line at x = 3, using the point-slope form of a line and the shared point on the curve and the tangent line.
📈 Deriving the Equation of a Tangent Line Given a Derivative
The final paragraph extends the concept of finding the equation of a tangent line when the derivative is known. The instructor provides an example where the derivative at x = 5 is given as 2, and the function value at this point is 10. Using this information, along with the slope-intercept form of a line, the instructor derives the equation of the tangent line. The paragraph also discusses how to find the outputs for additional points on the tangent line by using the derived equation, showcasing the practical application of derivatives in determining the behavior of a function at specific points.
Mindmap
Keywords
💡Tangent Lines
💡Derivatives
💡Average Rate of Change
💡Difference Quotient
💡Instantaneous Rate of Change
💡Secant Line
💡Limit
💡Slope
💡Function
💡Continuous
💡Algebraic Methods
Highlights
Introduction to the importance of tangent lines and derivatives in calculus.
Explanation of the average rate of change of a function from one input to another.
Clarification that the average rate of change is constant for a straight line but varies for a curve.
Introduction of the difference quotient and its relation to the average rate of change.
Re-framing the difference quotient to focus on the variable 'h' instead of two fixed points.
Definition and explanation of a secant line as a line passing through two points on a curve.
Discussion on the concept of the slope of a secant line representing the average rate of change.
Transition from secant line to tangent line as the distance 'h' approaches zero.
Differentiation between the average rate of change and the instantaneous rate of change.
Illustration of the concept of instantaneous rate of change with the example of driving on an on-ramp.
Introduction to the derivative of a function at a point and its notation.
Derivation of the derivative for the function 2/(x+2) at x=3 through algebraic simplification.
Explanation of the significance of the negative slope in the derivative indicating a decreasing function.
Process of finding the equation of the tangent line given the slope and a point on the curve.
Graphical representation of the function, the tangent line, and the point of tangency.
Application of the concept of the tangent line and derivative to find the equation of a tangent line at x=5 with a given slope.
Final example demonstrating the calculation of points on the tangent line using the slope and a known point.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: