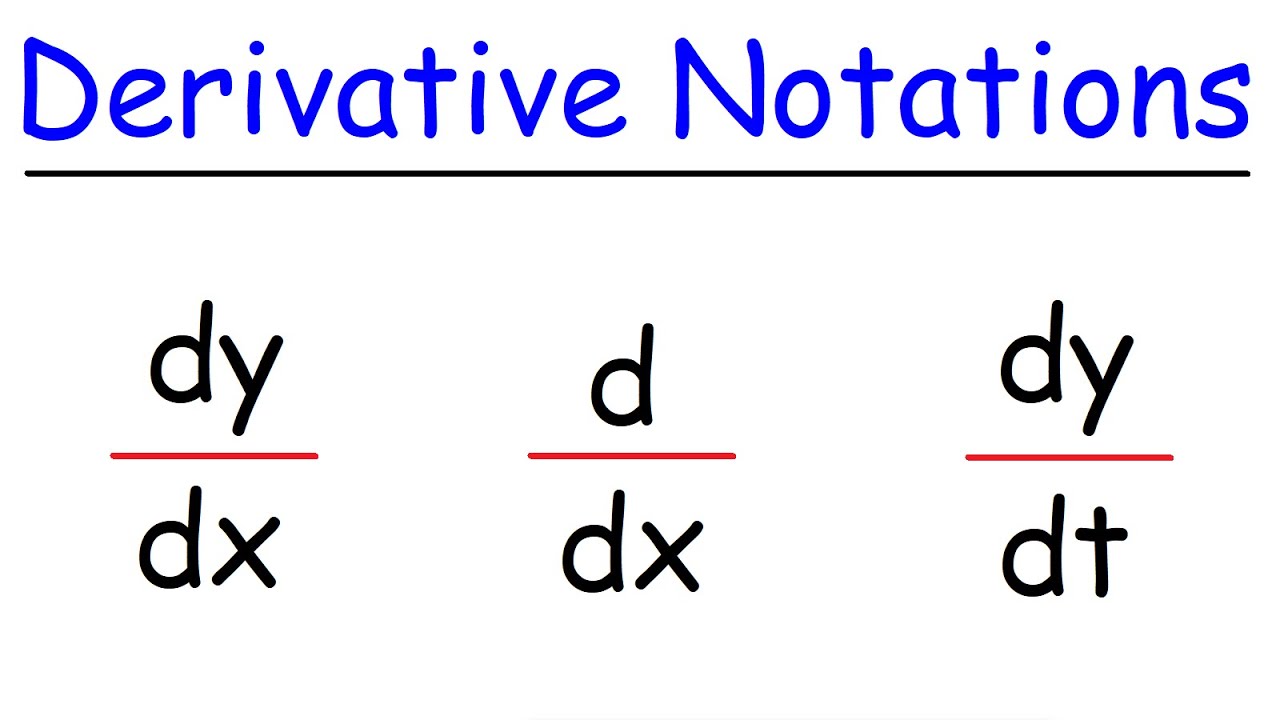
find x' for the function x(t) defined implicitly. derivative of implicit function class 12

mathmontrealmath
11 Mar 202208:41
EducationalLearning
32 Likes 10 Comments

TLDRThe video script appears to be a tutorial on calculus, specifically focusing on the concept of derivatives in a different context than the standard x and y variables. The speaker emphasizes the importance of understanding that when a function is defined in terms of another variable, such as x(t), the derivative with respect to that variable, in this case t, is crucial. The discussion delves into the nuances of derivatives, including the derivative of constants, the product rule, and the need to adapt to new concepts. The speaker uses the example of a function x(t) to illustrate the process of finding derivatives, stressing that the derivative of x with respect to t should be denoted as x'(t). The tutorial aims to clarify the concept of derivatives in a broader mathematical context and encourages learners to grasp the underlying principles rather than just memorizing formulas.

Takeaways
  • 📚 The script discusses the concept of derivatives in calculus, emphasizing the importance of understanding the context in which a derivative is taken.
  • 🔑 When taking the derivative of a function defined with respect to 't', 'x' behaves like the dependent variable 'y' in the standard form of differentiation.
  • 📐 The derivative of 't' with respect to 't' is 1, which is a fundamental concept in calculus that is highlighted in the script.
  • 🧮 The derivative of a constant is zero, which is a basic rule of differentiation, and the script reinforces this by discussing the derivative of 't' in different contexts.
  • 🔍 The script clarifies that the derivative of '3x' with respect to 't' is not simply '3', but '3x' prime, indicating the need to consider the function's dependency on 't'.
  • 🤔 The concept of 'x' as a function of 't' is a shift from the standard form, and the script encourages adapting to this new perspective for accurate differentiation.
  • 📉 The script touches on the product rule in differentiation, which applies when differentiating a product of two functions.
  • 🔄 It is emphasized that when differentiating with respect to 't', the notation 'x prime' should be used to denote the derivative of 'x' with respect to 't'.
  • 📝 The script provides a step-by-step approach to differentiating a function of 't', including the application of the product rule and understanding the role of each variable.
  • 🌐 The importance of being flexible with variable names and understanding the underlying mathematical principles across different notations and contexts is stressed.
  • 🎓 The script encourages learning and adapting to new concepts, which is crucial for a deeper understanding of calculus and differentiation.
Q & A

  • What is the context of the derivative being discussed in the transcript?

    -The context is a mathematical discussion where 't' is treated as a variable similar to 'x' in standard calculus problems, and 'x' is considered a function of 't'. The derivative in this context is taken with respect to 't', not 'x'.

  • What is the derivative of 't' in the given context?

    -In the context provided, the derivative of 't' with respect to itself is 1, as 't' is behaving like the independent variable in a standard calculus problem.

  • What does 'x prime' represent in the transcript?

    -'X prime' represents the derivative of 'x' with respect to 't'. It is used to denote the rate of change of 'x' as 't' changes, which is a key concept when 'x' is a function of 't'.

  • Why does the speaker emphasize that 'x' behaves like 'y' in this context?

    -The speaker emphasizes this to clarify that although the symbols used are different ('x' as a function of 't'), the mathematical operations and rules, such as differentiation, apply in the same way as they would if 'y' were a function of 'x'.

  • What is the standard form of differentiation that the speaker refers to?

    -The standard form the speaker refers to is d/dx(y) = y', where 'y' is a function of 'x', and 'y'' (y prime) represents the derivative of 'y' with respect to 'x'.

  • How does the speaker use the product rule in the context of the problem?

    -The speaker applies the product rule in the context of a function that is a product of two other functions, 'u' and 'v', where the derivative is u'v + uv'. This is a standard rule in calculus for differentiating products of functions.

  • What is the significance of treating 't' as a constant when differentiating?

    -Treating 't' as a constant is significant because it allows the differentiation to proceed as if 't' does not change. This is useful when 't' is not the variable with respect to which the derivative is being taken, such as when 'x' is a function of 't'.

  • Why does the derivative of a constant with respect to 't' result in zero?

    -The derivative of a constant with respect to any variable, including 't', is zero because a constant does not change as the variable changes, hence there is no rate of change.

  • What does the speaker mean by 'the one that is given' when discussing the derivative?

    -The speaker is referring to the constant term in the expression that is being differentiated. When differentiating a constant term with respect to a variable, the derivative is zero, as constants do not change with the variable.

  • What is the role of the chain rule in the context of the problem discussed?

    -The chain rule is implied when the speaker discusses the derivative of a function of 't', which is 'x'. The chain rule is used to find the derivative of a composite function, in this case, the function 'x' as a function of 't'.

  • How does the speaker use the term 'lon x' in the transcript?

    -The term 'lon x' seems to be a mispronunciation or typo for 'ln x', which represents the natural logarithm of 'x'. The speaker discusses the derivative of 'ln x' with respect to 't', which involves the chain rule.

  • What is the final step the speaker instructs to do after the differentiation process?

    -The final step the speaker instructs is to plug in the values for 't' and 'x' into the derived expression. In this case, 't' is zero and 'x' is one, which would finalize the calculation of the derivative at that specific point.

Outlines
00:00
🧮 Understanding Derivatives in a New Context

The first paragraph delves into the concept of derivatives in calculus, focusing on the differentiation of functions with respect to a variable 't' instead of the standard 'x'. It emphasizes the need to adapt to new contexts where 'x' is treated as a function of 't', and thus 'x' behaves like 'y' in traditional calculus. The speaker clarifies the confusion between the derivative of 't' and 'x' in this new context, explaining that the derivative of a constant is zero and that the derivative of '3t' would simply be '3', not '3t'. The paragraph also touches on the standard form of derivatives and the importance of recognizing 'x' as a dependent variable in this scenario.

05:00
📚 Applying Product Rules and Derivatives

The second paragraph continues the discussion on derivatives, introducing the concept of product rules in the context of 'x' as a function of 't'. It stresses the importance of recognizing the derivative of 'x' (denoted as 'x prime') when differentiating expressions involving 'x'. The speaker provides a step-by-step approach to differentiating composite functions, such as 'e^(t)' and 'x^(t)', and explains the role of the product rule in these cases. The paragraph concludes with an example calculation, reinforcing the idea that the derivative of 'x' with respect to 't' should be represented as 'x prime', and highlights the need to be comfortable with different letter names for variables across various mathematical contexts.

Mindmap
Keywords
💡Derivative
The derivative is a fundamental concept in calculus that represents the rate at which a function changes with respect to its variable. In the video, the concept is explored in the context of functions defined by 't', where the derivative of 't' with respect to 't' is discussed, and it is shown to be 1, illustrating the rate of change.
💡Function of t
This term refers to a mathematical function where 't' is the independent variable. The video emphasizes that when 'x' is expressed as a function of 't', it behaves similarly to 'y' in the standard form of calculus, and thus its derivative with respect to 't' is denoted as 'x prime'.
💡Product Rule
The product rule is a formula used in calculus to find the derivative of a product of two functions. In the video, the product rule is mentioned in the context of differentiating a function involving 'u' and 'v', where the derivative of the product is the derivative of the first function times the second function plus the first function times the derivative of the second.
💡Rate of Change
The rate of change is a measure of how much a quantity changes with respect to another quantity. In the video, it is discussed in the context of the derivative of 't' and 'x', highlighting how it is calculated differently based on whether 'x' is a function of 't' or a constant.
💡Standard Form
The standard form in calculus typically refers to the notation dy/dx for derivatives, where 'y' is a function of 'x'. The video script discusses the concept of changing the standard form to accommodate functions of 't', emphasizing the need to adapt to new contexts and notations.
💡Context
Context is the setting in which events or ideas occur and which provides them with their specific meaning. In the video, the importance of understanding the context of mathematical expressions is stressed, particularly when dealing with derivatives and the behavior of variables like 'x' and 't'.
💡u prime and v prime
In the video, 'u prime' and 'v prime' are used to denote the derivatives of functions 'u' and 'v', respectively. This notation is part of the explanation of how to apply the product rule when differentiating a function of 't'.
💡Constant
A constant is a value that does not change. In the context of the video, the derivative of a constant is discussed, and it is correctly stated that the derivative of a constant with respect to any variable is zero.
💡Natural Exponential Function
The natural exponential function, often denoted as 'e^t', is a mathematical function involving the mathematical constant 'e'. In the video, it is mentioned in the context of differentiating exponential functions with respect to 't'.
💡Differentiation
Differentiation is the process of finding the derivative of a function. The video script delves into the process of differentiation, particularly when the function involves variables 'x' and 't', and how the process changes based on the function's context.
💡Independent Variable
An independent variable is a variable that can be changed or varied independently of other variables. In the video, 't' is discussed as an independent variable in the context of functions defined by 't', and how its derivative affects the overall function.
Highlights

The rate of change of t is zero

Derivative of x with respect to t is x prime

Derivative of a constant is zero

Derivative of t with respect to t is one

x behaves like y in this context

t behaves like x in this context

Different letter names can be used for variables

Applying the product rule to u prime v plus v prime u

Derivative of ln(x) is 1/x

Derivative of e^t is e^t

Derivative of a function of t with respect to t is the rate of change with respect to t

Adapting to new concepts is important for learning

In the standard form, dy/dx = f'(x) represents the derivative of y with respect to x

When changing variable names, x behaves like y and t behaves like x

Applying the product rule to x(t) and t(x) requires treating t as the independent variable

The derivative of x with respect to t should be denoted as x prime

In this context, the derivative of 3t is simply 3

The derivative of t with respect to t is 1, not zero

The derivative of x with respect to t is x prime, not just 1

Transcripts

Browse More Related Video

Multivariable chain rule

dy/dx, d/dx, and dy/dt - Derivative Notations in Calculus

The Multi-Variable Chain Rule: Derivatives of Compositions

Partial Derivatives

Derivatives of Integrals (w/ Chain Rule)

Partial Derivatives - Multivariable Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusDerivativesEducationalMusicalMathematicsFunctionProduct RuleDifferentiationLearningConceptsMath Education