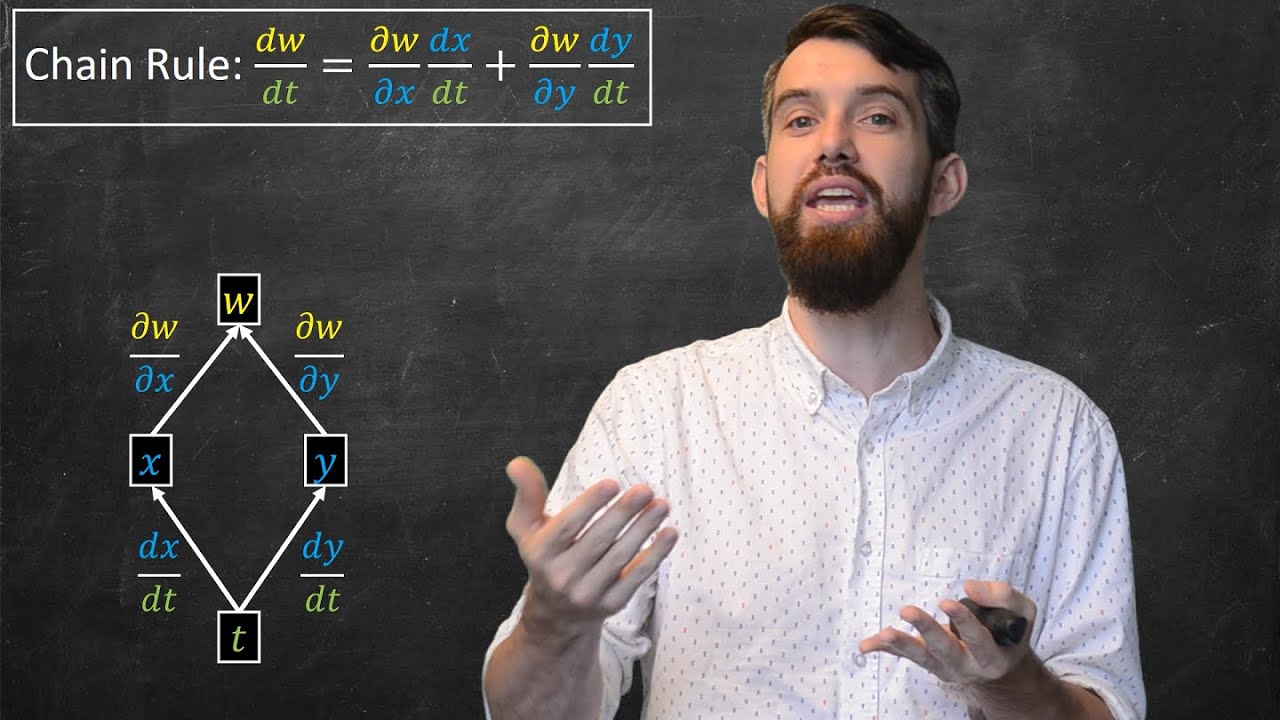
Multivariable chain rule
TLDRThe video script explores the concept of function composition and the derivative of a composite function, specifically focusing on the multivariable chain rule. It begins with a multivariable function f(x, y) = x^2 * y and introduces two single-variable functions, x(t) and y(t). The presenter illustrates how to find the derivative of the composed function without using the multivariable chain rule, demonstrating the process through an example where x(t) = cos(t) and y(t) = sin(t). The script then reveals a pattern that leads to the multivariable chain rule, showing how the partial derivatives of f with respect to x and y, when multiplied by the derivatives of x(t) and y(t) with respect to t, respectively, yield the derivative of the composed function. The presenter concludes by noting that this simple example serves as an introduction to the more general form of the multivariable chain rule, which will be discussed in a subsequent video, providing a foundation for understanding function composition and derivatives in a multivariable context.
Takeaways
- 📚 The script discusses the concept of function composition, specifically focusing on a multivariable function composed with single variable functions.
- 🔢 The multivariable function given has two variable inputs (x, y) and a single variable output, defined as x squared times y.
- 🎢 The composition of functions is visualized as moving a single point in 't' space to two-dimensional space (x, y) and then applying the multivariable function.
- 📈 The derivative of the composed function is sought, which is an ordinary derivative, not a partial derivative, since the final output is a single variable function.
- ⛓ The chain rule is mentioned as a special rule for derivatives of composed functions, but the script argues it's not necessary for this specific computation.
- 🔑 The process of finding the derivative involves substituting x(t) with cosine(t) and y(t) with sine(t), and then applying the definition of the multivariable function.
- 🧮 The product rule is used to find the derivative, which involves differentiating both the 'left' and 'right' parts of the composed function.
- 📌 The script highlights that the pattern observed in the derivative computation leads to the multivariable chain rule, even though it's derived from a single variable perspective.
- 📐 The partial derivatives of the multivariable function are discussed, showing how they relate to the components of the composed function's derivative.
- 🔍 The script rewrites the derivative to make the pattern clearer and to show the connection between the partial derivatives and the ordinary derivatives of the intermediary functions.
- 🌐 The multivariable chain rule is introduced as a generalization of the pattern observed, which is applicable to more complex scenarios involving multiple dimensions.
- 📝 The final takeaway is an anticipation of a future discussion on the intuition and formal reasoning behind the multivariable chain rule, including a more generalized form and vector notation.
Q & A
What is the first function described in the transcript?
-The first function is a multivariable function with two variable inputs, x and y, and a single variable output, which is the product of x squared and y.
How does the transcript describe the process of function composition?
-The transcript describes function composition by taking a single variable t, mapping it through two intermediary functions to obtain x(t) and y(t), and then applying a multivariable function f to these results.
What is the Chain Rule mentioned in the transcript?
-The Chain Rule mentioned is a special rule used to find the derivative of a composite function. In this context, it refers to the multivariable chain rule, which is used for functions with multiple variables.
Why does the transcript suggest that the multivariable chain rule is not needed for this particular computation?
-The transcript suggests that the multivariable chain rule is not needed because the computation can be done without it, even though it is a useful theoretical tool for understanding function composition in the multivariable world.
What is the role of the single variable chain rule in the derivative computation described?
-The single variable chain rule is used to find the derivative of the composition of functions. It is applied when taking the derivative of the outside function with respect to the inside function, which in this case is represented by the derivatives of x(t) and y(t) with respect to t.
How does the transcript illustrate the pattern leading to the multivariable chain rule?
-The transcript illustrates the pattern by showing the computation of the derivative of a composed function. It points out that the final result includes terms that correspond to the partial derivatives of the multivariable function f with respect to each of its variables, multiplied by the derivatives of the corresponding single variable functions.
What is the significance of rewriting the derivative expression in the transcript?
-Rewriting the derivative expression helps to clarify the pattern that emerges, which resembles the multivariable chain rule. It makes it easier to see how the partial derivatives of the multivariable function and the derivatives of the single variable functions combine to form the derivative of the composed function.
What are the partial derivatives of the multivariable function f with respect to x and y?
-The partial derivative of f with respect to x, treating y as a constant, is 2x. The partial derivative with respect to y, treating x as a constant, is simply the value of x squared, since y is treated as a constant multiplier.
How does the transcript generalize the result for the derivative of the composition?
-The transcript generalizes the result by stating that the derivative of the composition is the sum of the product of the partial derivative of f with respect to x and the derivative of x(t) with respect to t, and the product of the partial derivative of f with respect to y and the derivative of y(t) with respect to t.
What is the simplest form of the multivariable chain rule described in the transcript?
-The simplest form of the multivariable chain rule described is taking the ordinary derivative with respect to t of a composition of a multivariable function, where you multiply the partial derivative of the multivariable function with respect to each variable by the derivative of the corresponding single variable function with respect to t, and then sum these products.
What will be discussed in the next video according to the transcript?
-In the next video, the speaker will discuss the intuition behind why the multivariable chain rule is true, provide a more generalized form of the rule, and possibly use vector notation to make the presentation cleaner and more formal.
Outlines
📚 Understanding Function Composition and the Chain Rule
The first paragraph introduces three different functions: a multivariable function with two inputs (x, y) and a single output (x squared times y), and two single variable functions. The focus is on the composition of these functions, particularly using x(t) and y(t) as the components for the multivariable function f. The concept of t moving through a number line to a two-dimensional space and then being transformed by the multivariable function is discussed. The goal is to find the derivative of this composition, which is a single variable function, and the special rule for this, the chain rule, is mentioned. The paragraph walks through an example using cosine(t) for x(t) and sine(t) for y(t), applying the product rule and the single variable chain rule to find the derivative. It concludes by hinting at how this pattern leads to the multivariable chain rule, which will be explored further in subsequent content.
🔍 Observing Partial Derivatives and the Multivariable Chain Rule
The second paragraph delves into the partial derivatives of the multivariable function f with respect to x and y, treating one variable as constant while differentiating with respect to the other. It shows how these partial derivatives and the ordinary derivatives of the intermediary functions (x(t) and y(t)) with respect to t are related to the final result obtained from the derivative of the composed function. The paragraph highlights a pattern that emerges from these calculations, which aligns with the components of the multivariable chain rule. It concludes by stating the multivariable chain rule formula for the derivative of a composition of a multivariable function with respect to t, which involves taking partial derivatives and multiplying them by the derivatives of the intermediary functions with respect to t. The speaker expresses intent to discuss the intuition behind this rule and its more generalized form in the next video.
Mindmap
Keywords
💡Multivariable Function
💡Function Composition
💡Chain Rule
💡Derivative
💡Partial Derivative
💡Product Rule
💡Ordinary Derivative
💡Cosine and Sine Functions
💡Trigonometric Functions
💡Vector Notation
💡Single Variable Chain Rule
Highlights
Introduction of a multivariable function with two variable inputs, x and y, and a single variable output.
Explanation of composing functions, where the first component is the value of the function x(t) and the second is y(t).
Visualization of the function composition process, moving from a single variable t to two-dimensional space and then back to a single output.
Derivation of the composed function using an ordinary derivative, not a partial derivative, due to the single variable input and output.
Application of the chain rule in the context of a single variable function, which will lead to the multivariable chain rule.
Substitution of x(t) with cosine(t) and y(t) with sine(t) to find the derivative of the composed function.
Use of the product rule to find the derivative, emphasizing the pattern that leads to the multivariable chain rule.
Rewriting of the derivative to clarify the pattern and connection to the partial derivatives of the multivariable function f.
Observation that the pattern in the derivative matches the partial derivatives of f with respect to x and y.
Derivation of the ordinary derivatives of the intermediary functions x with respect to t and y with respect to t.
Generalization of the derivative of the composition to the multivariable chain rule formula.
Presentation of the multivariable chain rule formula, showing how it is derived from the partial derivatives and ordinary derivatives.
Explanation that the multivariable chain rule is applicable even for simple examples starting from one dimension and moving to two dimensions.
Promise of a future discussion on the intuition behind the multivariable chain rule and its more generalized form.
Mention of using vector notation to make the multivariable chain rule appear cleaner and more formal in future discussions.
Teaser for the next video, which will delve into a more formal argument for the multivariable chain rule's validity.
Transcripts
Browse More Related Video
The Multi-Variable Chain Rule: Derivatives of Compositions

find x' for the function x(t) defined implicitly. derivative of implicit function class 12

Partial derivatives - How to solve?

Multivariable chain rule and directional derivatives
dy/dx, d/dx, and dy/dt - Derivative Notations in Calculus

Exponential functions differentiation | Advanced derivatives | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: