BusCalc 17 Critical Points
TLDRThe video script discusses the concepts of increasing and decreasing functions, as well as critical points. It explains that the output values of a function determine whether it is increasing or decreasing as we read from left to right. The script uses a red function as an example of an increasing function, where the output values rise as we move from left to right. It also mentions a blue function that has intervals of both increase and decrease, highlighting that functions can exhibit both behaviors. The concept of critical points is introduced as points where the function neither increases nor decreases, often signifying a change in the function's direction. The script defines a function as increasing if its derivative is positive and decreasing if the derivative is negative. It further clarifies that a function is strictly increasing if it only ever increases and strictly decreasing if it only ever decreases. The video also demonstrates how to find critical points by taking the derivative of a function and setting it to zero. The summary concludes by emphasizing that if a function's derivative is continuous, it must pass through a critical point whenever it changes direction, which is a key takeaway for understanding the behavior of functions.
Takeaways
- 📈 A function is considered increasing when its derivative is positive, indicating that the output values are increasing as you move from left to right.
- 📉 Conversely, a function is decreasing when its derivative is negative, meaning the output values decrease as you move from left to right.
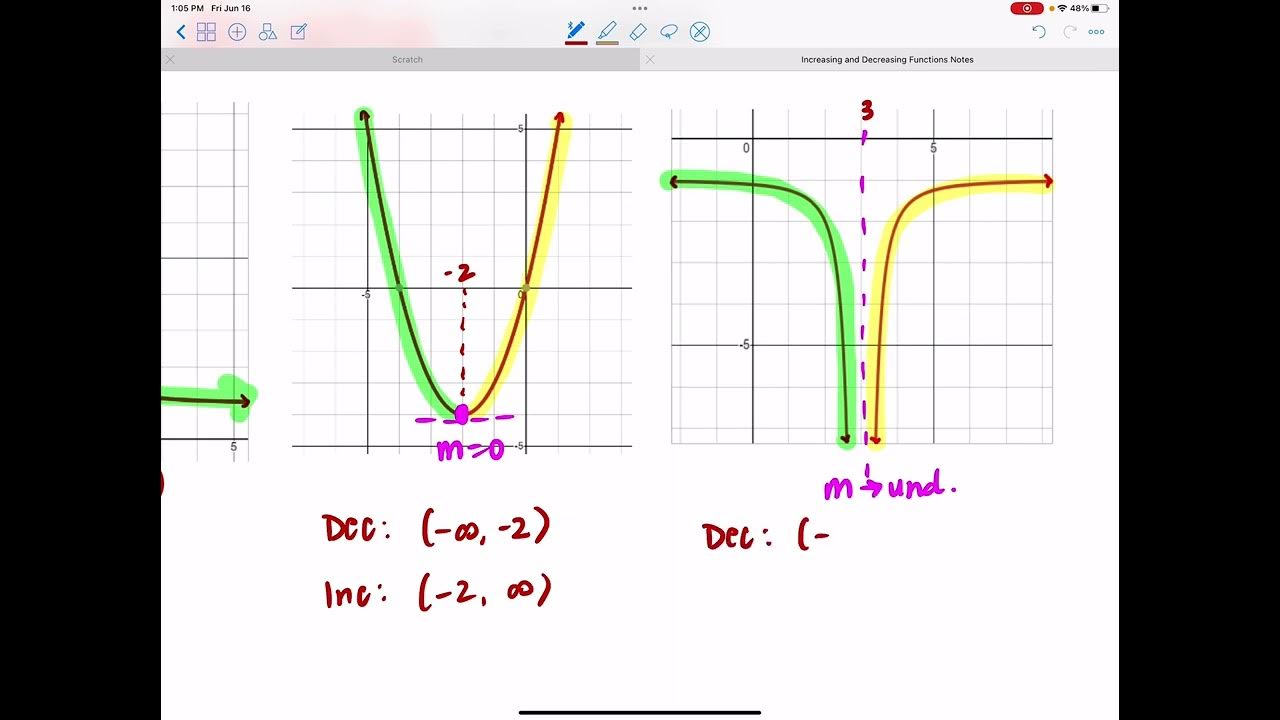
- 🔍 Critical points occur where a function changes from increasing to decreasing or vice versa, and they are identified when the derivative of the function is zero.
- 📌 At critical points, the function is neither increasing nor decreasing, representing a transition in the function's behavior.
- 🚫 A function is strictly increasing if it only ever increases and never decreases, which requires the derivative to be positive for all points in its domain.
- 🚫 A function is strictly decreasing if it only ever decreases and never increases, necessitating a negative derivative for all points in its domain.
- 🔢 To determine if a function is increasing or decreasing, one must examine the sign of its derivative.
- 🧮 The derivative of a function can be found using various rules such as the power rule or the quotient rule, depending on the function's form.
- 🌐 The sign of the derivative (positive or negative) directly correlates with the behavior (increasing or decreasing) of the function.
- ∞ An exponential function always has positive values, and when it is part of a fraction, it contributes to the overall sign of the derivative if the denominator is also positive.
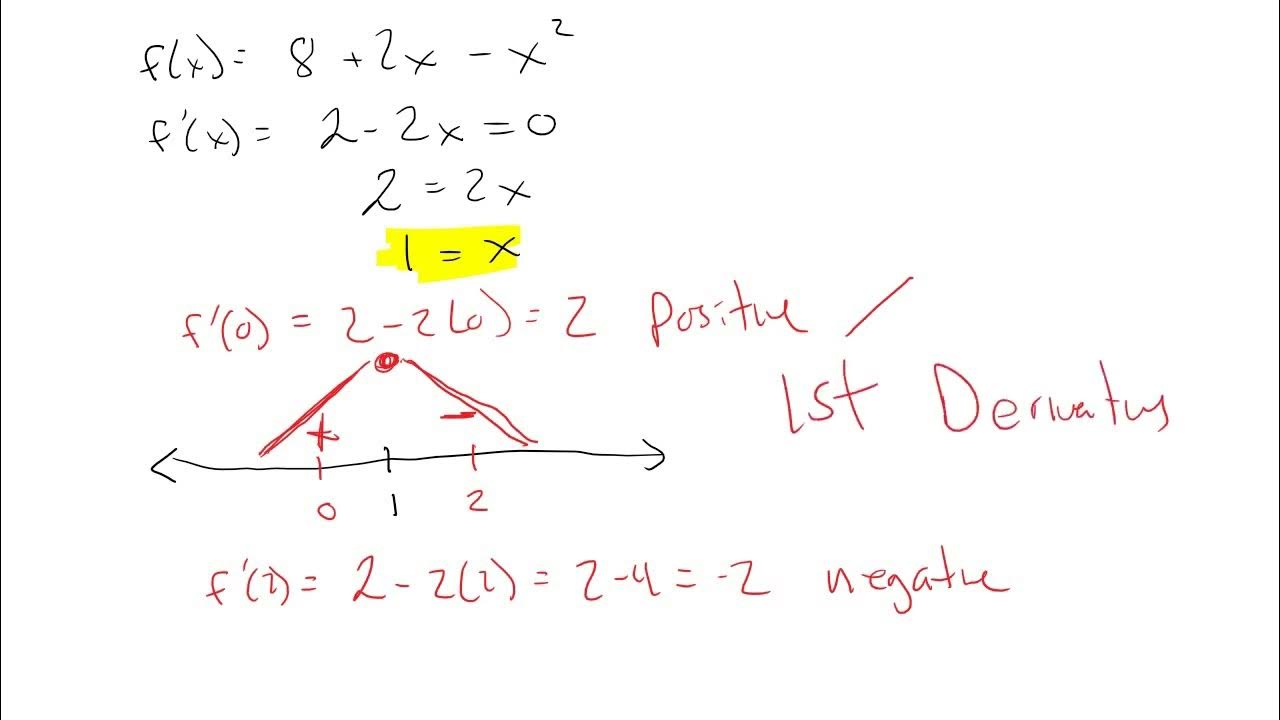
- 🔑 To locate critical points, take the derivative of the function and set it equal to zero, then solve for the variable to find the x-values where the function's behavior changes.
Q & A
What does the term 'increasing function' refer to in the context of the video?
-An 'increasing function' refers to a function whose output values increase as we read from left to right on a graph. This is determined by the positive value of the function's derivative at a given point.
How can you identify if a function is decreasing?
-A function is identified as decreasing when its output values decrease as we move from left to right on the graph. This corresponds to the function's derivative being negative at that point.
What is a critical point in a function?
-A critical point is a location on the graph of a function where the function is neither increasing nor decreasing. This occurs where the derivative of the function is zero or undefined.
What is the significance of the derivative being positive in determining the behavior of a function?
-A positive derivative indicates that the function is increasing at that point. It signifies that the slope of the tangent line to the graph of the function is positive, which means the function values are rising as we move from left to right.
How does the derivative being negative relate to the behavior of a function?
-A negative derivative indicates that the function is decreasing at that point. It means the slope of the tangent line to the graph of the function is negative, so the function values are falling as we move from left to right.
What does it mean for a function to be strictly increasing?
-A function is strictly increasing if it only ever increases and never decreases. This means that its derivative is positive for all points in its domain.
What does it mean for a function to be strictly decreasing?
-A function is strictly decreasing if it only ever decreases and never increases. This implies that its derivative is negative for all points in its domain.
How can you determine the critical points of a function?
-To determine the critical points of a function, you first find the derivative of the function. Then, you set the derivative equal to zero and solve for the variable to find the x-values where the function is neither increasing nor decreasing.
What is the role of the derivative quotient rule in finding the derivative of a function?
-The derivative quotient rule, also known as the quotient rule, is used to find the derivative of a function that is the quotient of two other functions. It is a formula that allows you to compute the derivative of such a quotient without having to expand and simplify the expression first.
Why is the value of the exponential function always positive?
-The exponential function, often denoted as e^x, is always positive because the base e (Euler's number) is a positive constant, and any power of a positive number is also positive. Thus, the exponential function only takes positive values for any real number x.
What is the relationship between a function's critical points and its behavior of increasing or decreasing?
-A function's critical points are the points at which the function transitions from increasing to decreasing or vice versa. If the derivative is continuous, it must pass through zero at a critical point whenever the function changes direction.
How does the sign of the denominator in the derivative expression affect the overall sign of the derivative?
-The sign of the denominator in a derivative expression, especially when raised to a power (like the square in the script), ensures that it is positive, as squaring any real number results in a positive value. This affects the overall sign of the derivative, especially when determining whether the function is increasing or decreasing.
Outlines
📈 Understanding Increasing and Decreasing Functions
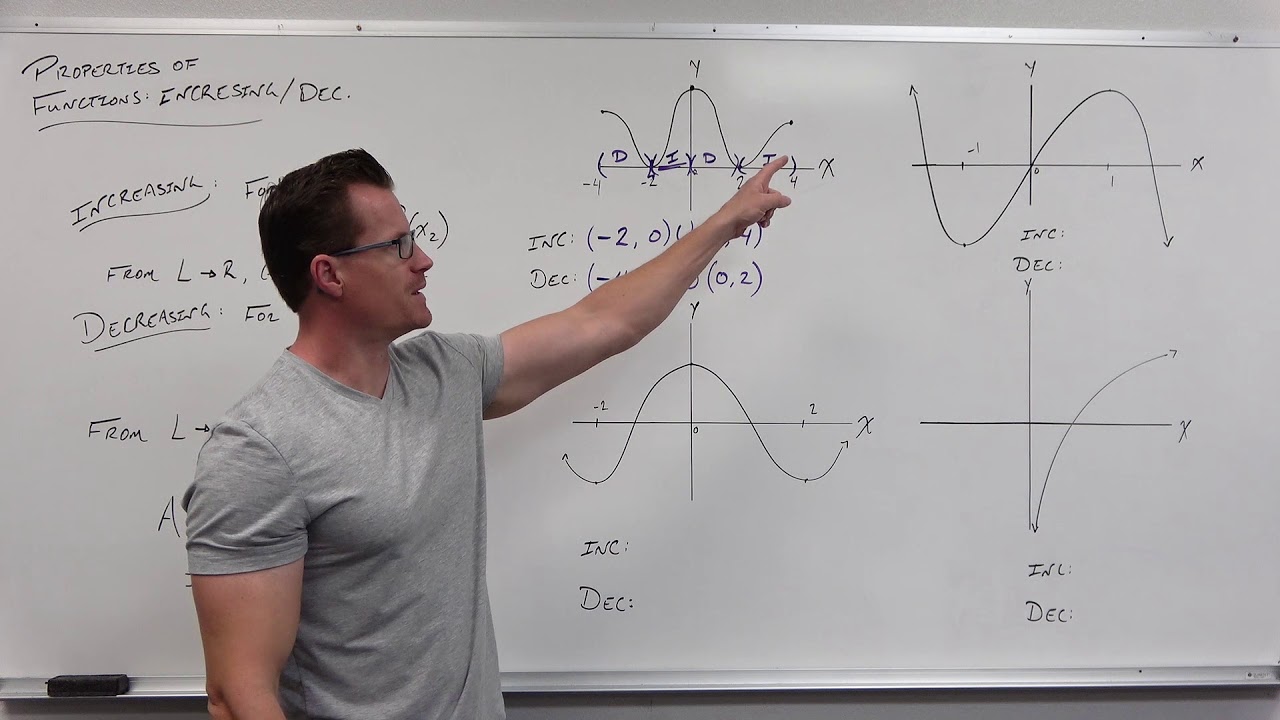
This paragraph introduces the concepts of increasing and decreasing functions, which are determined by the output values of a function as we read from left to right. It uses the red function as an example of an increasing function, where the output values increase as we move horizontally from left to right. The blue function is used to illustrate a function that can be both increasing and decreasing over different intervals. The concept of critical points is also introduced, which are points where the function is neither increasing nor decreasing. Critical points are important for understanding changes in the behavior of a function.
📉 Critical Points and Derivatives
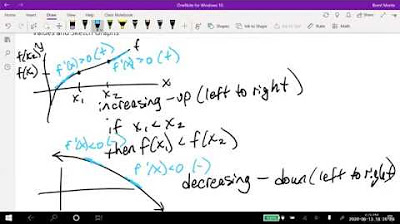
This paragraph delves into the mathematical definitions related to increasing and decreasing functions. It explains that a function is increasing if its derivative is positive, which indicates a positive steepness or slope at a given point. Conversely, a function is decreasing if its derivative is negative. The concept of strictly increasing and strictly decreasing functions is also discussed, where a function only ever increases or decreases without any change in direction. The red function from the previous paragraph is revisited, and its derivative is shown to be always positive, confirming it as a strictly increasing function. The blue curve is then analyzed, and it is shown that the function has two critical points where the derivative equals zero, indicating a change in the function's direction of increase or decrease.
Mindmap
Keywords
💡Increasing function
💡Decreasing function
💡Critical points
💡Derivative
💡Positive derivative
💡Negative derivative
💡Strictly increasing
💡Strictly decreasing
💡Continuous derivative
💡Quotient rule
💡Exponential function
Highlights
The concepts of increasing and decreasing functions and critical points are discussed.
Increasing functions have output values that increase as you read from left to right.
Decreasing functions have output values that decrease as you read from left to right.
A function can be increasing over some intervals and decreasing over others.
Critical points are where a function is neither increasing nor decreasing.
A function is increasing if its derivative is positive.
A function is decreasing if its derivative is negative.
A function is strictly increasing if it only ever increases and never decreases.
A function is strictly decreasing if it only ever decreases and never increases.
The red curve is an example of a strictly increasing function with a positive derivative everywhere.
The numerator and denominator of the derivative determine if it is positive or negative.
The exponential function has only positive values and approaches y=0 as x approaches negative infinity.
A point is a critical point if the derivative of the function is zero.
To find critical points, take the derivative, set it equal to zero, and solve for x.
The blue curve has two critical points at x = -1 and x = 1 where the derivative is zero.
If a function has a continuous derivative, it must pass through a critical point whenever it changes direction from increasing to decreasing or vice versa.
The video provides a clear explanation of key calculus concepts with helpful visual examples.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: