Calculus AB/BC – 4.2 Straight-Line Motion: Connecting Position, Velocity, and Acceleration
TLDRIn this engaging calculus lesson, Mr. Bean delves into the crucial concepts of position, velocity, and acceleration, which are fundamental to understanding motion and are often featured on AP exams. The video begins with a practical example of a tennis ball being thrown straight up, illustrating the position function and how it relates to the height of the ball over time. Mr. Bean then explains that velocity is the rate of change of position, and acceleration is the rate of change of velocity, emphasizing the importance of calculus in connecting these three elements. The lesson continues with a detailed exploration of how to determine if an object is speeding up or slowing down by examining the signs of velocity and acceleration. Mr. Bean also discusses the concept of average velocity and introduces the idea of displacement, which is the net change in position. The video concludes with a series of problems that challenge the viewer to apply these concepts to various scenarios, reinforcing the practical application of calculus in physics and problem-solving.
Takeaways
- 📚 **Importance of the Lesson**: This calculus lesson is ranked in the top five for its significance, particularly for AP exams.
- 📈 **Position, Velocity, and Acceleration**: Position is the height of an object over time. Velocity is the rate of change of position, and acceleration is the rate of change of velocity.
- ⏳ **Derivatives and Their Meanings**: The first derivative of position gives velocity, and the second derivative gives acceleration.
- 🔢 **Understanding Direction**: A negative velocity indicates movement to the left or downward, while a positive velocity indicates movement to the right or upward.
- 🧲 **Acceleration and Gravity**: The acceleration due to gravity is a constant -9.8 m/s², acting downward.
- 🏃 **Average Velocity Calculation**: Average velocity is the slope between two points on the position graph, calculated as the change in position divided by the change in time.
- 🛣️ **Speed vs. Velocity**: Speed is the absolute value of velocity and represents how fast an object is moving without considering direction.
- ↗️/↘️ **Direction of Motion**: An object speeds up when velocity and acceleration have the same sign and slows down when they have different signs.
- 🔁 **Displacement**: Displacement is the net change in position, which can be zero if an object returns to its starting point after moving.
- 📉 **Particle's Movement**: The particle's movement (left or right) can be determined by whether the velocity is negative or positive.
- 📚 **Practice and Mastery**: The concepts taught are fundamental and will be frequently used and tested throughout the course.
Q & A
What is the position function in the context of the script?
-The position function represents the height of a tennis ball thrown straight up in the air by Mr. Brust, as a function of time. It starts at a certain height (not on the ground), goes up, and then comes back down to the ground.
What is the relationship between velocity and position?
-Velocity is the rate of change of position. It is the derivative of the position function with respect to time.
How is acceleration related to velocity and position?
-Acceleration is the rate of change of velocity, which is the second derivative of the position function with respect to time.
What is the significance of the signs of velocity and acceleration in determining if a particle is speeding up or slowing down?
-If the velocity and acceleration have the same sign (both positive or both negative), the particle is speeding up. If they have different signs, the particle is slowing down.
How is speed different from velocity?
-Speed is the absolute value of velocity. It does not have a direction and only considers the magnitude of how fast an object is moving.
What is the formula for calculating average velocity?
-Average velocity is calculated as the change in position (s of b - s of a) divided by the change in time (b - a) over the interval from time a to time b.
What does the term 'displacement' represent in the context of the script?
-Displacement represents the net change in position of an object. It is the straight-line distance from the starting point to the final position, regardless of the path taken.
How does the script differentiate between a particle moving to the right and moving to the left?
-A particle is considered to be moving to the right when the velocity is positive (greater than zero), and it is moving to the left when the velocity is negative (less than zero).
What is the significance of the constant acceleration in the script?
-The constant acceleration in the script represents the acceleration due to gravity, which is negative in the context of an object being thrown upwards and then falling back down to the ground.
How does the script illustrate the concept of a particle being at rest?
-A particle is considered to be at rest when its velocity is zero, meaning it is not moving in any direction.
What is the role of calculus in connecting position, velocity, and acceleration?
-Calculus is used to connect position, velocity, and acceleration by taking derivatives of the position function with respect to time. The first derivative gives velocity, and the second derivative gives acceleration.
Outlines
📚 Introduction to Calculus Concepts
This paragraph introduces the audience to a crucial calculus lesson, emphasizing its importance in the AP exam. The teacher, Mr. Bean, uses the example of Mr. Brust playing catch with himself to illustrate the concepts of position, velocity, and acceleration. The position function is described, showing the path of a tennis ball thrown upwards. Velocity is explained as the rate of change of position, starting at a certain speed and slowing down until it reaches zero at the peak. Acceleration is introduced as the rate of change of velocity, exemplified by the constant acceleration due to gravity. The paragraph concludes by stressing the need to connect these three concepts using calculus.
🚀 Understanding Velocity and Acceleration
The second paragraph delves deeper into the relationship between velocity and acceleration. It explains that if both velocity and acceleration have the same sign, the object is speeding up, while different signs indicate the object is slowing down. The teacher shares a personal anecdote about skydiving to illustrate these concepts. The paragraph also covers the concept of average velocity, which is the slope between two points on the position graph, and the distinction between speed and velocity. Speed is the absolute value of velocity, indicating the magnitude of motion without a direction. Displacement is introduced as the net change in position, which can be zero if the starting and ending points are the same, even if the path taken is longer.
📉 Analyzing Graphs and Derivatives
This paragraph focuses on using calculus to analyze the motion of a particle along the x-axis. The position function is given, and the teacher demonstrates how to calculate displacement by finding the position at two different times and subtracting them. The concept of average velocity is further explained, and the derivative of position (velocity) is calculated at a specific time. The acceleration, as the second derivative of position, is also derived and evaluated at a particular time. The paragraph concludes with determining whether the particle is speeding up or slowing down based on the signs of velocity and acceleration.
🔍 Interpreting Velocity and Acceleration Graphs
The final paragraph deals with interpreting velocity and acceleration graphs to determine the motion of a particle. It explains that a particle moves to the right when the velocity is positive and to the left when the velocity is negative. The teacher guides the students through identifying intervals where the particle is moving in a particular direction based on the velocity graph. The concept of acceleration is also explored, with the teacher showing how to find intervals where the acceleration is positive, negative, or zero by examining the slope of the velocity graph. The paragraph concludes with determining the greatest speed of the particle, which is the highest absolute value of velocity, and identifying intervals where the particle is speeding up or slowing down based on the signs of velocity and acceleration.
Mindmap
Keywords
💡Calculus
💡Position Function
💡Velocity
💡Acceleration
💡Derivative
💡Rectilinear Motion
💡Average Velocity
💡Speed
💡Displacement
💡Sign of Velocity and Acceleration
💡Second Derivative
Highlights
Mr. Bean introduces one of the most important calculus lessons, emphasizing its significance in AP exams.
The lesson covers the concepts of position, velocity, and acceleration, which are fundamental to understanding motion.
Velocity is defined as the rate of change of position, with the derivative of position function representing velocity.
Acceleration is the rate of change of velocity, which is found by taking the second derivative of the position function.
The importance of understanding the direction of motion is highlighted, with positive and negative velocities indicating direction.
Average velocity is calculated as the slope between two points on the position graph, representing the average rate of change.
Speed is distinguished from velocity as the absolute value of velocity, indicating how fast an object is moving without direction.
The relationship between velocity and acceleration is used to determine if an object is speeding up or slowing down.
Mr. Bean shares a personal anecdote about skydiving to illustrate the concepts of velocity and acceleration in real-life experience.
Displacement is defined as the net change in position, which can be zero even if the path traveled is not.
The calculation of displacement involves finding the difference between the starting and ending positions.
The velocity of a particle at a specific time is found by taking the derivative of the position function and evaluating it at that time.
Acceleration can be determined by taking the second derivative of the position function, representing the rate of change of velocity.
The direction of particle motion (left or right) can be inferred from the sign of the velocity on a graph.
The particle's speed is greatest when the absolute value of velocity is the highest, regardless of direction.
The intervals during which the particle is speeding up or slowing down are determined by the signs of velocity and acceleration.
Mr. Bean emphasizes the importance of understanding the signs of velocity and acceleration for determining motion dynamics.
The lesson concludes with a reminder to practice these concepts as they are frequently tested in AP calculus exams.
Transcripts
Browse More Related Video
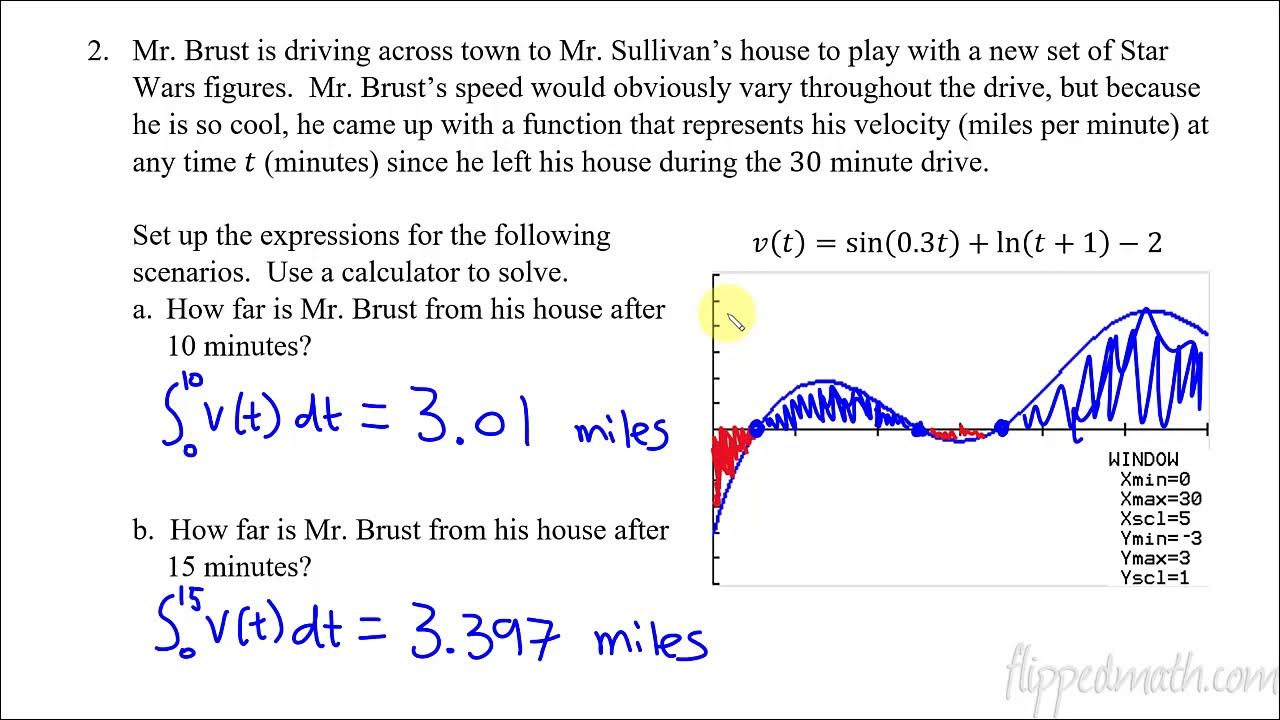
Calculus AB/BC – 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals

Calculus AB/BC – 4.3 Rates of Change in Applied Contexts Other Than Motion

Calculus - Position Average Velocity Acceleration - Distance & Displacement - Derivatives & Limits
Position, Velocity, and Acceleration vs. Time Graphs
13 - Instantaneous Acceleration Explained (Average Vs. Instantaneous Acceleration)

Position, Velocity, Acceleration using Derivatives
5.0 / 5 (0 votes)
Thanks for rating: