AP Calculus BC Practice Exam 2012 - Calculator Multiple Choice questions 76-92

vinteachesmath

30 Apr 202142:41

EducationalLearning

32 Likes 10 Comments

TLDRThe video transcript details a comprehensive review of the 2012 AP Calculus BC multiple-choice section, focusing on various calculus concepts. The speaker, Van, methodically approaches each question, starting with question 76, where he discusses the continuity, differentiability, and concavity of a given function f. He employs the concept of derivatives to analyze the rate of change and uses a graphing calculator to determine intervals of interest. The video continues with an evaluation of definite integrals, the application of Taylor polynomials, and the exploration of the average value of functions. It delves into the limit definition of continuity, the calculation of fuel consumption rates in related rates problems, and the use of derivatives to determine the concavity of functions. The speaker also addresses the concept of the first derivative, definite integrals, and the volume of solids generated by polar curves. The video concludes with a discussion on series convergence, the fundamental theorem of calculus, and the application of Cavalieri's principle. Throughout the script, Van emphasizes the importance of understanding calculus principles and applying them effectively to solve complex problems, providing a valuable resource for students preparing for AP Calculus exams.

Takeaways

📈 For question 76, the key to solving the problem was to identify the false statement about the function f, which was determined by analyzing the graph's continuity, differentiability, and behavior at x=0.
📊 Question 77 involved comparing the rate of change of two functions, f(x) and g(x), by graphing them and finding the intervals where one function's rate of change was greater than the other's.
🧮 In question 78, the calculation of a definite integral for a piecewise function required breaking the integral into parts and using geometry to find the area under the curve.
📚 Question 79 focused on the Taylor polynomial, specifically the third-degree polynomial centered at x=3, which required knowledge of derivatives and factorials.
🔍 For question 80, the strategy involved analyzing the graph of the first derivative to determine the presence of a relative minimum, a point of inflection, and concavity.
📐 Question 81 required understanding the relationship between the function's even nature and its graph, which influenced the location of points of inflection.
💡 Question 82 dealt with finding the average value of a function over an interval, which is calculated using the integral of the function divided by the width of the interval.
🔑 For question 83, the concept of continuity was applied, focusing on the limit definition and how it relates to the function's behavior at a specific point.
📉 Question 84 involved finding intervals where the graph of a function was concave down, which was determined by analyzing the second derivative of the function.
🚗 Question 85 was a related rates problem that required applying the chain rule to find the rate of change of fuel consumption in relation to the speed of a car.
⛰ Question 86 examined the concept of a function that is always increasing and how it relates to the definite integral being equal to zero over an interval.
🏗️ Question 87 utilized Cavalieri's principle to find the volume of a solid generated by revolving a region bounded by a curve around an axis.
📌 Question 88 required analyzing the behavior of a function based on the information about its derivative and second derivative to determine the shape of the graph.
🚀 Question 89 applied the fundamental theorem of calculus to find the velocity of a particle at a given time, given its acceleration function.
🔄 Question 90 involved series convergence, requiring comparison tests and understanding the behavior of series terms to determine which statements must be true.
⭕ Question 91 was a challenging problem involving the area of polar curves, specifically finding the area of a circle minus the area of three petals of a rose curve.

Q & A

What is the correct answer for question 76 in the 2012 Calc BC Calculator section?
-The correct answer for question 76 is B, indicating that the function f is not differentiable at zero due to a sharp turn at x equals zero.
How does the speaker determine the intervals where the rate of change of f(x) is greater than the rate of change of g(x) in question 77?
-The speaker uses a graphing calculator to plot both functions f(x) = e^x and g(x) = 4x^3. By observing where the graph of f(x) is above g(x), the speaker identifies the intervals from negative infinity to 0.831 and from 7.384 to positive infinity where the rate of change of f(x) is greater than that of g(x).
What is the method used to evaluate the definite integral in question 78?
-The method used involves breaking up the integral into two parts, using basic geometry to calculate the area under straight line segments, and applying the fundamental theorem of calculus to evaluate the antiderivative of the function over the given interval.
What is the general form of a third-degree Taylor polynomial centered at x=3, as discussed in question 79?
-The general form of a third-degree Taylor polynomial centered at x=3 is f(3) + f'(3)(x-3)/1! + f''(3)(x-3)^2/2! + f'''(3)(x-3)^3/3!.
How does the speaker approach the Roman numeral question (question 80) regarding the graph of f'?
-The speaker approaches the question by analyzing the given graph of f' to determine the sign changes of the first and second derivatives, which indicate relative minima, points of inflection, and concavity of the function f.
What is the strategy suggested for solving question 81, which involves the sine of f, f', and f''?
-The suggested strategy is to create a sine chart for f' and f'' over the given intervals, analyze the concavity and monotonicity of the function, and use the detail that f(x) = f(-x) to determine the x-coordinates of the points of inflection.
What is the formula for the average value of a function on an interval, as discussed in question 82?
-The formula for the average value of a function f(x) on the interval [a, b] is (1/(b-a))∫[a, b] f(x) dx.
How does the speaker determine the intervals for which the graph of f is concave down in question 83?
-The speaker determines the intervals by taking the derivative of f'(x) to find f''(x), then graphing f''(x) and identifying the intervals where f''(x) is less than zero.
What is the concept used to solve the related rates problem in question 85?
-The concept used is the chain rule from calculus, which allows the speaker to relate the rate of change of fuel consumption (df/dt) to the rate of change of speed (ds/dt) and the function f(s) that describes fuel consumption in terms of speed.
What is the reasoning behind the answer to question 86, which involves the first derivative and definite integrals?
-The reasoning is that since f'(x) is always positive, the function f is always increasing. The definite integral from 4 to 7 being zero implies that the area under the curve from 4 to 7 must cancel out to zero, which can only happen if there are equal and opposite areas on either side of the x-axis.
How does the speaker approach the Cavalieri's principle question (question 87) to find the volume of a solid?
-The speaker approaches the question by considering the solid as being made up of infinitely thin cross-sections perpendicular to the x-axis, each with a height equal to the function's value at that x-value. The volume is then found by integrating the squared function over the given interval.

Outlines

00:00

📈 Analyzing the 2012 Calc BC Calculator Multiple Choice Questions

The video begins with an introduction to the 2012 Calc BC Calculator Multiple Choice section, focusing on Question 76 which involves evaluating the truthfulness of statements about a given function's graph. The presenter discusses concepts like continuity, differentiability, critical points, absolute minimums, and concavity. The analysis proceeds to Question 77, which requires understanding the rate of change and the use of a graphing calculator to compare the derivatives of two functions. The presenter also covers how to evaluate definite integrals and the application of Taylor polynomials.

05:02

🧮 Solving Definite Integrals and Understanding Taylor Polynomials

The presenter breaks down how to evaluate a definite integral from a piecewise function, using basic geometry and the fundamental theorem of calculus. The explanation continues with the construction of a third-degree Taylor polynomial centered at a specific point, emphasizing the importance of knowing the general form and the coefficients involved. A Roman numeral question follows, which tests the understanding of relative minima and points of inflection, cautioning against common pitfalls in interpretation.

10:03

📊 Interpreting Graphs and Applying Sine Charts to Find Points of Inflection

The video delves into the use of sine charts to analyze the behavior of a function's first and second derivatives over specified intervals. The presenter illustrates how to sketch a graph and apply the property that a function is even, leading to the identification of points of inflection. The discussion highlights the importance of considering the function's symmetry and the implications for points of inflection at specific x-coordinates.

15:04

💡 Calculating Average Values and Applying Limit Definitions

The presenter explains how to find the average value of a function over an interval, demonstrating the process with an example involving the square root of cosine x. The explanation then moves to the limit definition of continuity, emphasizing the need to compare left and right limits and how they relate to the function's value at a point. The video continues with an exploration of concavity and how to use a calculator to find intervals where a graph is concave down.

20:07

🚗 Applying Related Rates and Understanding Increasing Functions

The video addresses a related rates problem involving fuel consumption in a car, showing how to use the chain rule to find the rate of change of fuel consumption with respect to speed. It also discusses the concept of a function that is always increasing, as indicated by a positive first derivative, and the implications for the definite integral over an interval. The presenter then guides viewers through evaluating a table of values to determine which functions are always increasing.

25:08

🏞️ Sketching Graphs and Visualizing Solids of Revolution

The presenter sketches the graph of the natural logarithm function and applies Cavalieri's principle to find the volume of a solid generated by revolving the region under the curve around the x-axis. The explanation involves setting up an integral that represents the volume of infinitely thin squares formed by cross-sections of the solid. The video concludes with the calculation of the volume and the corresponding answer choice.

30:08

📉 Examining the Behavior of a Function's Derivative and Second Derivative

The video explores the implications of a function's derivative increasing for x less than zero and decreasing for x greater than zero. The presenter translates this information into the behavior of the second derivative and sketches potential graphs that could satisfy these conditions. The explanation continues with the application of the fundamental theorem of calculus to find the velocity of a particle at a given time, given its acceleration function.

35:10

🔢 Convergence of Series and Multiplication of Sequences

The presenter discusses the properties of a series that converges with all positive terms, using the ratio test and direct comparison to evaluate which statements must be true. The explanation involves analyzing the behavior of the series when terms are multiplied by n and comparing it to a geometric series. The video concludes with the identification of the correct answer choice based on the analysis.

40:10

🌹 Finding the Area of a Rose Curve and a Circle

The video addresses a problem involving the area enclosed by a circle and a three-petaled rose curve. The presenter explains how to find the area of one petal using the correct limits and then multiplying by three for the total area of the petals. The area of the circle is subtracted from the area of the petals to find the sum of the shaded regions, leading to the correct answer choice.

🔍 Verifying Statements Using Derivatives

The presenter evaluates the truth of several statements about a function that is symmetrical around the vertical line x=1. By taking the derivative of the given function and applying it to the statements, the video demonstrates which statements must be true and which can be false using counterexamples. The explanation concludes with the identification of the only statement that is necessarily true.

Mindmap

Keywords

💡Continuous function

A continuous function is one that can be drawn without lifting the pen from the paper. In the video, it is used to describe the function f at x equals zero, which can be drawn in one motion through that point, indicating that option A is true.

💡Differentiable

A function is differentiable at a point if it has a derivative at that point. The video explains that function f is not differentiable at x equals zero due to a sharp turn, making option B the false statement in question 76.

💡Critical point

A critical point of a function occurs where the derivative is either zero or undefined. The video states that f has a critical point at x equals zero because the derivative is undefined at that point, which is within the domain of the function, making option C true.

💡Absolute minimum

An absolute minimum is a point on the graph of a function where the function value is the lowest. The video identifies that f has an absolute minimum at x equals zero, as it is the lowest point of the graph, which validates option D as true.

💡Concavity

Concavity refers to the curvature of a function's graph. The video discusses how the graph of f changes concavity at x equals zero, switching from concave down to concave up, which is an important feature to identify in option E as true.

💡Derivative

The derivative of a function at a point gives the rate of change of the function at that point. In the video, the concept of the derivative is used to determine intervals where the rate of change of one function is greater than another, as seen in question 77.

💡Definite integral

A definite integral represents the area under the curve of a function between two points. The video shows how to evaluate a definite integral for a piecewise function, which is broken down into simpler shapes to calculate the area, as demonstrated in question 78.

💡Taylor polynomial

A Taylor polynomial is an approximation of a function near a given point using derivatives of the function. The video explains how to construct a third-degree Taylor polynomial for a function f about x equals three, which involves using the function's derivatives at that point, as seen in question 79.

💡Relative minimum

A relative minimum is a point on the graph of a function where the function value is the lowest among neighboring points. The video uses the concept to determine if f has a relative minimum at x equals negative three by checking the sign change of the first derivative, which is part of a Roman numeral question.

💡Point of inflection

A point of inflection is a point on the graph of a function where the concavity changes. The video discusses how to identify points of inflection by examining the sign changes of the second derivative or the slope of the first derivative's graph, as explored in question 81.

💡Average value

The average value of a function over an interval is a measure that describes the central tendency of the function's values over that interval. The video demonstrates how to calculate the average value of a function on a given interval using the formula provided, as shown in question 82.

💡Limit definition of continuity

The limit definition of continuity states that a function is continuous at a point if the limit of the function as x approaches that point is equal to the function's value at that point. The video uses this definition to evaluate the continuity of a function at x equals three in question 83.

💡Second derivative

The second derivative of a function gives information about the function's concavity. The video explains how to find intervals where a graph is concave down by determining where the second derivative is less than zero, as illustrated in question 84.

💡Related rates

Related rates problems involve finding the rate at which one quantity changes in relation to another. In the video, a related rates question about the fuel consumption of a car is solved by using the chain rule and the given rate of change of speed to find the rate of change of fuel consumption, as seen in question 85.

💡First derivative

The first derivative of a function indicates the slope of the function at a point and can tell us if the function is increasing or decreasing. The video uses the first derivative to analyze the behavior of a function over an interval, as shown in question 86.

💡Cavalieri's principle

Cavalieri's principle is a method in geometry that uses cross-sections to determine the volume of objects with the same cross-sectional area. The video applies this principle to find the volume under a curve between the x-axis and a function, as demonstrated in question 87.

💡Fundamental theorem of calculus

The fundamental theorem of calculus connects differentiation and integration, stating that the definite integral of a function's derivative is equal to the function's difference over the interval. The video uses this theorem to find the velocity of a particle at a given time, as shown in question 89.

💡Series convergence

A series is said to converge if the sum of its terms approaches a finite value. The video discusses the properties of a series that converges and uses comparison tests to evaluate the behavior of related series, as seen in question 90.

💡Polar coordinates

Polar coordinates are a two-dimensional coordinate system where each point is determined by a distance from a reference point and an angle from a reference direction. The video uses polar coordinates to find the area of a region bounded by a circle and a rose curve, as shown in question 91.

Highlights

The video discusses the 2012 Calculus BC Calculator section, providing a comprehensive walkthrough of multiple-choice questions.

Question 76 analysis focuses on the continuity and differentiability of a function, using a graph to determine true or false statements.

For question 77, the concept of the rate of change is explored, comparing the derivatives of two functions to find intervals where one exceeds the other.

Question 78 involves evaluating a definite integral of a piecewise function, using geometry and the fundamental theorem of calculus.

Question 79 requires knowledge of Taylor polynomials, specifically the third-degree polynomial centered at x equals three.

The video explains how to approach true/false questions systematically by analyzing the properties of a function's derivative, as seen in question 80.

Question 81 deals with the sine of a function's first and second derivatives, using a sine chart to determine points of inflection.

The average value of a function on a given interval is calculated using the average value formula, demonstrated in question 82.

The limit definition of continuity is applied to determine intervals where a graph is concave down, as shown in question 83.

Question 84 is a related rates problem involving fuel consumption in relation to a car's speed, using the chain rule to find the rate of change.

The concept of a function always increasing, as indicated by a positive first derivative, is used to solve question 85.

Cavalieri's principle is applied to find the volume of a solid formed by cross-sections in question 86.

The behavior of a function's derivative and second derivative is analyzed to determine the graph's shape in question 87.

The fundamental theorem of calculus is used to find the velocity of a particle from its acceleration function in question 88.

Question 89 involves a series convergence test, where the ratio test is used to evaluate the series' behavior.

The area of a region bounded by two polar curves is calculated in question 90, using the correct limits of integration.

The final question, a Roman numeral question, requires the use of derivatives to verify the truth of given statements about a function's symmetry.

Transcripts

Browse More Related Video

AP Calculus BC 2003 Multiple Choice (calculator) - Questions 76 - 92

AP Calculus AB 2012 Multiple Choice (calculator) - Questions 76 - 92

AP Calculus AB 2008 Multiple Choice (Calculator) - Questions 76-92

AP Calc AB & BC Practice MC Review Problems #6

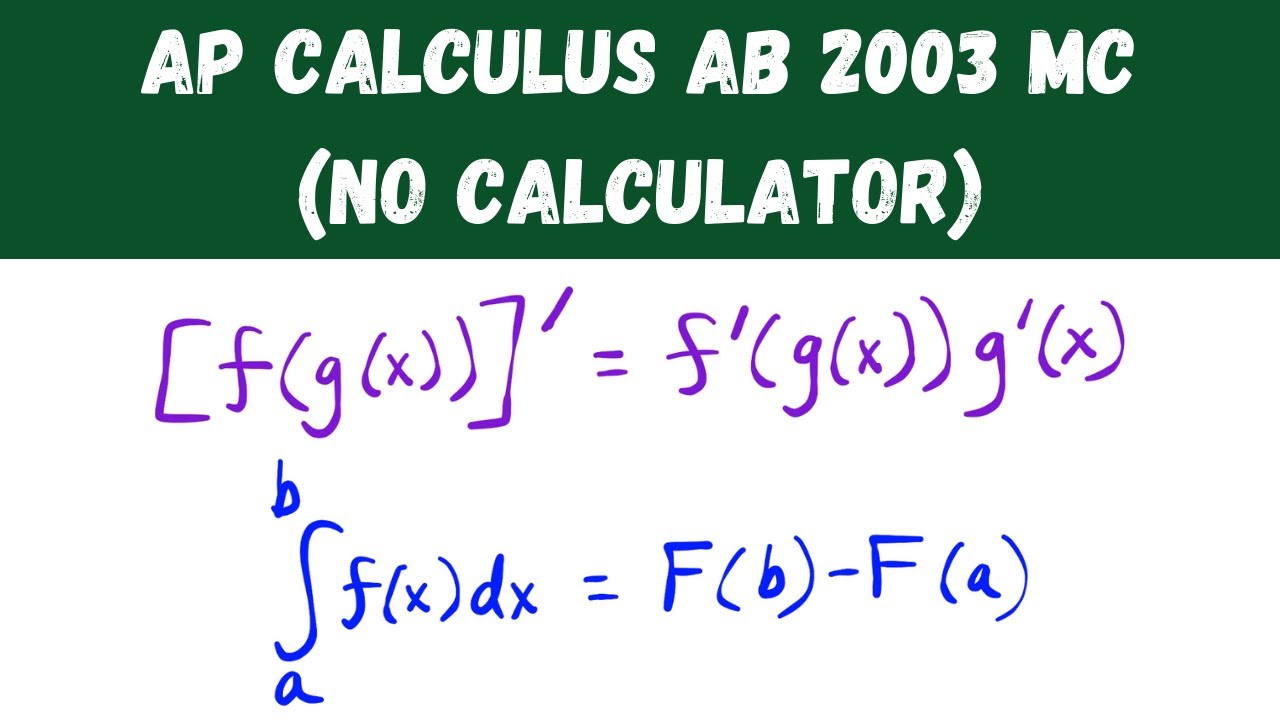
AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28

AP Calculus AB 1998 Multiple Choice No Calculator

Related Tags

AP Calculus Multiple Choice Graph Analysis Derivatives Integrals Series Convergence Math Education Problem Solving Exam Preparation Educational Video Calculus Tutorial