AP Calculus BC 2003 Multiple Choice (calculator) - Questions 76 - 92
TLDRThe video script is a comprehensive walkthrough of the 2003 AP Calculus BC multiple-choice section, specifically the calculator portion. The presenter, Van, meticulously guides viewers through various calculus problems, emphasizing the importance of understanding fundamental concepts such as limits, derivatives, integrals, and the application of the chain rule. He covers a range of topics, including the evaluation of Taylor polynomials, related rates, and the use of Cavalieri's principle for calculating volumes. Van also highlights the significance of the Mean Value Theorem and demonstrates how to apply it to find specific values of functions. Throughout the session, he uses a calculator to solve complex problems, showcasing the process of finding antiderivatives, evaluating integrals, and differentiating functions. The script concludes with a focus on the application of calculus in real-world scenarios, such as determining the height of an object at its maximum upward velocity. This detailed analysis serves as an invaluable resource for students preparing for AP Calculus exams, providing insights into problem-solving strategies and the practical use of calculus in various contexts.
Takeaways
- 📈 Understanding the concept of limits and continuity is crucial for calculus problems, as demonstrated in question 76 where the existence of a limit does not guarantee the function's continuity at that point.
- 🔢 Memorizing Taylor polynomial formulas is key for problems like question 77, where knowing the formula for the third derivative at zero allows you to find the value of the function's third derivative.
- 🔄 Mastering the chain rule is essential, as seen in question 78, where it's used to find the rate of change of the area of a circle with a changing radius.
- 📚 Familiarity with integrals and rates, as in question 80, is important for calculating net changes, such as the total amount of crops destroyed by insects over a period of time.
- 🧮 Using a graphing calculator efficiently, as shown in question 81, can help find limits and perform other complex calculations by visualizing the function's behavior.
- 🏞️ Recognizing the implications of concavity and monotonicity on approximation methods, as in question 85, is vital for determining the accuracy of trapezoidal and Riemann sums.
- 🔑 The mean value theorem, as discussed in question 83, guarantees the existence of a point where the instantaneous rate of change equals the average rate over an interval, provided the function is continuous and differentiable.
- 📏 Points of inflection, covered in question 86, are identified by finding where the second derivative changes sign, which requires both calculation and graphing.
- ⏱️ For related rates problems like question 87, it's important to recognize that the integral of the rate gives the net change, which can be used to find quantities like position at a specific time.
- 🏗️ Cavalieri's principle, used in question 89, allows the calculation of volumes by considering the area of cross-sections, particularly useful for complex shapes.
- 📉 The concept of integrals representing the area under a curve, as in question 90, is fundamental for finding the net change in a function over an interval.
Q & A
What is the key concept Van is trying to convey in the first question regarding the function f?
-The key concept is to identify a statement that must be false based on the graph of the function f. Van explains that while the existence of f(a) and the function being defined from 0 to a are true, the statement that must be false is about the limit of f as x approaches a and the continuity of the derivative at x equals a.
How does Van approach the Taylor polynomial question (Question 77)?
-Van approaches the Taylor polynomial question by first reminding the viewer of the formula for a Taylor polynomial centered at zero and then identifying the term associated with the third derivative in the polynomial. He then uses algebra to solve for the third derivative at zero, f'''(0), which is a crucial step in finding the correct answer.
What is the main strategy Van uses to solve the related rates problem (Question 78)?
-Van's main strategy is to use the given information about the radius of the circle increasing at a constant rate to find the rate of increase in the area. He employs the chain rule to differentiate the area formula with respect to time and then uses the given circumference to find the rate of change of the area.
How does Van determine the answer to the question about the chain rule (Question 79)?
-Van uses the chain rule formula to find the derivative of a composite function. He identifies the outer function and its derivative, as well as the inner function and its derivative, and then multiplies them together to find the overall derivative at a specific point, which leads him to the correct answer.
What is the integral concept Van emphasizes for the question about insects destroying crops (Question 80)?
-Van emphasizes the concept that the integral of the rate tells you the net change of the function. He applies this concept by integrating the given rate function over a specific time interval to find out how many tons of crops were destroyed by the insects.
How does Van use the graph to find the limit in Question 81?
-Van uses the graph to identify the behavior of the function f as x approaches 1. He observes the graph to determine the limit of f(x) as x approaches 1, which is indicated by the value of the function at the open circle on the graph, and then calculates the sine of that value to find the answer.
What is the main concept Van discusses in Question 82 regarding the rate of change of the altitude of a hot air balloon?
-The main concept Van discusses is finding the exact times when the altitude is decreasing by determining where the rate function, r(t), is less than zero. He uses the calculator to find the time intervals where the altitude decreases and uses these intervals as the limits of integration to find the change in altitude.
How does Van apply the Mean Value Theorem in Question 83?
-Van applies the Mean Value Theorem by stating that if a function is continuous and differentiable on a closed interval, then there must exist a value c within that interval where the instantaneous rate of change (the derivative) is equal to the average rate of change over the interval. He uses this theorem to identify the statement that must be true.
What formula does Van use to find the speed of a particle in Question 84?
-Van uses the formula for the speed of a particle in parametric equations, which is the square root of the sum of the squares of the derivatives of the x and y positions with respect to time. He then evaluates this formula at a specific time t to find the speed.
In Question 85, how does Van determine which graph could represent the function f?
-Van determines the graph by considering the effects of concavity and monotonicity on the approximation of the definite integral by trapezoidal and right Riemann sums. He identifies the graph that is concave up and decreasing, which would cause the trapezoidal sum to over-approximate and the right Riemann sum to under-approximate the definite integral.
What is the method Van uses to find the points of inflection in Question 86?
-Van uses the method of finding the second derivative of the function and then graphing it to count the number of sign changes within the given interval. A point of inflection occurs where the second derivative changes sign, indicating a change in concavity of the function's graph.
How does Van solve the Cavalieri's principle problem in Question 89?
-Van solves the problem by considering an individual equilateral triangle cross-section of the solid and calculating its area using the formula for the area of an equilateral triangle. He then integrates this area over the given interval to find the volume of the solid.
What is the concept Van uses to determine the height of the object at the instant it reaches maximum upward velocity in Question 91?
-Van uses the concept of setting the derivative (in this case, the derivative of velocity, which is acceleration) equal to zero to find the instant when the object reaches maximum upward velocity. He then plugs this time back into the original height function to find the height at that instant.
In the final question, how does Van find the value of c for which the instantaneous rate of change equals the average rate of change?
-Van finds the value of c by first calculating the average rate of change of the function over the given interval and then setting the derivative of the function equal to this average rate. He solves for c by finding the intersection of the derivative function and the constant average rate, which represents the value of c that satisfies the condition.
Outlines
📈 Calculating Continuity and Limits - Question 76
This paragraph discusses the analysis of a graph of function 'f' to determine which statement must be false. The statements consider the existence of 'f(a)', the definition of 'f' from 0 to 'a', the continuity of 'f' at 'x=a', and the existence of the limit as 'x' approaches 'a'. The paragraph concludes that the false statement is the existence of the derivative 'f prime' at 'x=a', due to a removable discontinuity at that point.
📚 Taylor Polynomials and Derivatives - Question 77
The paragraph focuses on finding the third derivative of a function 'f' using its fifth-degree Taylor polynomial 'p(x)' centered at 'x=0'. It explains the process of identifying the term associated with the third derivative in the polynomial and using algebra to solve for 'f triple prime of zero', which results in a value of negative 30, corresponding to choice A.
🔄 Related Rates and Circle Properties - Question 78
This section deals with related rates, specifically the rate of increase in the area of a circle whose radius is increasing at a constant rate. Using the given circumference of 20 pi meters, the paragraph derives the rate of increase in the area (da/dt) and calculates it to be 4 pi square meters per second, which matches choice C.
📌 Chain Rule Application - Question 79
The content revolves around applying the chain rule to find 'h prime of 1', where 'h' is a composite function. By substituting values from a given table and performing the necessary calculations, the paragraph concludes that 'h prime of 1' equals 10, which corresponds to choice D.
🌟 Net Change and Integral Calculus - Question 80
This paragraph explores the concept of net change using integral calculus. It involves calculating the total amount of crops destroyed by insects over a period from day 7 to day 14. By integrating the given rate function over the specified interval and rounding to the nearest ton, the paragraph finds the answer to be 125 tons, aligning with choice A.
🏞️ Limits and Sine Functions - Question 81
The paragraph examines the limit of the sine of a function 'f' as 'x' approaches 1, using the graph of 'f'. By analyzing the graph and applying the limit to the function, the sine of two is calculated to be approximately 0.909, which corresponds to choice A.
↗️ Altitude Changes and Integration - Question 82
This section discusses the rate of change of a hot air balloon's altitude and calculates the change in altitude during the time it is decreasing. By finding the times when the rate function 'r of t' is negative and integrating over these intervals, the paragraph identifies the correct limits of integration and matches the answer to choice A.
📉 Mean Value Theorem and Derivatives - Question 83
The paragraph investigates various statements regarding a function 'f' that is continuous and differentiable on a closed interval [0, 4]. Using the Mean Value Theorem, it determines that there must exist a value 'c' in the interval where the derivative of 'f' at 'c' equals the average rate of change of 'f' over the interval, which is choice E.
🚀 Speed Calculations and Parametric Equations - Question 84
The content focuses on calculating the speed of a particle given its parametric equations. By using the formula for speed and plugging in the given values, the paragraph calculates the speed at 't=3' to be approximately 6.884, which corresponds to choice C.
🔢 Definite Integrals and Approximations - Question 85
This paragraph discusses the use of trapezoid and right Riemann sums to approximate definite integrals. It explains the conditions under which these sums over or under approximate the actual integral and identifies a graph that matches the criteria of being concave up and decreasing, which is choice A.
∫ Inflection Points and Derivatives - Question 86
The paragraph deals with finding the number of points of inflection for a function 'f' on a given interval. By taking the second derivative of 'f' and analyzing its sign changes within the interval from -1.8 to 1.8, the paragraph concludes that there are four sign changes, corresponding to choice C.
🚦 Particle Motion and Integral Calculus - Question 87
This section involves calculating the position of a particle moving along the x-axis when its velocity first equals zero. By integrating the velocity function from time zero to the time when velocity is zero and adding the initial position, the paragraph finds the position to be 2.816, which matches choice C.
📊 Average Function Value and Intervals - Question 88
The paragraph examines the average value of a function 'f' on a closed interval [2, 4]. By analyzing the given graphs and using the average function value formula, the paragraph determines that the graph corresponding to choice C has the property that the average value of 'f' on the interval [2, 4] is equal to 1.
🏗️ Cavalieri's Principle and Volume Calculation - Question 89
This section applies Cavalieri's principle to calculate the volume of a solid bounded by the graph of '2x - x^2' with equilateral triangular cross-sections perpendicular to the x-axis. By integrating the area of a single cross-section over the interval [0, 2], the paragraph finds the volume to be 0.462, which corresponds to choice D.
📊 Net Change from Derivative Graph - Question 90
The paragraph explores the concept of net change using the graph of the derivative 'f prime' of a function 'f'. Given that 'f(0) = 0', it analyzes the areas under the graph of 'f prime' to determine the values of 'f' at different points. The paragraph concludes that 'f(3)' is greater than 'f(1)', which corresponds to choice B.
🚀 Maximum Velocity and Height - Question 91
This section calculates the height of an object at the instant it reaches maximum upward velocity. By finding when the derivative of the velocity function equals zero and substituting this time back into the original height function, the paragraph determines the height to be 10.263 at the time of maximum upward velocity, which matches choice B.
🔍 Mean Value Theorem for Functions - Question 92
The paragraph applies the Mean Value Theorem to find the value of 'c' where the instantaneous rate of change of 'f' at 'x=c' is the same as the average rate of change over a given interval. By calculating the average rate of change and solving for when the derivative equals this average, the paragraph finds the value of 'c' to be 2.164, which corresponds to choice C.
Mindmap
Keywords
💡Multiple Choice Questions
💡Graph of a Function
💡Continuity
💡Derivative
💡Taylor Polynomial
💡Related Rates
💡Chain Rule
💡Integral
💡Parametric Equations
💡Mean Value Theorem
💡Cavalieri's Principle
Highlights
The speaker, Van, is reviewing the 2003 AP Calculus BC multiple-choice questions, focusing on the calculator section.
Question 76 discusses the continuity and differentiability of a function, highlighting the importance of understanding these concepts for the AP exam.
In Question 77, Van explains how to find the value of a third derivative using a Taylor polynomial, emphasizing the use of factorials and algebraic manipulation.
For Question 78, Van covers related rates, showing how to find the rate of increase in the area of a circle when the radius is increasing at a constant rate.
Question 79 involves the chain rule, where Van demonstrates how to find the derivative of a composite function and how to use given values from a table to solve for a specific derivative.
Question 80 explores the concept of integrals representing the net change of a function, specifically calculating the total amount of crops destroyed by insects over a given time period.
In Question 81, Van uses a graph to find the limit of a function as x approaches a certain value, showcasing the application of limits in calculus.
Question 82 is a tricky question about the rate of change of a hot air balloon's altitude, where Van explains how to find the exact times when the altitude is decreasing.
For Question 83, Van goes through each statement with the given values of a function to determine which must be true, using the mean value theorem as a justification.
Question 84 involves finding the speed of a particle using parametric equations and the formula for speed, which Van demonstrates how to input into a calculator.
In Question 85, Van discusses the trapezoid and right Riemann sums for approximating definite integrals and how the concavity and monotonicity of a function affect these approximations.
Question 86 requires finding the number of points of inflection on a graph within a given interval, which Van approaches by finding the second derivative and looking for sign changes.
For Question 87, Van applies the concept of integrals to find the position of a particle when its velocity is first equal to zero, using the initial position and the integral of the velocity function.
Question 88 involves finding a graph that represents a function with a specific average value over an interval, which Van solves by considering the properties of linear and non-linear functions.
In Question 89, Van uses Cavalieri's principle to find the volume of a solid with equilateral triangular cross-sections, demonstrating the application of calculus to geometry.
Question 90 focuses on the relationship between the integral of a derivative and the net change in a function's value, which Van uses to evaluate different statements about the function's behavior.
For the final question, Question 91, Van discusses finding the height of an object at the instant it reaches maximum upward velocity by setting the derivative of velocity to zero and solving for time.
Throughout the session, Van emphasizes the importance of knowing and applying various calculus formulas and theorems, as well as the strategic use of a calculator in solving problems.
Transcripts
Browse More Related Video

AP Calculus BC Practice Exam 2012 - Calculator Multiple Choice questions 76-92

AP Calculus AB 2012 Multiple Choice (calculator) - Questions 76 - 92

AP Calculus AB 2008 Multiple Choice (Calculator) - Questions 76-92

AP Calculus AB 2008 Multiple Choice (No Calculator)
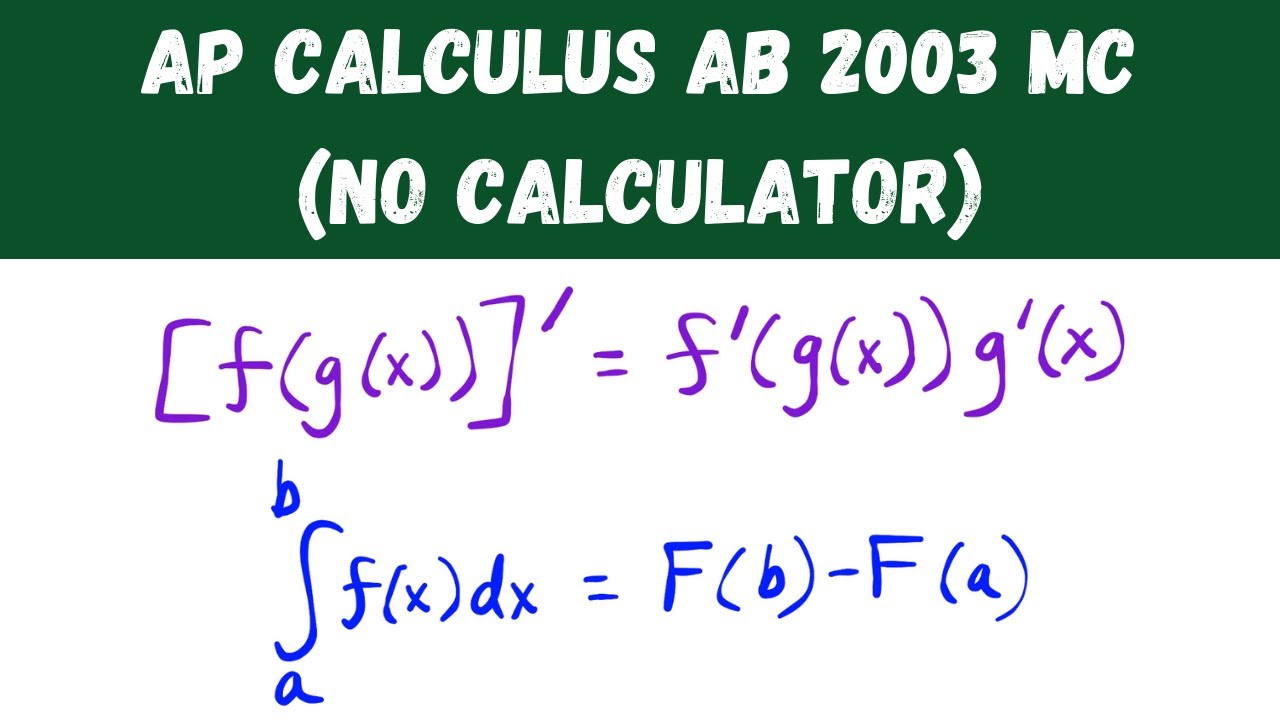
AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28

AP Calculus AB 1998 Multiple Choice No Calculator
5.0 / 5 (0 votes)
Thanks for rating: