AP Calculus AB 1998 Multiple Choice No Calculator
TLDRThe video script is a comprehensive walkthrough of multiple-choice questions from the AP Calculus AB test. The speaker, Vinton, methodically approaches each problem, emphasizing the importance of understanding calculus concepts such as points of inflection, the use of derivatives, and the application of the Fundamental Theorem of Calculus. He also discusses the evaluation of definite integrals, the use of Rolle's Theorem and Mean Value Theorem, and the interpretation of piecewise functions. Vinton provides strategies to avoid common pitfalls, such as misapplying substitution methods or overlooking sign changes in second derivatives. The script is an invaluable resource for students preparing for calculus exams, offering clear explanations and techniques to solve a variety of calculus problems.
Takeaways
- 📚 The first step in finding a point of inflection is to calculate the first and second derivatives of the function, and set the second derivative to zero to find the x-coordinate.
- 🔍 For piecewise functions and definite integrals, consider the signed area under the curve, treating areas under the x-axis as negative and those above as positive.
- 🧮 When integrating, use the power rule and the fundamental theorem of calculus, being cautious of not overcomplicating with unnecessary substitutions like natural logarithms or au sub.
- 📉 For Rolle's Theorem and Mean Value Theorem, remember that if a function is continuous on a closed interval and differentiable on an open interval, the Mean Value Theorem applies, and there will be an absolute minimum and maximum.
- 🚫 Avoid being misled by distractor answer choices, such as adding areas together when they should be considered separately due to their signs.
- 🔑 Memorize theorems for quick recall; for instance, a function that is continuous on a closed interval and differentiable on an open interval will have an average rate of change equal to the instantaneous rate of change at some point within the interval.
- ✅ Always solve for y in functions where possible, as it simplifies the process of finding derivatives and integrals.
- 📈 When given a graph of a function's flow, multiply the rate (per hour) by the time (hours) to find the total amount, as the units will cancel out to give the desired unit of measurement.
- 🤔 For limits, always check both the left and right sides and ensure they are equal; if not, the limit does not exist.
- 📐 To find the equation of a tangent line, use the derivative to find the slope and a given point to determine the equation of the line.
- 🔬 When dealing with second derivatives in factored form, look for sign changes across intervals to determine points of inflection, not just setting the factors to zero.
- 📉 For finding the average value of a function over an interval, use the formula which involves integrating the function over the interval and dividing by the length of the interval.
Q & A
What is the first step to find the x-coordinate of the point of inflection of a graph?
-The first step is to find the first derivative of the given function using the power rule.
Why is it important to look for a sign change in the second derivative when finding the point of inflection?
-A sign change in the second derivative indicates a change in the concavity of the function, which is a characteristic of a point of inflection.
How do you calculate the area under a curve for a piecewise function?
-You calculate the area of each segment of the piecewise function separately, taking into account the sign of the area (positive or negative), and then sum these areas to find the total signed area.
What is the Fundamental Theorem of Calculus Part 1 used for?
-The Fundamental Theorem of Calculus Part 1 is used to find the antiderivative of a function, which is essentially the reverse operation of differentiation.
Under what conditions does Rolle's Theorem apply?
-Rolle's Theorem applies when a function is continuous on a closed interval and differentiable on the corresponding open interval, and the function values at the endpoints of the interval are equal.
How can you determine if a function has an absolute minimum or maximum on a closed interval?
-If a function is continuous on a closed interval, by the Closed Interval Method (or Extreme Value Theorem), the function will have an absolute minimum and absolute maximum on that interval.
What is the key to solving the problem involving the flow of oil through a pipeline?
-The key is to find the area under the curve of the graph, which represents the flow rate over time. Multiplying the flow rate (barrels per hour) by the time (hours) gives the total volume of oil in barrels.
How do you find the instantaneous rate of change of a function at a specific point?
-You find the instantaneous rate of change by taking the derivative of the function and then evaluating it at the specific point of interest.
What is the strategy for finding the value of K that makes the definite integral of an expression equal to zero?
-Assume the 'if' part of the statement is true, and then manipulate the integral expression to find the value of K that would result in the integral being zero over the given interval.
How do you determine the intervals on which a function is increasing?
-Use the derivative test by finding the first derivative of the function, determining its critical points, and then creating a sign chart to identify where the derivative is positive, indicating where the function is increasing.
What is the shortcut for applying the Chain Rule when differentiating a composition of functions?
-Start from the outside function and work your way in, differentiating the outer function first and then multiplying by the derivative of the inner function.
Outlines
📚 AP Calculus AB Test Preparation
The speaker, Vinton, introduces the topic of the video: preparing for the AP Calculus AB test without a calculator. He emphasizes the importance of understanding terms like 'point of inflection' and outlines the process of finding it by taking the first and second derivatives of a given function. Vinton also explains how to approach a question involving a piecewise function and definite integrals, using the concept of signed area under the curve. He warns against common mistakes, such as misapplying the Fundamental Theorem of Calculus and overlooking the importance of sign changes in the second derivative.
🧮 Solving Definite Integrals and Rolle's Theorem
Vinton continues the discussion on calculus by illustrating how to calculate the value of a definite integral using simple shapes like trapezoids. He advises on avoiding unnecessary complexity and emphasizes the power rule for integration. The video also covers Rolle's Theorem and the Mean Value Theorem, highlighting the conditions under which they apply. Vinton demonstrates how to evaluate integrals using these theorems and cautions against incorrect assumptions that could lead to choosing the wrong answer.
📈 Calculus Theorems and Problem-Solving Strategies
The speaker delves into various calculus problems, touching on the application of the Fundamental Theorem of Calculus, part one, and the importance of memorizing calculus theorems. He also discusses the concept of a function being continuous on a closed interval and differentiable on an open interval. Vinton provides a step-by-step approach to solving problems, including finding derivatives and applying the chain rule. He stresses the importance of understanding the context of given information and using it effectively to solve problems.
🚶♂️ Particle Motion and Derivatives
Vinton explores the concept of a particle's motion along the x-axis, focusing on finding the velocity equal to zero by taking the derivative of the position function. He also discusses the application of the Fundamental Theorem of Calculus, part two, to find derivatives of area functions. The video covers the calculation of instantaneous rates of change and the use of the quotient rule for differentiation. It concludes with a problem involving the flow of oil through a pipeline, where the goal is to approximate the total number of barrels of oil.
🔢 Limits, Differentiability, and Chain Rule
The speaker discusses how to find limits of piecewise functions and determine where a function is not differentiable. He explains the concept of a function having a vertical tangent and how to identify points of non-differentiability. Vinton also covers the calculation of derivatives using the chain rule, particularly when dealing with composite functions. He provides a detailed example of finding the derivative of a function involving the sine of an exponential function.
📉 Graph Analysis and Derivative Applications
Vinton focuses on analyzing the graph of a twice-differentiable function to determine the order of function values, derivatives, and second derivatives at a specific point. He explains how to find the equation of a tangent line using derivatives and how to identify points of inflection by examining the second derivative. The video also covers solving for a constant in a differential equation by separating variables and integrating. It concludes with a discussion on determining intervals where a function is increasing using the derivative test.
🏔 Maxima/Minima, Area Calculation, and Intermediate Value Theorem
The speaker discusses finding maximum acceleration on a closed interval using the closed interval method and the concept of concavity. He then moves on to calculating the area between two graphs and applying the Intermediate Value Theorem to determine the number of solutions a function must have. Vinton also covers calculating the average value of a function over an interval using integration and concludes with finding the derivative of a tangent function at a specific point, emphasizing the importance of trigonometric knowledge in calculus.
Mindmap
Keywords
💡Point of Inflection
💡Definite Integral
💡Fundamental Theorem of Calculus Part 1
💡Rolle's Theorem
💡Mean Value Theorem
💡Chain Rule
💡Quotient Rule
💡Product Rule
💡Critical Points
💡Concavity
💡Derivative
Highlights
The importance of having an automatic response to terms like 'point of inflection' which involves finding where the second derivative equals zero.
Using the power rule for derivatives and the concept of sign change in the second derivative to identify points of inflection.
Calculating the area under a curve represented by a piecewise function, emphasizing the treatment of areas above and below the x-axis.
The application of the fundamental theorem of calculus to simplify the process of integration without resorting to complex substitutions.
Memorizing theorems such as Rolle's Theorem and the Mean Value Theorem for their automatic application in calculus problems.
The use of the chain rule in derivatives, especially when dealing with composite functions.
Solving for the exact value of a function at a specific point by plugging in the value into the derived function.
Evaluating the flow of oil through a pipeline by calculating the area under the curve represented by the flow rate over time.
Using the quotient rule for derivatives and the importance of recognizing the structure of the rule for efficient problem-solving.
The concept of differentiability and how to identify points where a function is not differentiable by looking for discontinuities or vertical tangents.
Finding the velocity and position of a particle along the x-axis by taking the derivative of the position function.
Applying the fundamental theorem of calculus part two to find the derivative of an area function, leading to a simplified solution.
Using the chain rule for derivatives of composite functions involving three different functions, such as sine, exponential, and linear functions.
Ordering the values of a function, its first derivative, and its second derivative based on the graph's concavity and slope.
Finding the equation of a tangent line by using the derivative of the function at a given point and the point itself.
Identifying points of inflection by analyzing the sign changes of the second derivative in factored form, avoiding common traps.
Solving for a specific value in an integral expression that makes the definite integral equal to zero, using the properties of the integral's limits.
Solving differential equations by separating variables and integrating both sides, leading to the general solution of the equation.
Determining intervals where a function is increasing using the derivative test and a sign chart, a fundamental technique in calculus.
Using the graph of a function to infer the behavior of its derivative, taking into account the function's concavity and monotonicity.
Applying the closed interval method to find the maximum value of an acceleration function on a given interval.
Calculating the area between two curves by setting up an integral that represents the difference of the functions over a specific range.
Using the intermediate value theorem to determine conditions under which a function must have at least two solutions to an equation.
Calculating the average value of a function over an interval using the integral and the length of the interval.
Finding the derivative of a composite function, such as the tangent function, by applying the chain rule and considering the derivatives of the inner and outer functions.
Transcripts
Browse More Related Video

AP Calculus AB 2008 Multiple Choice (No Calculator)

AP Calculus BC 2003 Multiple Choice (calculator) - Questions 76 - 92

AP Calculus BC Practice Exam 2012 - Calculator Multiple Choice questions 76-92

AP Calculus AB 2008 Multiple Choice (Calculator) - Questions 76-92

AP Calculus AB/BC Multiple Choice Practice Test (2012 AP CED Problems)
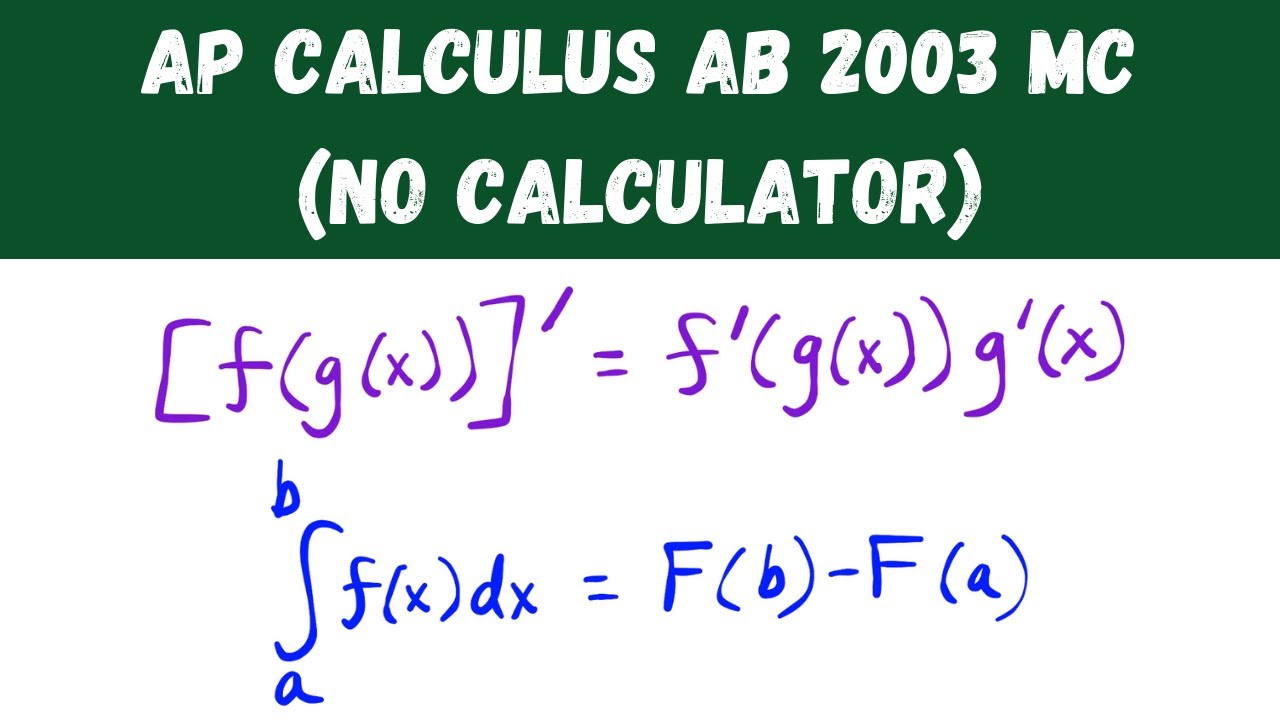
AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28
5.0 / 5 (0 votes)
Thanks for rating: