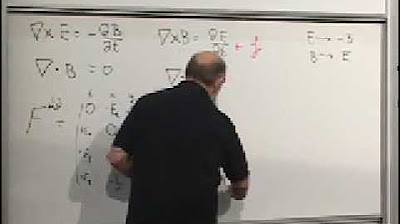Classical Mechanics | Lecture 9
TLDRThe video script is a detailed lecture from Stanford University, focusing on the concepts of angular momentum, gyroscopes, and the formulation of classical mechanics using Poisson brackets. It transitions into the study of electric and magnetic forces, particularly the motion of charged particles in magnetic fields. The lecturer introduces the idea of fields as physical quantities that vary with space and time, using examples like temperature and air pressure to illustrate scalar fields, and wind velocity for vector fields. The script delves into vector calculus, discussing the del operator, divergence, curl, and gradient. It also explores the principle of least action and the Lagrangian formulation for deriving the equations of motion for a particle under the influence of electric and magnetic fields. The importance of the vector potential in describing magnetic fields and the concept of gauge invariance are highlighted. The lecture concludes with the Lorentz force law, which combines electric and magnetic forces, and touches on the implications of special relativity.
Takeaways
- 📚 The lecture begins with a review of angular momentum, gyroscopes, and Poisson brackets in the context of classical mechanics.
- 🌀 The concept of a rotating sphere of charge is introduced as an analogy to a gyroscope, highlighting the relationship between angular momentum and magnetic fields.
- 🔋 Electric forces on charged particles are discussed, emphasizing that these forces are derived from potential energy and are conservative in nature.
- 🧲 Magnetic forces are introduced as a new topic, distinct from electric forces, and are not described by potential energy derivatives.
- 🎓 Vector calculus is briefly introduced as a mathematical tool necessary for understanding fields, which are physical quantities that depend on space and time.
- 📐 The concept of a field is explored, differentiating between scalar fields (like temperature) and vector fields (like wind velocity), with an emphasis on their spatial and temporal variability.
- 🔗 The 'nabla' or 'del' operator is introduced as a key component in vector calculus, used to differentiate fields to create new fields.
- 🔄 The principles of divergence and curl are explained, relating to the spreading and circulating tendencies of fields, respectively.
- ⚖️ The importance of the 'epsilon' or 'levi-cevita' tensor is discussed in the context of cross products and its utility in expressing these operations in three dimensions.
- 🧲 The magnetic field (B) is described as a divergence-free field, meaning it has no sources or sinks, which is a fundamental property derived from experimental evidence.
- 🔵 The vector potential (A) is introduced as a field that can represent the magnetic field through its curl, but it is noted that A is not unique and subject to gauge transformations, which do not affect the physical observables.
Q & A
What was the main topic discussed in the lecture?
-The main topic discussed in the lecture was the study of electrostatic forces, magnetic forces on charged particles, and the mathematical formalism related to the motion of charged particles in fields, including the use of vector calculus and the concept of fields in physics.
What is the significance of Poisson brackets in the context of the lecture?
-Poisson brackets were mentioned as a tool used to reformulate classical mechanics in a new form. They are particularly useful for studying the motion of rigid bodies, although the lecture aimed to move on to the subject of electric and magnetic forces.
How does the lecturer describe the concept of a field in physics?
-A field is described as a physical quantity that depends on space and time. It can be a scalar field, like temperature or air pressure, which has magnitude but no direction, or a vector field, like wind velocity, which has both magnitude and direction.
What is the role of the vector calculus in the study of fields?
-Vector calculus is essential for creating new fields from existing ones through differentiation. It involves the use of the del operator, a 'fake vector' that allows for the manipulation of fields to derive new insights into their behavior.
What is the difference between electric and magnetic forces as discussed in the lecture?
-Electric forces are described by the derivative of a potential energy with respect to position, and they are due to electric fields produced by stationary charged particles. Magnetic forces, on the other hand, are not described by potential energy derivatives and are associated with the motion of charged particles in a magnetic field. These forces are of a different type and are described by a principle of least action, Lagrangian, or Hamiltonian mechanics.
What is the significance of the divergence theorem in the context of electric and magnetic fields?
-The divergence theorem is significant because it states that the divergence of any curl is always zero, which is a fundamental property of magnetic fields. For electric fields, the divergence is related to the charge density, meaning that electric fields spread out from charges. In contrast, magnetic fields have no sources or sinks, as no magnetic monopoles have been found, making their divergence zero.
What is the Lorentz force, and how is it related to the motion of charged particles?
-The Lorentz force is the combined electric and magnetic force experienced by a charged particle. It is given by the electric charge times the electric field (E) plus the electric charge times the velocity (v) cross the magnetic field (B), represented as F = q(E + v × B). This force is crucial for understanding how charged particles move and interact with electromagnetic fields.
What is the principle of least action, and how does it relate to the motion of charged particles?
-The principle of least action is a fundamental principle in physics that states that the path taken by a particle between two points is the one for which the action is minimized. In the context of charged particles, this principle is used to derive the equations of motion that describe how the particles move under the influence of electric and magnetic fields.
What is the role of the vector potential in describing magnetic fields?
-The vector potential (A) is a field that is used to describe magnetic fields. It is related to the magnetic field (B) through the curl of A being equal to B. The vector potential is not unique and can be altered by a gauge transformation without changing the physical magnetic field, making it a useful mathematical tool for describing magnetic fields in terms of the principle of least action.
How does the gauge transformation affect the action in the context of electromagnetism?
-A gauge transformation changes the vector potential by adding a gradient of a scalar function. However, this transformation does not affect the physical quantities derived from the action, such as the equations of motion. The action itself is not gauge-invariant, but the physical predictions, such as the trajectory of a charged particle, are gauge-invariant.
What is the relationship between the Coriolis force and the magnetic force on a charged particle?
-The Coriolis force and the magnetic force on a charged particle share a similar mathematical form, involving the cross product of velocity with another vector. The Coriolis force arises in rotating reference frames and is proportional to the mass of the particle and its velocity, while the magnetic force is proportional to the charge of the particle, its velocity, and the magnetic field.
Outlines
📚 Introduction to Electrodynamics and Vector Calculus
The lecture begins with a review of angular momentum and the Poisson bracket form of classical mechanics. It then transitions into the subject of electric and magnetic forces, emphasizing the need to understand vector calculus for those who are not already familiar with it. Fields are introduced as physical quantities that depend on space and time, with examples including scalar fields like temperature and vector fields like wind velocity.
🧲 Force Fields and the Concept of Locality
The paragraph delves into force fields, such as electric and magnetic fields, which are more fundamental than scalar fields. It discusses the concept of locality, where the effect of a field is local to its immediate neighborhood. The importance of differentiating fields to create new ones is highlighted, introducing the 'nabla' or 'del' operator, an upside-down triangle symbol, as a key component in the calculus of fields.
🔢 The Del Operator and Scalar Fields
The del operator's role in operating on fields to produce other fields is explored. It acts on scalar fields, such as temperature, to produce vectors with components that are derivatives of the scalar field. The paragraph also touches on the construction of scalars from vectors, such as the square of the electric field, and the concept of scalars being invariant regardless of the direction from which they are observed.
🟢 Divergence and Cross Product in Vector Calculus
The concept of divergence, which is a scalar resulting from the dot product of the del operator and a vector, is introduced. The cross product of two vectors is then discussed, with its components defined and a condensed notation using the Levi-Civita symbol is provided. The paragraph explains the properties of the cross product and how it can be represented in a matrix form.
🔍 Exploring the Epsilon Symbol and Anti-symmetry
The epsilon symbol, crucial for the cross product in three dimensions, is defined. It is anti-symmetric, meaning its value changes sign when any two indices are interchanged. The properties of the epsilon symbol are explored, including its values and how it can be used to represent the cross product of vectors in a concise form.
🧲 Magnetic Fields and Their Properties
The paragraph focuses on magnetic fields, which are divergence-free, meaning they have no sources like electric fields do. The concept of magnetic monopoles is introduced as a hypothetical source of magnetic fields, which, if discovered, would require a reevaluation of current theories. The lecture emphasizes that magnetic fields, as currently understood, do not have sources and are represented by the vector B.
🤔 The Vector Potential and Its Non-uniqueness
The vector potential, denoted as A, is introduced as a field that can be written such that the magnetic field B is the curl of A. However, A is not unique; it can be altered by adding the gradient of any scalar field without changing B. This transformation is known as a gauge transformation, and the paragraph discusses the implications of this non-uniqueness on the physical interpretation of A.
🏗️ Constructing the Lagrangian for a Charged Particle in a Magnetic Field
The lecture aims to construct a Lagrangian that, through the principle of least action, will yield the force law for a charged particle in a magnetic field. The electric part of the force is straightforward, being derived from the potential energy. The challenge lies in incorporating the magnetic force into the Lagrangian, which requires the introduction of the vector potential A.
🔄 Gauge Invariance in Electromagnetic Theory
The final paragraph addresses the concern of gauge invariance when constructing the Lagrangian. It is shown that while a gauge transformation changes the action, it does not change the equations of motion derived from the action. This means that the physical solutions obtained from the action principle are gauge invariant, ensuring that the physics remains unchanged despite the mathematical ambiguity in the vector potential A.
Mindmap
Keywords
💡Angular Momentum
💡Poisson Brackets
💡Vector Calculus
💡Fields
💡Nabla Operator
💡Divergence
💡Curl
💡Lorentz Force
💡Gauge Transformation
💡Lagrangian Mechanics
💡Action Principle
Highlights
The lecture revisits angular momentum, gyroscopes, and Poisson brackets in the context of classical mechanics reformulated using these mathematical tools.
A rotating sphere of charge is analogous to a gyroscope in its interaction with magnetic fields, a concept further explored in the provided notes.
The transition to the subject of electrostatic and magnetic forces on charged particles, with a focus on how magnetic fields affect motion in a novel way not previously covered.
Introduction to vector calculus as a fundamental mathematical tool for understanding fields, which are physical quantities that depend on space and time.
Explanation of scalar and vector fields, using examples like temperature (scalar) and wind velocity (vector) to illustrate the concepts.
The concept of 'locality' in fields, where the effect of a field is limited to its immediate neighborhood or where the field is present.
Differentiation of fields using the 'nabla' or 'del' operator, a key component in the calculus of fields that allows for the creation of new fields.
The use of the Levi-Civita symbol (epsilon) in providing a condensed notation for cross products, which is essential in vector calculus.
The theorem stating that the divergence of any curl is always zero, a fundamental result in vector calculus with implications for physical fields.
The magnetic field is defined by its action on charged particles and is characterized by having a divergence that is always equal to zero.
The vector potential 'A' is introduced as a field that can represent the magnetic field through its curl, although it is not unique and subject to gauge transformations.
Gauge transformations, which alter the vector potential without changing the physical magnetic field, are a key concept in understanding the underlying physics.
The Lorentz force law, which describes the combined electric and magnetic forces on a charged particle, is derived from first principles.
The importance of the principle of least action in formulating a Lagrangian that gives rise to the Lorentz force law for charged particles in electromagnetic fields.
The Lagrangian for a particle in a magnetic field includes a term involving the vector potential, which is crucial for deriving the magnetic force component of the Lorentz force.
The gauge invariance of physical laws, such as the motion of charged particles, is maintained despite the non-uniqueness of the vector potential in the Lagrangian.
The action principle is used to derive the equations of motion for a charged particle in an electromagnetic field, showcasing the deep connection between theory and observable phenomena.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: