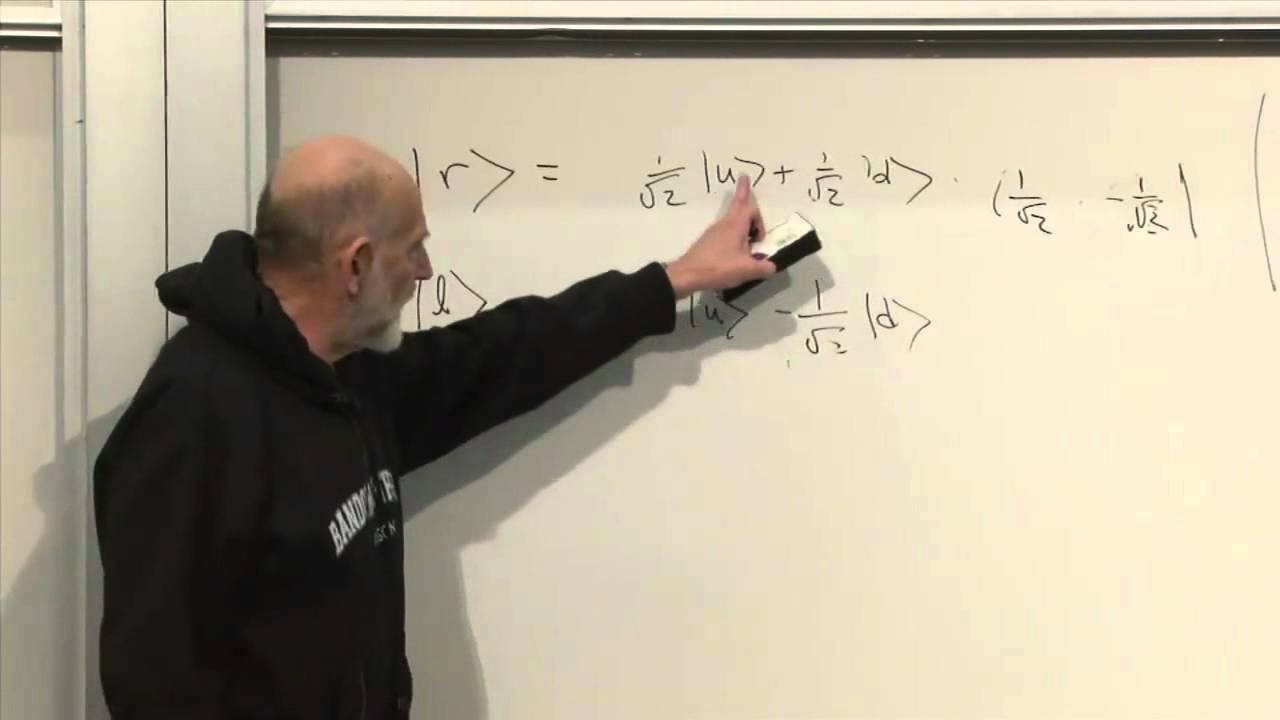Lecture 2 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe video script delves into the foundational concepts of quantum mechanics, contrasting it with classical physics. It introduces the viewer to the idea of a quantum bit or qubit, which unlike a classical bit that has a binary state, exists in a superposition of states. The script explores the abstract concept of a vector space, essential for understanding quantum states, and explains how these states can be represented by complex numbers. It further discusses the role of complex vector spaces in describing the possible configurations of quantum systems. The inner product of vectors is highlighted as a means to calculate probabilities in quantum states, a key aspect of quantum mechanics. The script also touches upon the concept of observables, which are measurable quantities in quantum systems, and sets the stage for further exploration of linear operators and matrices as representations of these observables in future content.
Takeaways
- 🎓 **Quantum Mechanics vs. Classical Physics**: The script introduces the transition from classical physics, which deals with discrete states and classical logic, to quantum mechanics, which operates on a different, probabilistic logic.
- 🚀 **Quantum Bit (Qubit)**: Unlike classical bits that have two states (0 or 1), a qubit can exist in multiple states simultaneously, thanks to the principles of quantum superposition.
- 🧲 **Spin of an Electron**: The electron's spin is likened to a vector with directionality, which can be thought of as a tiny magnet with a north and south pole, despite not being an actual bar magnet.
- 📈 **State Preparation and Measurement**: The process of preparing an electron in a specific spin state and then measuring it involves using magnetic fields and observing the emitted radiation.
- 🤔 **Quantum Weirdness**: The script highlights the 'weirdness' of quantum mechanics, where an electron can be prepared in any direction but upon measurement, only two outcomes are possible: up or down.
- 📊 **Probability Distribution**: The state of a quantum system is not deterministic; instead, it is described by a probability distribution that gives the likelihood of finding the system in a particular state.
- 🔍 **Vector Spaces and Quantum States**: The states of quantum systems, such as an electron, are represented by vectors in a complex vector space, which is a fundamental concept for understanding quantum mechanics.
- 🧮 **Complex Numbers in Quantum Mechanics**: Complex numbers, which include real numbers and imaginary numbers, are essential in the mathematical representation of quantum states and operations.
- 🔗 **Inner Product**: The inner product of two vectors in a complex vector space, found by multiplying corresponding components and summing them, is a key operation in quantum mechanics, related to the probability amplitudes.
- 🌀 **Entanglement**: The script alludes to the concept of entanglement, a quantum phenomenon where particles become interconnected so that the state of one instantly influences the state of another, regardless of distance.
- 🔄 **Unitary Operators**: Unitary operators, which preserve the length of vectors, represent quantum operations that can be performed on a system, such as changing its state without absorbing or amplifying it.
Q & A
What is the basic concept of a quantum bit or qubit?
-A quantum bit or qubit is the fundamental unit of quantum information. Unlike a classical bit that can be in a state of 0 or 1, a qubit can exist in a state of superposition, where it is both 0 and 1 simultaneously, until measured.
What does the term 'state space' refer to in the context of quantum mechanics?
-In quantum mechanics, the 'state space' refers to the set of all possible states a quantum system can be in. It is a mathematical structure that allows for the description of a quantum system's state using vectors.
How does classical logic differ from the logic used in quantum mechanics?
-Classical logic is based on a boolean space where each point represents a state, and the logic is deterministic. Quantum mechanics, however, uses a different kind of logic that allows for probabilities and superpositions, which is non-deterministic and can lead to phenomena like quantum entanglement and wave-particle duality.
What is the role of complex numbers in quantum mechanics?
-Complex numbers are essential in quantum mechanics as they allow for the description of quantum states and operations in a way that real numbers cannot. They are used in the mathematical framework of quantum mechanics to represent the probability amplitudes of quantum states.
What is the significance of the electron's spin in quantum mechanics?
-The electron's spin is a fundamental property that contributes to its intrinsic angular momentum. It is associated with a quantum mechanical magnetic moment, and it can be thought of as a vector that can point in any direction in space, which is crucial for understanding quantum states and their measurement.
How does the concept of a vector space relate to the states of a quantum system?
-A vector space, specifically a complex vector space, is used to represent the states of a quantum system. Each possible state of the system corresponds to a vector in this space, and the rules of vector addition and scalar multiplication correspond to the combination and preparation of quantum states.
What is the meaning of 'normalizing' a quantum state vector?
-Normalizing a quantum state vector means ensuring that the sum of the probabilities of all possible outcomes of a measurement is equal to one. This is done by setting the magnitude of the vector to one, which is equivalent to the condition that the inner product of the vector with itself equals one.
What is the difference between a 'ket' and a 'bra' in quantum mechanics?
-In quantum mechanics, a 'ket' is a symbol used to denote a quantum state as a column vector, while a 'bra' is a row vector and represents the complex conjugate transpose of the ket. Together, they are used to define the inner product of two vectors in a complex vector space.
How does the concept of an 'observable' in quantum mechanics relate to measurable quantities?
-An observable in quantum mechanics is a physical quantity that can be measured. It is represented by a hermitian matrix or operator acting on the state space. The possible results of a measurement are the eigenvalues of the observable, and the probability of obtaining a particular result is given by the squared magnitude of the corresponding eigenvector's coefficient in the state vector.
What is the significance of a hermitian matrix in quantum mechanics?
-A hermitian matrix, which is equal to its own complex conjugate transpose, is significant in quantum mechanics because it represents an observable quantity. The eigenvalues of a hermitian matrix are real, which corresponds to the reality of physical measurements.
How does the process of measurement in quantum mechanics affect the state of a quantum system?
-In quantum mechanics, the process of measurement causes the quantum system to collapse from a superposition of states to a single definite state. The probability of collapsing into a particular state is determined by the squared amplitude of the corresponding component in the system's state vector.
Outlines
📚 Introduction to Quantum Mechanics and Qubits
The video begins with an introduction to quantum mechanics, contrasting it with classical physics. It explains the concept of a quantum bit or qubit, which is fundamentally different from a classical bit. The speaker uses the example of the electron's spin to illustrate the principles of quantum mechanics, highlighting the use of vector spaces and the abstract nature of quantum states as opposed to the discrete states in classical physics.
🧲 Electron Spin and Magnetic Moments
The paragraph delves into the electron's spin, describing it as a vector that can be thought of as a tiny magnet. It explains how electrons can be prepared in a particular spin state using a magnetic field and how they precess around the direction of the magnetic field. The process of detecting the spin state is also covered, involving the emission of radiation as the electron finds its lowest energy state.
🕰 Quantum Measurement and Probabilities
This section discusses the peculiarities of quantum measurement, emphasizing that only two outcomes are possible when measuring the spin of an electron: it either emits a photon (indicating a downward spin) or does not (indicating an upward spin). The speaker highlights the probabilistic nature of quantum mechanics, where the initial preparation of the electron's spin state affects the probabilities of the outcomes upon measurement.
🎢 Quantum Superposition and State Preparation
The speaker explores the concept of superposition in quantum mechanics, where an electron can be prepared in any direction, not just up or down. This is demonstrated by using a magnetic field aligned in different directions. The paragraph also touches on the idea that the outcome of a measurement is probabilistic, with the probability of detecting a photon being dependent on the initial state of the electron.
🧮 Complex Numbers and Vector Spaces in Quantum States
The video introduces the mathematical framework necessary for understanding quantum states, starting with complex numbers and their role in quantum mechanics. It explains the concept of a complex vector space and how it is used to describe the states of quantum systems like electrons. The importance of complex conjugation and the rules for multiplying and adding vectors in this abstract space are also covered.
🔍 Quantum States as Vectors and Inner Products
This part of the video focuses on representing quantum states as vectors in a complex vector space and the significance of inner products. The inner product of a vector with itself is shown to be a real positive number, which can be interpreted as the magnitude or length of the vector. The concept of normalization for quantum states is introduced, which requires the sum of the probabilities (squared magnitudes of the vector components) to equal one.
🔢 Probabilistic Nature of Quantum States
The speaker emphasizes the probabilistic nature of quantum mechanics, where the square of the magnitude of the coefficients in a quantum state vector gives the probabilities of different outcomes upon measurement. The video also touches on the concept of entanglement, suggesting that it will be covered in more depth later, and the importance of repeating experiments to establish probability distributions.
📊 Representing Quantum States with Basis Vectors
The video explains how to represent quantum states using basis vectors, specifically for a quantum bit or qubit. It describes the use of 'plus' and 'minus' kets to represent the states of an electron pointing up or down, respectively. The concept of linear combinations of these basis vectors is introduced to represent arbitrary quantum states, and the importance of the coefficients in these linear combinations is discussed.
🤔 Quantum States and Physical Intuition
The speaker addresses the challenge of visualizing quantum states and the need to 'rewire' our thinking to understand quantum mechanics. They emphasize the importance of grasping the concept of an abstract vector space, which is essential for a complete understanding of quantum mechanics. The video also hints at the connection between these abstract mathematical concepts and physical reality.
🔄 Transformations and Matrices in Quantum Mechanics
The video introduces the concept of linear operators or matrices as transformations in a vector space. It explains how these mathematical constructs can represent physical operations such as stretching or rotating a vector space. The speaker provides examples of different matrices corresponding to different types of transformations, emphasizing that these matrices are central to the mathematical representation of observables in quantum mechanics.
🎰 Observables and Hermitian Matrices
The final part of the video discusses observables in quantum mechanics, which are quantities that can be measured. It introduces the concept of Hermitian matrices, which have the property that their elements are complex conjugates of each other when reflected across the diagonal. The speaker states that Hermitian operators will be postulated as the quantum version of observables in the next session, setting the stage for a deeper exploration of quantum mechanics.
Mindmap
Keywords
💡Quantum Mechanics
💡Qubit
💡Superposition
💡Vector Space
💡Complex Numbers
💡Observables
💡Probability Distribution
💡Entanglement
💡Inner Product
💡Normalization
💡Linear Operator
Highlights
Introduction to quantum mechanics and its departure from classical physics, emphasizing the discrete state space and the use of a new kind of logic.
Explanation of the classical bit as a binary system and contrast it with the quantum bit or qubit, which exists in a superposition of states.
Discussion on the concept of a vector in quantum mechanics, differentiating between spatial vectors and abstract vector spaces.
Illustration of electron spin as a vector that can point in any direction in space, and its analogy to a tiny magnet.
Description of how to prepare a quantum state by using a magnetic field to align the spin of an electron.
The measurement process in quantum mechanics, where an electron in a magnetic field will either emit a photon or not, resulting in two possible outcomes.
The probabilistic nature of quantum mechanics, where the outcome of a measurement is not deterministic but has a probability distribution.
The concept of a complex vector space and its importance in representing the states of quantum systems.
Introduction to complex numbers and their role in quantum mechanics, including the concept of complex conjugate.
Explanation of the inner product of two vectors and its significance in determining the probability distribution of quantum states.
The necessity for quantum states to be normalized, meaning the sum of their probability amplitudes squared equals one.
Differentiation between the quantum bit and classical bit, highlighting the quantum bit's ability to exist in multiple states simultaneously.
Discussion on the abstract nature of quantum mechanics and the need to rewire our thinking to understand it.
Introduction to the concept of observables in quantum mechanics and their connection to hermitian matrices.
Explanation of how the average or expectation value of an observable is calculated in quantum mechanics.
The role of linear operators and matrices in representing transformations of the quantum state space.
Final thoughts on the importance of understanding the mathematical framework of quantum mechanics for grasping concepts like entanglement and superposition.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: