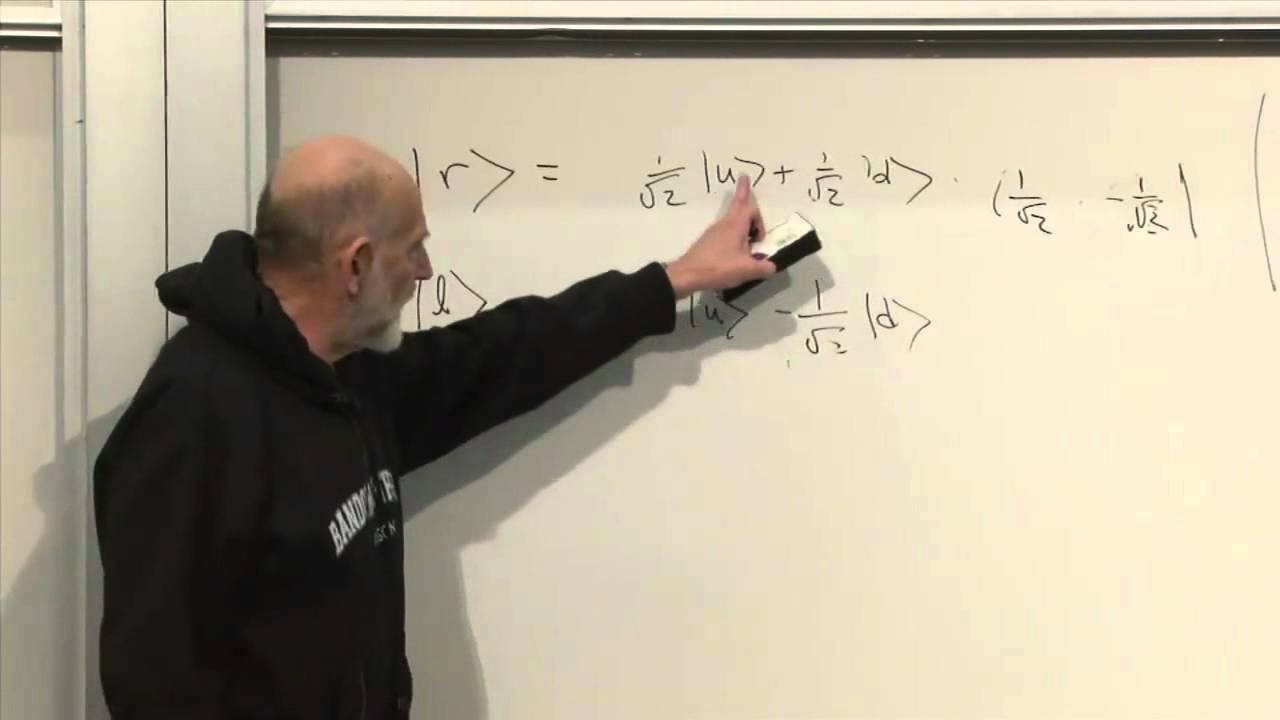Lecture 1 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe video script delves into the foundational concepts of quantum mechanics and its departure from classical physics, emphasizing the limitations of human intuition in grasping these complex theories. It begins with an exploration of how our evolutionary instincts shape our understanding of the physical world, highlighting the remarkable problem-solving abilities of animals. The lecturer then contrasts these innate capabilities with the abstract nature of modern physics, particularly quantum mechanics and relativity, which operate beyond our everyday experiences. The script introduces the idea of information theory in physics, explaining how physical systems can be represented by bits of information. It further discusses the concept of a quantum bit (qubit), contrasting it with classical bits, and the importance of discrete information in quantum mechanics. The lecturer also touches on the mathematical framework of quantum mechanics, including matrices and vectors, which are crucial for understanding the evolution of quantum states. The script concludes with a teaser for the next session, promising a deeper dive into quantum bits and their unique properties.
Takeaways
- 🧠 Our intuitions about the physical world are based on the biological instincts we've inherited through evolution, which are not always compatible with quantum mechanics or relativity.
- 🦁 Animals, like lions chasing antelopes, demonstrate an intuitive understanding of physics concepts such as velocity and direction without formal training.
- 🚀 The development of modern physics required new mathematical frameworks to deal with phenomena outside of human experience, such as near-light velocities.
- ✨ Quantum mechanics and the theory of relativity challenged our intuitive understanding and demanded a conceptual rewiring to grasp abstract concepts like four-dimensional spacetime.
- ⚛️ Quantum mechanics deals with phenomena outside the experience of ordinary humans, such as the behavior of subatomic particles and the uncertainty principle.
- 🔬 The concept of a quantum bit (qubit) is central to quantum mechanics, contrasting with classical bits by offering more nuanced states beyond simply 0 or 1.
- 📊 Information in physics is often represented by numbers, where classical physics typically uses real numbers, and quantum mechanics often uses discrete or binary information.
- 🧩 All physical systems can be represented by a series of bits, which allows for the use of digital computers to simulate and understand physical phenomena.
- 🔍 The level of detail required to track a classical system increases with time, theoretically requiring an infinite number of bits for precise, long-term tracking.
- 🔄 The laws of physics at a fundamental level are deterministic and reversible, meaning that for any given state, there is a unique future and past state.
- 📏 Matrix algebra is a fundamental mathematical tool in quantum mechanics, used to represent the states of a system and the evolution of these states over time.
Q & A
What is the primary challenge when teaching quantum mechanics or relativity?
-The primary challenge is that our intuitive ways of thinking about the physical world, inherited through evolution, are often inadequate for understanding concepts in quantum mechanics and relativity, which operate beyond our everyday experiences.
How do animals demonstrate an intuitive understanding of physics?
-Animals like lions chasing antelopes instinctively understand concepts of velocity and direction, showcasing an innate grasp of physics without formal training.
Why do humans struggle with the concept of velocities approaching the speed of light?
-Humans struggle with this because our intuitions, developed through ordinary experiences, have not encountered such high velocities. The theory of relativity deals with these high-speed scenarios, which are outside the range of human experience.
What is the concept of a 'bit' in the context of information theory?
-A 'bit' is a unit of information that has two possible answers or states, such as yes or no, up or down, or heads or tails. It is the basic unit for representing information in classical and quantum systems.
How does the number of states of a system relate to the number of bits?
-The number of states of a system is 2 to the power of the number of bits. This relationship allows us to quantify the amount of information a system can hold.
What is the space of states in classical physics?
-The space of states in classical physics is an abstract representation of all possible configurations of a system. Each state can be thought of as a point in this space.
Why is the concept of 'unitarity' important in quantum mechanics?
-Unitarity in quantum mechanics ensures that the evolution of a quantum system is reversible, allowing us to reconstruct both the past and future states of the system uniquely.
What is the significance of the inner product of two vectors?
-The inner product of two vectors is a scalar value obtained by multiplying corresponding components of the vectors and summing the results. It's used in various calculations, including determining the cosine of the angle between two vectors.
How does matrix multiplication represent the time evolution of a system?
-Matrix multiplication can be used to update the state of a system over time. By applying a matrix (which represents the rules of evolution) to a vector (which represents the current state of the system), we obtain a new vector representing the system's state after a certain time interval.
Why is it important to understand matrix algebra for quantum mechanics?
-Matrix algebra is fundamental to quantum mechanics because it provides the mathematical framework for describing the states of quantum systems and their evolution over time. It is used to represent quantum states, transformations, and measurements.
What is the role of determinism in classical physics?
-In classical physics, determinism implies that given the current state of a system, its future and past states are uniquely determined by the laws of physics. This principle is crucial for predicting the behavior of physical systems.
How does the concept of reversibility apply to the laws of physics?
-Reversibility means that the laws of physics allow us to trace the state of a system both forward and backward in time. This property is essential for the conservation of information and is a fundamental aspect of many physical processes.
Outlines
😀 Intuition and Evolution in Physics Understanding
The paragraph discusses the intuitive ways humans and animals perceive the physical world, inherited through evolution. It emphasizes that our understanding of physics is often limited by these intuitions, which are not equipped to handle phenomena beyond our ordinary experiences, such as those addressed in quantum mechanics and relativity. The speaker uses examples like a lion chasing an antelope to illustrate how animals instinctively understand complex physics without formal education.
🧐 Quantum Mechanics and the Uncertainty Principle
This paragraph delves into the peculiarities of quantum mechanics, contrasting it with the special theory of relativity. It highlights the difficulty in visualizing quantum phenomena like the motion of an electron or the uncertainty principle, which are outside the range of human experience. The speaker points out that physicists must 'rewire' their intuition to grasp these concepts, which are fundamentally different from classical bits of information.
📊 Classical Bits and Their Representation
The paragraph explains the concept of classical bits, which can be represented by zeros and ones, and how they can describe the state of a physical system. It introduces the notation of using brackets to denote the state of a bit, known as a 'ket.' The speaker also discusses multi-bits, where multiple coins (or bits) are lined up to represent more complex information, and the importance of understanding the number of possible configurations for these bits.
🔢 Counting Possible States in Classical Systems
The focus here is on calculating the number of possible states in classical systems. The paragraph establishes that for a system of 'n' bits, there are 2 to the power of 'n' possible states. It also generalizes this concept to other systems, such as a die, which has six possible outcomes, and introduces the concept of measuring the amount of information in bits, using logarithms to base 2.
🤔 Representing Real Numbers and Physics with Bits
The speaker explores how real numbers and various physical quantities, like temperature, can be approximated and represented in terms of bits. It explains that by using base two representation, any real number can be expressed as a sum or collection of bits, which is crucial for digital computation and simulation of physical systems.
🏗 Discretizing Space and Representing Physics with Bits
This paragraph discusses the representation of physical fields, such as temperature or electric fields, in terms of bits by discretizing space into small cells. It demonstrates that by knowing the state of each cell (e.g., whether it contains a particle or not), one can specify the configuration of a system throughout the space. The speaker also touches on the concept of using bits to represent the motion of particles within this discretized space.
🔄 Laws of Updating and the State Space
The paragraph introduces the concept of 'laws of updating' or 'laws of motion' for systems described by bits. It shows how these laws can be visualized as a series of arrows in a state space, where each arrow represents a transition from one state to another. The speaker also discusses the possibility of having different types of laws, including those that are reversible or irreversible, and the importance of reversibility in physics.
📏 Matrix Algebra and Its Application in Physics
The speaker provides an introduction to matrix algebra, explaining how matrices can be used to represent the time evolution of a system's configuration. It covers the multiplication of matrices by vectors to produce new vectors, and the concept of matrix multiplication to represent multiple updates. The paragraph also touches on the use of row vectors and the importance of matrix algebra in quantum mechanics.
🏋️♂️ Practice with Matrix Algebra for Quantum Mechanics
In this final paragraph, the speaker encourages practice with matrix algebra, emphasizing its fundamental role in quantum mechanics. It mentions the importance of understanding matrix multiplication for both vectors and matrices to grasp the basic mathematics required for quantum mechanics. The speaker also addresses a question about the reversibility of matrices and their inverses, which is crucial for understanding deterministic and reversible laws in physics.
Mindmap
Keywords
💡Quantum Mechanics
💡Relativity
💡Intuition
💡Evolution
💡Velocity
💡Classical Physics
💡Bits
💡Quantum Bit (Qubit)
💡Information Theory
💡Determinism
💡Matrix Algebra
Highlights
The lecturer emphasizes the intuitive limitations humans have when understanding complex physical concepts like quantum mechanics or relativity, which are beyond our evolutionary experiences.
Animals and humans use basic physics concepts, like velocity and force, in their everyday actions, even without formal education in physics.
Modern physics, including quantum mechanics and relativity, deals with phenomena outside the range of human experience, challenging our intuitive understanding.
The theory of relativity and quantum mechanics require new mathematics that is abstract and not easily visualized in four-dimensional SpaceTime.
Physicists 'rewire' their thinking to develop new intuitions for understanding complex parameters in physics.
Quantum mechanics is considered more unintuitive than the special theory of relativity due to the nature of phenomena it deals with.
The讲师 aims to expose the 'weirdness' of quantum mechanics and quantum information, focusing on the basic logic rather than the mathematical formalism.
In classical physics, information is often represented by real numbers, while in quantum mechanics, it is often discrete, such as yes/no or up/down.
A bit of information, which has two possible answers, is a fundamental concept in both classical and quantum information theory.
The number of possible states of a system is 2 to the power of the number of bits, which is a key concept in understanding information content.
The amount of information a system can contain is defined as the logarithm to the base two of the number of states.
Almost any information in physics can be represented in terms of bits, which is why computers can be used to simulate physical problems.
The laws of physics can be thought of as rules for updating the state of a system from one moment to the next.
The space of states can be visualized as a set of points, each representing a possible configuration of a system.
The lecturer discusses the concept of 'unitarity' in quantum mechanics, which relates to the unique evolution of quantum states in time.
The principle of reversibility in physics ensures that the future and past states of a system are uniquely determined from any given state.
The second law of thermodynamics is related to the loss of ability to distinguish different states, not the loss of information itself.
Quantum mechanics allows for the discrete representation of physical systems, eliminating the need for an infinite number of bits to describe a system's state.
The lecturer introduces the concept of matrices and vectors, which are fundamental to the mathematical formulation of quantum mechanics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: