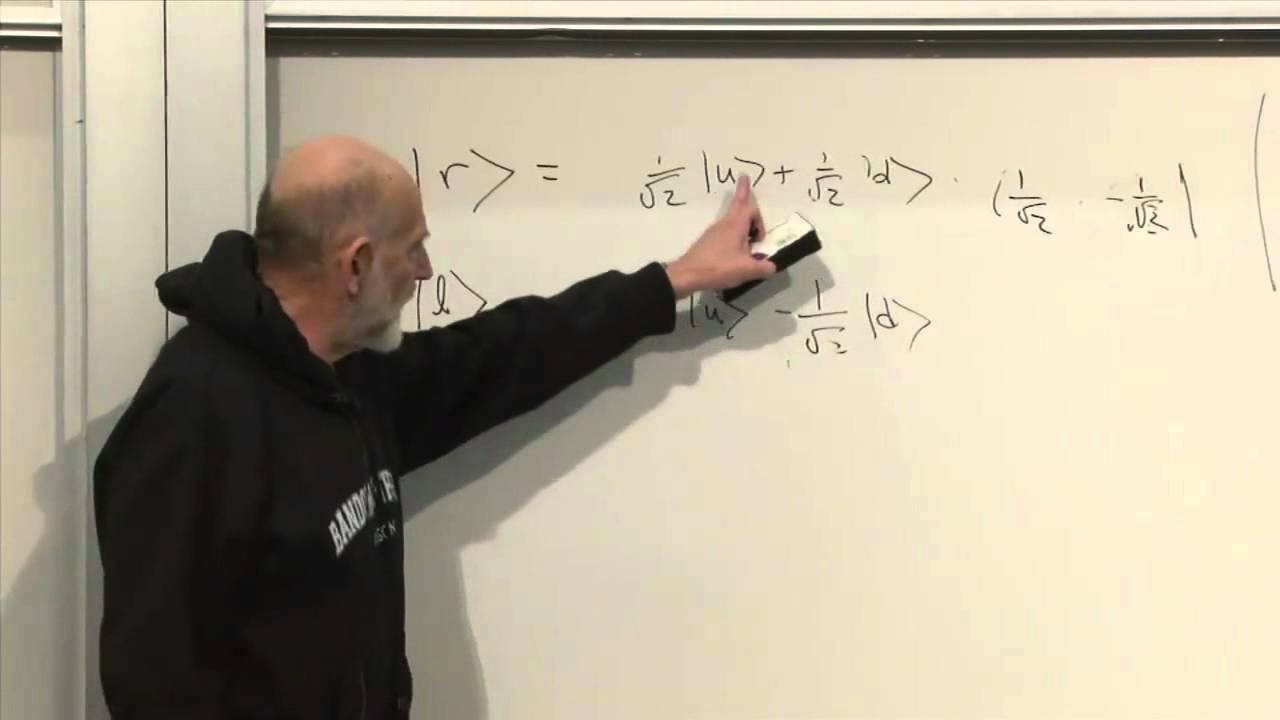Lecture 3 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe video script is an educational lecture on complex numbers and quantum mechanics, delivered by a professor from Stanford University. It begins with an introduction to complex numbers, explaining their real and imaginary parts, and how they can be represented on a two-dimensional surface. The concept of Euler's formula, e^(iΘ), is explored, highlighting its significance in trigonometry and its relation to cosine and sine functions. The lecture then transitions into quantum mechanics, describing it as a framework for calculating probabilities involving different measurements or observables. Quantum states are represented by vectors in a complex vector space, and the importance of normalization is emphasized. The properties of Hermitian matrices are discussed in the context of observables, and the concept of eigenvalues and eigenvectors is introduced, demonstrating that eigenvalues of Hermitian matrices are real. The script delves into the postulates of quantum mechanics, particularly the probabilistic interpretation involving the measurement of quantum states and the role of inner products. The lecture uses the example of electron spin to illustrate these principles, explaining the spin along different axes using the Pauli matrices (σ1, σ2, σ3). The video concludes with an exploration of the anti-commutative property of these matrices and the implications for the measurable values of spin, which can only be plus or minus one. The lecture is rich with mathematical insights and provides a foundational understanding of quantum mechanics.
Takeaways
- 📐 **Complex Numbers**: A complex number has a real part and an imaginary part, which can be represented on a two-dimensional surface with real numbers on the horizontal axis and imaginary numbers on the vertical axis.
- 🧮 **Polar Form**: Complex numbers can also be represented in polar form with a magnitude (R) and an angle (Theta), where R * cos(Theta) gives the real part and R * sin(Theta) gives the imaginary part.
- 🔍 **Exponential Form**: Euler's formula e^(iΘ) = cos(Θ) + i * sin(Θ) is used to represent complex numbers in exponential form, which is particularly useful for calculations involving rotations and oscillations.
- 🌀 **Unitary Numbers**: Numbers of the form e^(iΘ) with X² + Y² = 1 are called unitary numbers and lie on the unit circle. Multiplying a unitary number by its complex conjugate results in one.
- 🚫 **Quantum Mechanics**: Quantum mechanics is a probabilistic calculus for calculating the probabilities of different measurement outcomes, with states represented by vectors in a complex vector space.
- 🌟 **State Vectors**: In quantum mechanics, state vectors are normalized, meaning their length is one, and they represent the state of a quantum system. The probabilities of different outcomes are given by the square of the coefficients in the state vector.
- 🎭 **Observables**: Observables are the measurable quantities in quantum mechanics, represented by Hermitian matrices. The results of measuring an observable are always real numbers.
- 🔢 **Eigenvalues and Eigenvectors**: For a Hermitian matrix, the eigenvalues are real, and the eigenvectors corresponding to distinct eigenvalues are orthogonal. The eigenvalues represent the possible outcomes of measuring the observable.
- 🤝 **Inner Product Space**: The inner product of two vectors in a complex vector space is a complex number, and it is used to calculate the probability amplitudes in quantum mechanics.
- 🤔 **Complex Conjugate**: The complex conjugate of a complex number is essential in quantum mechanics, as it ensures the probability (the square of the absolute value of the amplitude) is real and non-negative.
- 🧲 **Spin Components**: In quantum mechanics, particularly with particles like electrons, the spin components along any axis can only take on values of +1 or -1, reflecting the quantized nature of these properties.
Q & A
What is a complex number and how is it represented on a two-dimensional surface?
-A complex number has a real part and an imaginary part. It can be plotted on a two-dimensional surface where the horizontal axis represents the real part of the number and the vertical axis represents the imaginary part. A point on this plane represents the complex number in the form of 'X Plus i, y', where X is the real part and y is the imaginary part.
What is the polar form representation of a complex number and how is it related to trigonometry?
-The polar form of a complex number is represented in terms of a distance 'R' and an angle 'Theta'. Using elementary trigonometry, the real part 'X' is 'R times the cosine of Theta', and the imaginary part 'Y' is 'R times the sine of Theta'. This form is also expressed as 'Z equals R times e to the i, Theta', where e to the i, Theta is 'cosine Theta plus i, sine Theta'.
Why are complex numbers used in quantum mechanics?
-Complex numbers are used in quantum mechanics due to their mathematical properties that are linked with time evolution and reversibility. They allow for the description of quantum states and observables in a way that real numbers alone cannot capture, particularly when dealing with the probabilistic nature of quantum measurements.
What is the significance of eigenvalues and eigenvectors in the context of Hermitian operators?
-Eigenvalues and eigenvectors of Hermitian operators are significant because they represent the possible measurable values (eigenvalues) of an observable and the states (eigenvectors) in which these values are obtained with certainty. The eigenvalues of a Hermitian matrix are always real, and the corresponding eigenvectors are orthogonal if they correspond to different eigenvalues.
How does the concept of complex conjugation relate to the probability interpretation in quantum mechanics?
-In quantum mechanics, the probability of measuring a particular eigenvalue when the system is in a certain state is given by the square of the absolute value of the inner product of the eigenvector corresponding to that eigenvalue with the state vector. This inner product involves complex conjugation, as the inner product is taken with the complex conjugate of the state vector.
What is the postulate of quantum mechanics that deals with the measurement of quantum states?
-The postulate of quantum mechanics that deals with measurement states that when a quantum system, which is in a state represented by a vector 'B', is measured with respect to an observable 'M' with eigenvalue 'Lambda', the probability of obtaining the result 'Lambda' is given by the square of the absolute value of the inner product of 'B' with the eigenvector corresponding to 'Lambda'.
What are the properties of the Pauli spin matrices Sigma 1, Sigma 2, and Sigma 3?
-The Pauli spin matrices Sigma 1, Sigma 2, and Sigma 3 are Hermitian matrices that represent the observable quantities of the components of the electron spin along the x, y, and z axes, respectively. They share the property that their eigenvalues are +1 and -1, and their squares equal the identity matrix. They also have the property of anticommutativity, meaning that the product of two different Pauli matrices in reverse order is the negative of the original product.
How does the concept of a unit vector relate to the measurement of spin components in an arbitrary direction?
-A unit vector with components (n1, n2, n3) can be used to define a direction in space along which the component of the spin can be measured. The operator corresponding to the spin component along this direction is given by the dot product of the Pauli matrices with the components of the unit vector, resulting in an operator that can be used to predict the outcomes of spin measurements in that direction.
What is the meaning of the inner product of two vectors in quantum mechanics?
-In quantum mechanics, the inner product of two vectors, also known as the dot product, is a complex number that provides information about the angle between the two vectors. Specifically, it is used to calculate the probability of obtaining a particular outcome when measuring an observable in a quantum system.
Why are the results of quantum measurements always real numbers?
-The results of quantum measurements are always real numbers because observables, which are represented by Hermitian operators, yield real eigenvalues. This is a requirement for physical measurements, as they must correspond to real, measurable quantities.
What is the significance of the square of the Pauli matrices being the identity matrix?
-The fact that the square of each Pauli matrix is the identity matrix signifies that the possible outcomes of measuring the spin component along any axis are always +1 or -1, regardless of the axis. This is a fundamental aspect of quantum mechanics, reflecting the quantized nature of spin measurements.
How does the concept of orthogonality relate to distinguishable quantum states?
-In quantum mechanics, orthogonality between two states implies that they are distinguishable. If two states are orthogonal, there exists a measurement that can uniquely determine which state the system is in. Conversely, if two states are not orthogonal, they cannot be uniquely distinguished by any measurement.
Outlines
🔢 Introduction to Complex Numbers and Trigonometry
The paragraph begins with an introduction to complex numbers, explaining their real and imaginary parts and how they can be plotted on a two-dimensional surface. It then delves into the representation of complex numbers using distance 'R' and angle 'Theta', and connects this to the properties of exponentials, specifically e^(iTheta). The explanation includes a review of how the multiplication of complex numbers represented as exponentials follows the rules of trigonometry, such as the cosine of the sum of two angles. The paragraph emphasizes the importance of understanding these mathematical concepts as foundational to grasping more advanced topics.
🌀 Unitary Numbers and Quantum Mechanics Postulates
This section discusses unitary numbers, which are complex numbers that lie on the unit circle and have the property that when multiplied by their complex conjugate, the result is one. It then transitions into the basic postulates of quantum mechanics, framing it as a method for calculating probabilities. The paragraph explains that quantum states are represented by vectors in a complex vector space and that the probabilities of different outcomes are determined by these vectors' coefficients. It also touches on the concept of observables, which are the measurable quantities in quantum mechanics.
📈 Normalization and Probability in Quantum States
The paragraph focuses on the normalization of state vectors in quantum mechanics, which ensures that the total probability of all possible outcomes sums up to one. It explains that the coefficients of the state vectors (Alpha and Beta) must satisfy certain conditions to ensure this normalization. The text also explores the concept of observables further, describing how they are represented by matrices or operators and how their measurement results in real numbers. The paragraph concludes by discussing the role of complex numbers in representing probabilities in quantum states and the significance of the phase angle and modulus in a complex number.
🧮 Hermitian Matrices and Observables in Quantum Mechanics
The text introduces Hermitian matrices, which are matrices that are equal to their own conjugate transpose. It explains the properties of these matrices and how they relate to observables in quantum mechanics. The paragraph also discusses the concept of transpose and Hermitian conjugate, leading to the definition of a Hermitian matrix. It emphasizes that the results of measurements (observables) are always real numbers and that observables are represented by Hermitian operators. The properties of these operators are then related back to the probabilities of measuring certain outcomes in a quantum system.
📚 Eigenvalues and Eigenvectors of Hermitian Operators
This paragraph delves into the concept of eigenvalues and eigenvectors, particularly in relation to Hermitian operators. It explains that Hermitian operators always have real eigenvalues and that if a matrix has two different eigenvalues, the corresponding eigenvectors are orthogonal. The text also discusses the significance of eigenvalues as the possible results of measurements for a given observable and how eigenvectors represent states where these eigenvalues can be measured with certainty. The paragraph concludes with an example of finding eigenvalues and eigenvectors for a diagonal matrix.
🎲 Probability Interpretation in Quantum Mechanics
The paragraph discusses the probability interpretation in quantum mechanics. It explains that if a system is prepared in a certain state and an observable with a specific eigenvalue is measured, the probability of obtaining that eigenvalue is given by the square of the inner product between the eigenvector associated with that eigenvalue and the state in which the system was prepared. The text emphasizes that this probability is always a real positive number and less than or equal to one. It concludes with an example calculation of the probability of measuring a specific component of electron spin, given the system was prepared in a state corresponding to a different component.
🧲 Electron Spin and Components in Arbitrary Directions
The final paragraph explores the concept of electron spin and its components along arbitrary directions. It describes how to calculate the component of spin along a given direction using the dot product of the spin operator with a unit vector in that direction. The text also discusses the properties of the spin operator in quantum mechanics, highlighting that the square of the spin component along any direction results in the identity matrix, indicating that the eigenvalues of the spin component are always plus or minus one. This reflects the probabilistic nature of quantum mechanics, where the outcomes of measurements are uncertain until observed.
Mindmap
Keywords
💡Complex Numbers
💡Eigenvalues and Eigenvectors
💡Hermitian Matrices
💡Quantum States
💡Unitary Numbers
💡Spin
💡Probability Interpretation
💡Observables
💡Inner Product
💡Schrodinger's Cat
💡Quantum Entanglement
Highlights
Complex numbers consist of a real part and an imaginary part, plotted on a two-dimensional surface with the real part on the horizontal axis and the imaginary part on the vertical axis.
A complex number can be represented in terms of a distance (R) and an angle (Theta), derived from elementary trigonometry.
The formula e^(i*Theta) = cos(Theta) + i*sin(Theta) is fundamental in representing complex numbers and satisfies the rules of exponentials.
When multiplying exponentials, the exponents are added, which is demonstrated when multiplying e^(i*Theta) by e^(i*Phi), resulting in a real and imaginary part that follows trigonometric identities.
The complex conjugate of a number is obtained by changing the sign of the imaginary part, and when multiplied by the original number, results in a real number.
Numbers of the form e^(i*Theta) that satisfy the equation x^2 + y^2 = 1 lie on the unit circle and are termed unitary numbers.
Every complex number can be expressed as a unitary number multiplied by a real positive number, which is the radius or distance to that point on the complex plane.
Quantum mechanics is a calculus for calculating probabilities, with observables being the measurable quantities that result in real numbers.
State vectors in quantum mechanics are normalized, ensuring the total probability adds up to one, and are represented in a complex vector space.
The probabilities of different outcomes in quantum mechanics are not enough to completely determine the state, as multiplying by a pure phase does not change the magnitude.
Hermitian matrices, which are equal to their own Hermitian conjugate, are used to represent observables in quantum mechanics and have real expectation values.
Eigenvalues of a Hermitian matrix are real, which is significant as they represent the possible measurable values of the observable.
Eigenvectors corresponding to distinct eigenvalues of a Hermitian matrix are orthogonal, a key theorem in quantum mechanics signifying distinguishable states.
The Pauli spin matrices (Sigma 1, Sigma 2, Sigma 3) are Hermitian and have eigenvalues of +1 and -1, representing the possible outcomes when measuring spin components.
The component of spin along an arbitrary direction is given by the dot product of the Pauli matrices with the unit vector in that direction.
The square of the sigma matrices (Sigma 1, Sigma 2, Sigma 3) equals the identity matrix, indicating that the possible measurable values of spin along any axis are +1 or -1.
The anticommutation property of the sigma matrices is crucial, as it ensures that the probabilities of measurement outcomes reflect the quantum state of the system.
The program concludes with a discussion on the probabilities of spin measurements in different directions, emphasizing the probabilistic nature of quantum mechanics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: