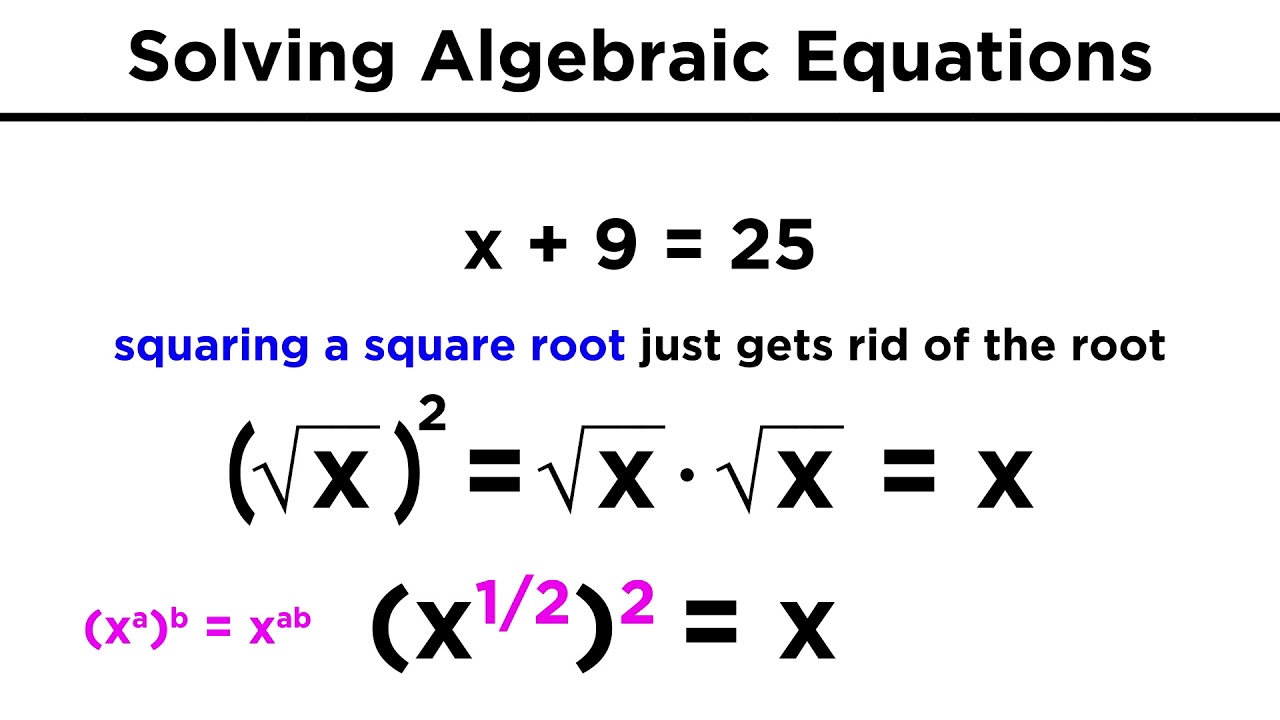The Maths Prof: Changing Subject of Formula EXAM QUESTIONS
TLDRThe video script from 'Math 12' is an educational guide on the process of changing the subject of a formula, a crucial skill in mathematics and science. The presenter walks viewers through several examples, emphasizing the importance of rearranging equations to isolate the variable of interest. Key steps include performing operations in reverse (such as subtracting to counteract addition) and applying these operations consistently to both sides of the equation. The script details the methodical approach of working from the outside inwards to eliminate terms and isolate the variable. It also covers the concept of opposite operations, like squaring to remove a square root or multiplying by the denominator to eliminate fractions. The examples provided range from basic algebraic manipulations to more complex scenarios involving square roots and fractions, offering a comprehensive understanding of the subject.
Takeaways
- 📚 The video is an educational resource discussing the concept of changing the subject of a formula, which is a common practice in math and science.
- 🔍 To isolate a variable, perform operations on both sides of the equation that are opposite to those present, working from the outside inwards.
- ➕ The opposite of addition is subtraction, which is used to eliminate terms away from the variable you're isolating.
- 🟢 When dealing with squared terms, the opposite operation is to take the square root of both sides of the equation.
- 🛑 It's important to apply the same operations to both sides of the equation to maintain equality.
- 📉 To remove a multiplication by a fraction, the opposite is to multiply by the reciprocal, effectively dividing by the fraction.
- 🔢 For a variable within a fraction's denominator, multiply both sides by the denominator to eliminate the fraction.
- 🔗 When a term is subtracted, the opposite is to add, which helps in isolating the variable.
- 📌 Memorizing the opposite operations (addition vs. subtraction, multiplication vs. division, squaring vs. square rooting) is crucial for solving equations.
- 📐 The process of changing the subject involves moving other terms away from the variable until it stands alone on one side of the equation.
- 📝 It's recommended to practice by writing down the steps and checking answers at the end of each example to reinforce understanding.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is changing the subject of a formula, which is an important concept used in math and science.
Why is it necessary to work from the outside inwards when rearranging a formula?
-Working from the outside inwards helps to systematically isolate the variable of interest (the subject) on one side of the equation, by performing operations that cancel out the terms that are not the subject.
What is the opposite operation of adding in the context of rearranging a formula?
-The opposite operation of adding is subtracting. This is used to eliminate terms from the side of the equation where the subject variable is being isolated.
How do you deal with a square root when trying to isolate a variable?
-To deal with a square root, you perform the opposite operation, which is squaring both sides of the equation. This cancels out the square root, bringing the variable closer to being isolated.
What is the process for eliminating a multiplication by a fraction in an equation?
-To eliminate a multiplication by a fraction, you perform the opposite operation, which is multiplying by the reciprocal of the fraction. This effectively cancels out the fraction.
How do you handle a variable within a fraction in the denominator when isolating the subject?
-To handle a variable within a fraction in the denominator, you multiply both sides of the equation by the denominator. This eliminates the fraction and allows you to isolate the variable.
What is the purpose of checking the answer against the original equation?
-Checking the answer against the original equation ensures that the operations performed to isolate the subject were correct and that the final form of the equation is accurate.
Why is it important to perform the same operation on both sides of the equation when rearranging?
-Performing the same operation on both sides of the equation maintains the equality and ensures that the mathematical properties of the equation are preserved throughout the rearrangement process.
What is the role of brackets in an equation when you have multiple terms being multiplied by a number?
-Brackets are used to group terms together, indicating that the multiplication applies to every term within the brackets. This clarity helps avoid confusion and ensures the correct application of the operation.
How does the process of making a variable the subject of a formula help in solving mathematical problems?
-Making a variable the subject of a formula allows you to express the relationship between variables in a way that isolates the variable of interest, which is essential for solving for specific values or understanding the underlying relationship in mathematical and scientific contexts.
What is the significance of the order of operations when rearranging formulas?
-The order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), dictates the sequence in which you perform operations. This ensures that the mathematical expressions are evaluated correctly when rearranging formulas.
Outlines
📚 Understanding Changing the Subject of a Formula
The first paragraph introduces the topic of changing the subject of a formula, a concept crucial for mathematics and science. The speaker encourages viewers to participate actively by taking notes and solving the example questions provided. The explanation begins with an equation where 'x' is the subject to be isolated. The process involves performing operations on both sides of the equation to isolate 'x', such as subtracting six from both sides, taking the square root of both sides to eliminate the squaring operation, and finally adding four to both sides to isolate 'x'. The paragraph emphasizes the importance of working from the outside inwards and performing the opposite operation to isolate the variable.
🔍 Making 'a' the Subject of a Formula
The second paragraph focuses on rearranging a formula to make 'a' the subject. The process involves moving all terms away from 'a' to isolate it. This includes subtracting 'uT' from both sides of the equation, multiplying by 2 to counteract the division by half, and dividing by 'T^2' to remove the multiplication by 'T^2'. The paragraph also covers a specific example where values are substituted into the formula to calculate 'B', and then the formula is rearranged to make 'P' the subject, involving multiplying by 3 and dividing by 'a'.
🧮 Isolating 'X' in a Complex Equation
The final paragraph deals with making 'X' the subject of a formula that includes a square root and a fraction. The process starts by squaring both sides to eliminate the square root, subtracting 8 from both sides to remove the constant, and then multiplying every term by 'X' to eliminate the fraction in the denominator. The opposite operation, which is dividing by the terms inside the brackets, is performed to isolate 'X'. The paragraph concludes with the final rearranged formula where 'X' is isolated on one side.
Mindmap
Keywords
💡Subject of a formula
💡Rearranging equations
💡Opposite operations
💡Working from the outside inwards
💡Square root
💡Substitution
💡Fractions
💡Division
💡Multiplication
💡Simplifying equations
💡Algebra
Highlights
Changing the subject of a formula is an important skill used frequently in math and science
To change the subject, work from the outside inwards to isolate the variable
Use opposite operations to eliminate terms away from the variable (e.g. subtract for add, divide for multiply)
Perform the same operation on both sides of the equation to maintain equality
Example: To solve for x, subtract 6 from both sides to eliminate +6 term
Next, take the square root of both sides to eliminate the square term
Finally, add 4 to both sides to isolate x
In another example, to solve for a, subtract y/T from both sides
Then multiply both sides by 2 to eliminate the 1/2 term
Finally, divide by T^2 to isolate a
To make b the subject, square both sides to eliminate the square root
Then subtract a^2 from both sides to eliminate the a^2 term
Finally, take the square root of both sides to solve for b
In a word problem, substitute given values into the equation to solve for one variable
To make p the subject, multiply both sides by 3 to eliminate the 1/3 term
Then divide by a to isolate p
To make x the subject with a square root and fraction, square both sides first
Then subtract 8 from both sides to eliminate the +8 term
Finally, multiply both sides by the denominator x to clear the fraction, then divide by (y^2-8) to isolate x
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: