AP Calculus AB: Lesson 7.6: Volume using Known Cross Sections
TLDRIn this instructional video, Michele Chromel teaches the method of calculating the volume of solids with known cross-sectional shapes. She illustrates the process using various scenarios, including parabolic, square, equilateral triangular, isosceles right triangular, and semi-circular cross-sections. The lesson emphasizes the importance of understanding the geometry of the problem and setting up integrals to find the volume, with demonstrations of how to visualize and calculate these solids using online interactive tools.
Takeaways
- 📚 The lesson focuses on calculating the volume of solids with known cross-sectional shapes using integral calculus.
- 🔍 Cross-sections perpendicular to the x-axis are considered, with the volume of each slice calculated as the area of the cross-section multiplied by the thickness (Δx).
- 📐 The area function, represented as \( a(x_k) \), is used to denote the area of the cross-section at a specific x-value.
- 🌟 The definite integral is applied to sum up the volumes of multiple slices, set up as \( \int_{a}^{b} a(x) \, dx \).
- 📈 An example is provided where the base of a solid is enclosed by the graphs of \( y = x \) and \( y = x^2 \), with cross-sections having an area given by \( \sin(\frac{\pi}{2}x) \).
- 🛠 The process of finding the volume involves identifying the interval for integration and setting up the integral with the area function.
- 📉 The use of u-substitution is demonstrated for integrating functions like \( \sin(\frac{\pi}{2}x) \) to simplify the calculation.
- 📊 Interactive demonstrations are recommended for visualizing the 3D solids and understanding the cross-sectional shapes.
- 📏 The importance of understanding the shape and size of cross-sections is emphasized for setting up the correct integral.
- 📐 The volume calculation changes based on the shape of the cross-section, such as squares, equilateral triangles, isosceles right triangles, and semicircles.
- 🧩 The script provides a step-by-step approach to set up and solve integrals for different cross-sectional shapes, including handling multiple functions defining the base of the solid.
Q & A
What is the primary topic of the lesson presented by Michele Chromel?
-The primary topic of the lesson is how to find the volume of a solid with cross sections of a known shape.
How does the volume of a slice in a three-dimensional solid relate to its cross-sectional area and thickness?
-The volume of a slice in a three-dimensional solid is the product of the cross-sectional area and the thickness of the slice, represented as the area function 'a of X sub k' times the thickness 'Delta X'.
What mathematical concept is used to sum up the volumes of multiple slices in a solid?
-The mathematical concept used to sum up the volumes of multiple slices is the definite integral.
In the context of the lesson, how is the volume of a solid with a base in the first quadrant and cross sections of a specific area function calculated?
-The volume is calculated using the definite integral of the area function from 'x equals a' to 'x equals b', which in this case is the sine of PI over 2 times X.
What substitution method is suggested for integrating the area function of sine of PI over 2 X?
-The substitution method suggested is u-substitution, where u equals PI over 2 X, and the differential 'du' is the PI over 2 times 'dx'.
How does the intersection point of the functions y=x^2 and y=2x help in determining the interval for integration?
-The intersection point of the functions y=x^2 and y=2x, which occurs at x=2, helps in determining the upper limit of the interval for integration, with the lower limit being the origin (0,0).
What is the significance of the interactive demonstrations provided in the lesson?
-The interactive demonstrations are significant as they help visualize the three-dimensional solid figures from different angles and perspectives, aiding in the understanding of the volume calculation process.
How does the shape of the cross-sections affect the calculation of the volume of the solid?
-The shape of the cross-sections determines the area function used in the integral for calculating the volume. Different shapes, such as squares, equilateral triangles, isosceles right triangles, and semicircles, have different area functions.
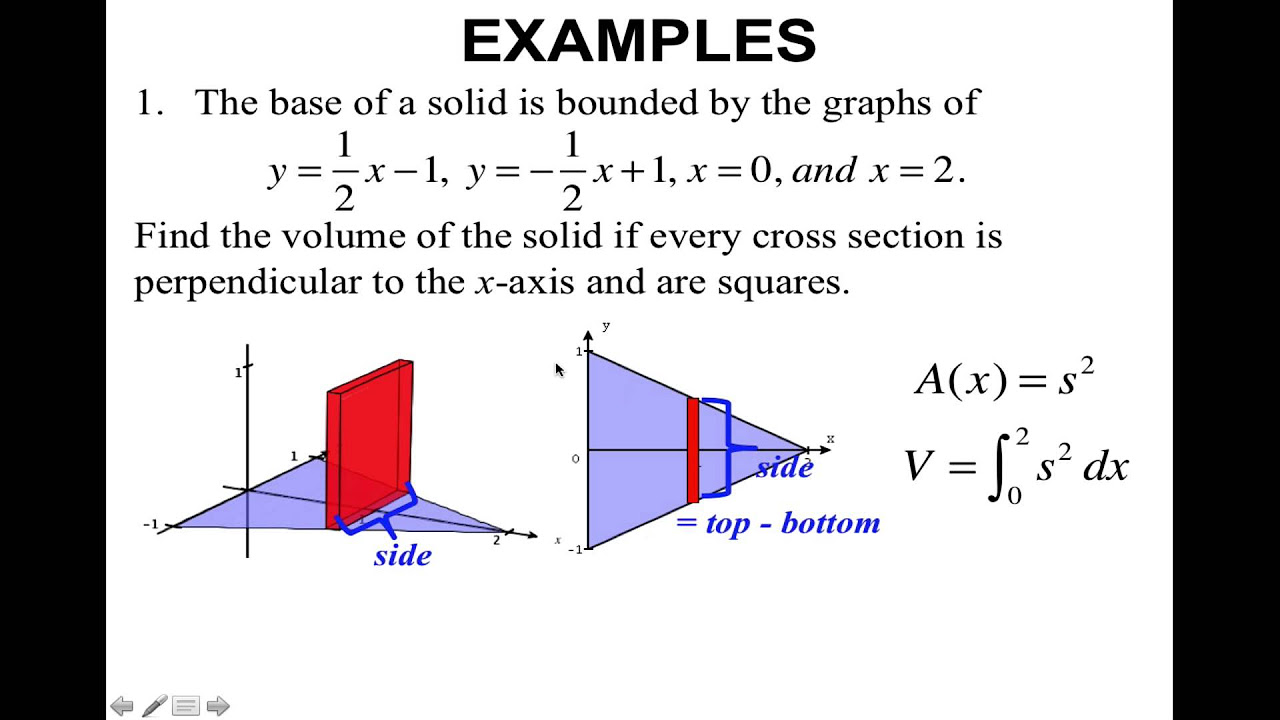
What is the process for setting up the integral to find the volume of a solid with cross-sections perpendicular to the x-axis being squares?
-The process involves squaring the function representing the vertical distance between the two functions defining the base of the solid, multiplying by 'dx', and integrating over the interval defined by the points of intersection of the functions.
In the case of equilateral triangles as cross-sections, how is the area function derived in terms of the side length 's'?
-The area function for an equilateral triangle is derived as the square root of 3 over 4 times 's' squared, where 's' is the side length of the triangle, which is the vertical distance between the two functions defining the base.
How does the presence of two functions defining the base of the solid affect the setup of the integral for volume calculation?
-When two functions define the base of the solid, the area function for the cross-sections is the square of the difference between the two functions, and the integral is set up over the interval between their points of intersection.
What is the key to solving the volume calculation for a solid with quarter circles as cross-sections?
-The key is to identify the radius of the quarter circles as the vertical distance between the functions defining the base, and then use the area function PI over 4 times the square of the radius, integrated over the interval between the points of intersection.
Outlines
📚 Introduction to Calculating Solid Volumes
Michele Chromel introduces the concept of finding the volume of a solid with known cross-sectional shapes. The lesson begins with a scenario involving a 3D solid and parabolic cross-sections perpendicular to the x-axis, each with a thickness represented by Δx. The volume of a single slice is calculated as the area of the cross-section (a(x_k)) times the thickness. The process involves summing these volumes over multiple slices using a definite integral from x=a to x=b, where the area function a(x) is given. An example is provided with a region R enclosed by y=√x, y=x^2, and the x-axis, with cross-sections having an area given by sin(π/2 * x). The integral set-up for the volume calculation is demonstrated.
📐 U-Substitution in Volume Calculations
The script explains the use of u-substitution in integrals to calculate the volume of a solid. The example involves integrating the sine function with respect to u, where u = π/2 * x, and the bounds of integration are adjusted accordingly. The integral of -cos(u) from 0 to π is computed, resulting in a volume calculation that simplifies to 4/π. Interactive demonstrations are recommended for visualizing 3D solids, with three different websites provided for exploring cross-sections of various shapes.
📏 Visualizing Solids with Different Cross-Sections
The video script describes how to visualize 3D solids with different cross-sectional shapes such as squares, equilateral triangles, and semicircles. It explains the process of adjusting sliders to change the number of cross-sections (N value) and the interval end (x value) to better understand the solid's volume. The base of the solid is represented by a region between two functions, and the cross-sections' side lengths are determined by the vertical distance between these functions. The script also demonstrates how to change the shape of the cross-sections from squares to triangles to semicircles using checkboxes.
📐 Setting Up Integrals for Solid Volumes
The script details the process of setting up integrals for calculating the volume of solids with various cross-sectional shapes. It explains how to find the area of a cross-section, such as a square or an equilateral triangle, and how to multiply this area by the thickness (dx) to find the volume of a single slice. The integral of this volume expression over the interval of interest is then used to find the total volume of the solid. The process is illustrated with examples of solids with bases defined by different functions and cross-sections of squares and equilateral triangles.
📘 Calculating Volumes with Isosceles Right Triangles and Semicircles
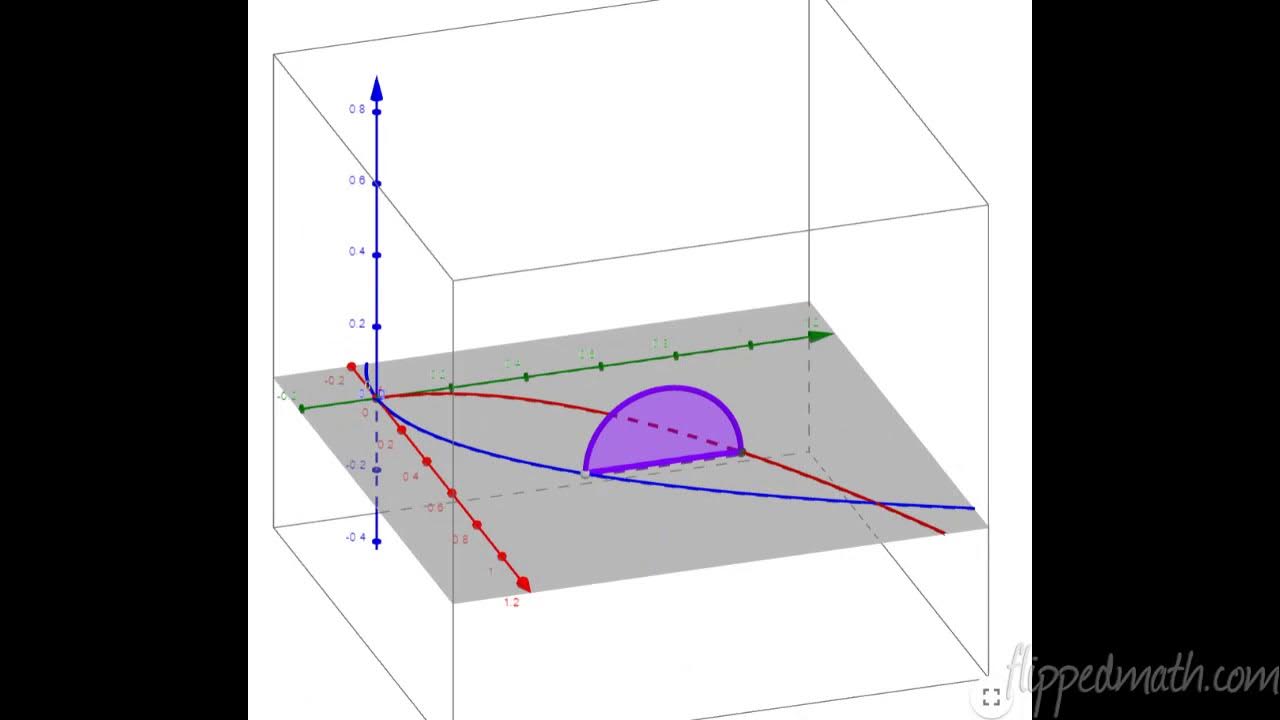
The script continues with the calculation of solid volumes where the cross-sections are isosceles right triangles and semicircles. For isosceles right triangles, the area function is derived from the properties of a 45-45-90 triangle, and the volume is found by integrating the area function over the interval. For semicircles, the area function is one-fourth of the area of a full circle, and the volume is calculated similarly. The process involves identifying the correct area function for the cross-section and integrating it over the specified interval.
🔍 Complex Solids with Multiple Functions Defining the Base
The script addresses more complex scenarios where two functions define the base of the region, and the cross-sections are squares or equilateral triangles. It demonstrates finding the points of intersection between the functions and setting up the integral for the volume of the solid. The process includes squaring the difference of the functions to find the area of the cross-sections and integrating this area over the interval to find the volume. The calculations are shown for both square and equilateral triangle cross-sections.
📊 Final Examples with Quarter Circle Cross-Sections
The final part of the script presents an example where the cross-sections are quarter circles, defined by two functions. The area function for a quarter circle is derived, and the volume of the solid is calculated by integrating this area function over the interval from x=-1 to x=2. The script concludes with the integral calculation and the final volume expressed in terms of π, resulting in a value of 81π/40 after simplification.
🤔 Critical Thinking on Volume Calculations
The script concludes with a prompt for critical thinking about the process of finding the volume of solids with known cross-sections, emphasizing the importance of understanding the process over memorizing formulas. It encourages reflection on the steps taken throughout the lesson for setting up integrals and calculating volumes.
Mindmap
Keywords
💡Volume
💡Cross Sections
💡Definite Integral
💡Area Function
💡Parabolic Shape
💡U-Substitution
💡Sine Function
💡3D Visualization
💡Equilateral Triangle
💡Isosceles Right Triangle
💡Semicircle
Highlights
Introduction to finding the volume of a solid with cross sections of known shapes using calculus.
Explanation of the volume of a slice as the product of the area of the cross section and its thickness (Delta X).
Use of definite integrals to calculate the total volume of a solid by summing up the volumes of multiple slices.
Demonstration of how to set up an integral for the volume of a solid with parabolic cross sections.
Application of the area function to represent the area of cross sections at different x-values.
Example problem involving a solid with a base defined by the intersection of y=x and y=x^2, and cross sections with an area given by sine(π/2 * x).
Graphical representation and intersection points of functions to establish the interval for integration.
Technique of u-substitution for integrating the area function of cross sections.
Final calculation of the volume using the antiderivative of the sine function and adjusting the bounds of integration.
Interactive demonstrations to visualize 3D solids with different cross-sectional shapes.
Exploration of the effect of cross-sectional shape on the volume calculation, including squares, equilateral triangles, and semicircles.
Calculation of the volume of a solid with a base between two functions and cross sections as equilateral triangles.
Use of the Pythagorean theorem to find the height of equilateral triangles for volume calculation.
Setting up integrals for solids with isosceles right triangle cross sections and their volume calculation.
Introduction of semicircle cross sections and the process to find their area for volume integration.
Complex problem-solving involving two functions defining the base and different cross-sectional shapes.
Method to find the volume of a solid with cross sections as quarter circles and its integral setup.
Critical thinking on the general process of finding the volume of solids with known cross sections without memorizing formulas.
Transcripts
Browse More Related Video

Volume Using Known Cross Sections (Slicing) | Calculus 2 Lesson 5 - JK Math

Volume of Solids with Known Cross Sections

Calculus AB/BC – 8.7 Volumes with Cross Sections: Squares and Rectangles
Topic 43-Volumes of Solids with Known Cross Sections
Calculus AB/BC – 8.8 Volumes with Cross Sections: Triangles and Semicircles

Calculating volume by known cross sections
5.0 / 5 (0 votes)
Thanks for rating: