AP Calculus AB 2008 Multiple Choice (No Calculator)
TLDRThis comprehensive video script delves into a variety of AP Calculus AB multiple-choice questions, meticulously guiding viewers through the problem-solving process. The speaker, Vincent, adeptly tackles complex concepts such as limits, derivatives, and integrals, emphasizing the importance of understanding leading terms for limits at infinity, the application of power and chain rules, and the use of L'Hôpital's rule for indeterminate forms. He also explores the continuity and differentiability of functions, employing strategies like u-substitution and the fundamental theorem of calculus. Vincent further investigates the behavior of piecewise functions, the evaluation of functions and their derivatives at specific points, and the application of implicit differentiation. The script concludes with a discussion on the slope of tangent lines, the modeling of real-world phenomena through differential equations, and the approximation of function values using tangent lines. This detailed walkthrough is an invaluable resource for students seeking to enhance their calculus skills and understanding.
Takeaways
- 📚 The first question involves finding the limit as X approaches infinity by considering the leading terms of a rational function, resulting in the answer being negative 2 (Choice B).
- 🔍 For the second question, it's important to not mistake the expression for a natural logarithm and instead apply the power rule, leading to the correct answer of Choice D.
- 📈 Question 3 requires the use of the product rule for differentiation, followed by simplifying the expression by factoring out the greatest common factor, which aligns with Choice D.
- 🔧 In Question 4, a shortcut for integrating functions of the form sine or cosine of a simple expression like 2x is to divide by the derivative of the inside function, which results in Choice B.
- 📉 For limits that result in 0/0, Question 5 demonstrates the application of L'Hôpital's rule, which after multiple applications, leads to the answer Choice A.
- 🧩 In evaluating piecewise functions, as in Question 6, factoring and canceling common factors are essential, leading to the conclusion that only one statement is true (Choice A).
- 🚀 Question 7 deals with finding the position of a particle at a specific time by integrating the velocity function, which is a direct application of the fundamental theorem of calculus, resulting in Choice B.
- 📐 The derivative of a function at a specific point, as in Question 8, can be found using the chain rule, and plugging in the given value yields Choice E.
- 🔽 To find the maximum value of an integral over an interval, as in Question 9, one can use the sign changes of the derivative to determine the absolute maximum, which is Choice D.
- 🔠 When identifying the least value of a function represented in various ways, as in Question 10, it's important to compare methods such as Riemann sums and the actual area under the curve, leading to the correct answer of Choice C.
- 🔄 For determining the behavior of a derivative, as in Question 11, it's crucial to understand where the function is increasing or decreasing, which helps in selecting the correct graph that represents the derivative, which is Choice B.
Q & A
How does one evaluate the limit as X approaches infinity for a rational function?
-To evaluate the limit as X approaches infinity for a rational function, one should consider the leading terms of the numerator and denominator. Since the exponents of the highest terms match, the limit is determined by the ratio of the coefficients of these terms.
What is the correct approach to differentiate the integral of a function with respect to x?
-The correct approach is to use the chain rule, rewriting the integral as the integral of the derivative of the function with respect to x, multiplied by the derivative of the integration variable (in this case, x).
How can one quickly find the antiderivative of sine or cosine of a simple function like 2x?
-Instead of using u-substitution, one can quickly find the antiderivative by dividing by the derivative of the inside function. For sine 2x, it would be -1/2 cosine 2x, and for cosine 2x, it would be 1/2 sine 2x, with appropriate constants added.
What is the application of L'Hôpital's rule when evaluating limits?
-L'Hôpital's rule is applied when evaluating limits that result in an indeterminate form, such as 0/0 or ∞/∞. It involves taking the derivative of the numerator and the denominator and then reevaluating the limit.
How can one determine if a function is continuous at a given point?
-A function is continuous at a given point if the limit as x approaches that point exists and is equal to the function's value at that point. If the function's value at the point does not match the limit, the function is not continuous at that point.
What is the strategy for finding the position of a particle at a given time, given its velocity function?
-The strategy is to integrate the velocity function over the time interval from the initial time to the given time. The integral of the velocity function gives the position function, and applying the fundamental theorem of calculus can help find the position at the desired time.
How does one determine the points of inflection for a function defined by an integral?
-To determine the points of inflection, one should first take the derivative of the function, which is equivalent to the integrand due to the fundamental theorem of calculus. Then, look for sign changes in the second derivative, which indicate points of inflection.
What is the relationship between the rate of spread of a rumor and the number of people who have heard it and those who have not?
-The rate of spread of a rumor is proportional to the product of the number of people who have heard the rumor and the number of people who have not. This relationship can be modeled using a differential equation where the rate of change of the number of people who have heard the rumor is proportional to the current number of people who have heard it times the number of people yet to hear it.
How does one solve a separable differential equation with an initial condition?
-To solve a separable differential equation with an initial condition, one should separate the variables and integrate both sides. Then, apply the initial condition to find the constant of integration and solve for the function.
What is the key to determining the differentiability of a piecewise function at a specific point?
-The key to determining the differentiability of a piecewise function at a specific point is to ensure that the left and right derivatives at that point are equal. If the function is differentiable at the point, it must also be continuous, and the limit from the left and right must exist and be equal at that point.
How can one find the slope of the tangent line to a function at a specific point?
-To find the slope of the tangent line to a function at a specific point, one needs to calculate the derivative of the function at that point. The derivative represents the slope of the tangent line at the given point.
Outlines
📚 AP Calculus AB Multiple Choice Questions Overview
Vincent introduces the video by stating its purpose: to analyze multiple-choice questions from AP Calculus AB, specifically those that require no calculator. He emphasizes the importance of focusing on leading terms when dealing with limits as X approaches infinity in rational functions.
🔍 Evaluating Limits at Infinity and Applying Power Rule
The video delves into solving the first question about evaluating a limit at infinity. Vincent demonstrates how to simplify the expression by considering the leading terms of the numerator and denominator, resulting in the answer being negative 2. He also cautions against incorrectly applying the natural log rule and shows the correct application of the power rule for another question.
📝 Using Product Rule and Simplifying Derivatives
Vincent moves on to question 3, which involves applying the product rule to find the derivative of a given function. He shows the step-by-step process of differentiating and then simplifying the expression by factoring out the greatest common factor, leading to the correct answer choice.
🧮 U-Substitution and Antiderivatives in Integration
For question 4, Vincent discusses the use of u-substitution and the shortcut method for integrating functions of the form sine or cosine of a simple expression like 2x. He outlines the process of dividing by the derivative of the inside function and applying the antiderivative of the trigonometric function.
🔢 L'Hôpital's Rule and Evaluating Piecewise Functions
In question 5, Vincent addresses an indeterminate form and applies l'Hôpital's rule twice to find the limit. For question 6, he evaluates a piecewise function, emphasizing the importance of factoring to find the limit and determining the continuity and differentiability of the function.
🚀 Particle Motion and Velocity Function Integration
Vincent discusses the motion of a particle along an x-axis in question 7, using the given velocity function to find the position of the particle at a specific time. He employs the fundamental theorem of calculus to set up the integral and solve for the position function.
🔄 Derivatives, Chain Rule, and Sine Functions
For question 8, Vincent calculates the derivative of a function involving sine and uses the chain rule. He emphasizes the importance of not getting tripped up by the sine function and to simplify the expression correctly to find the answer.
📉 Evaluating Definite Integrals and Function Maxima
In question 9, Vincent evaluates definite integrals and uses the fundamental theorem of calculus to find the maximum value of a function. He discusses the concept of critical values and how they relate to local and absolute maxima.
📈 Least Value of a Function and Riemann Sums
Vincent examines the graph of a function in question 10 to determine the least value. He compares the area under the curve with various Riemann sums and the trapezoidal sum to find the correct answer.
🔳 Behavior of Derivatives and Points of Inflection
For question 11, Vincent describes the behavior of a derivative based on the graph of a function. He explains how to identify where a function is increasing or decreasing and how to find the points of inflection.
🧵 Chain Rule and Derivatives of Composite Functions
Vincent uses the chain rule to find the derivative of a function in question 12. He emphasizes the importance of being comfortable with the chain rule and simplifies the derivative correctly.
🏞️ Polynomial Functions and Second Derivatives
In question 14, Vincent examines a polynomial function with given second derivative values. He discusses which statements must be true based on the behavior of the first and second derivatives of the function.
🧮 U-Substitution in Integration and Implicit Differentiation
Vincent applies u-substitution in question 15 to solve an integral and uses implicit differentiation in question 16 to find the derivative of an equation involving sine and cosine.
🏡 Points of Inflection in Area Functions
For question 17, Vincent finds the points of inflection in the graph of an area function. He uses the fundamental theorem of calculus and the concept of sign changes in the second derivative.
📐 Tangent Lines and Derivatives in Geometry
In question 18, Vincent finds the value of K for a line tangent to a curve. He uses the derivative of the curve to find the slope of the tangent line and then solves for K.
🏁 Horizontal Asymptotes and Points of Inflection
Vincent finds the horizontal asymptotes of a function in question 19 and the points of inflection in question 20 using the limits as X approaches infinity and the sign changes in the second derivative.
🚦 Velocity and Acceleration in Particle Motion
For question 22, Vincent determines the intervals where the velocity of a particle is increasing by analyzing the concavity of the position function graph and using the concept of acceleration.
📈 Modeling Rumor Spread with Differential Equations
Vincent models the spread of a rumor among a population in question 22 using a differential equation. He sets up the equation based on the rate of spread being proportional to the product of the number of people who have and have not heard the rumor.
🧵 Solving Separable Differential Equations
Vincent solves a separable differential equation in question 23 using initial conditions. He separates the variables, integrates both sides, and applies the initial condition to find the specific solution.
🔍 Analyzing Differentiability and Tangent Lines
For question 25, Vincent determines the value of C plus D for a piecewise function that is differentiable at a specific point. He uses the concept of continuity and differentiability to find the values of C and D.
🔑 Derivative of an Inverse Function
In the final question, Vincent finds the derivative of the inverse function G at a given point. He uses the formula for the derivative of an inverse function and the given values of F and its derivative to find the answer.
Mindmap
Keywords
💡Limit
💡Leading Term
💡Natural Log
💡Product Rule
💡Chain Rule
💡Antiderivatives
💡L'Hôpital's Rule
💡Piecewise Function
💡Velocity and Position
💡Derivatives
💡Differential Equations
Highlights
Approaching AP Calculus AB multiple choice questions without a calculator involves focusing on the leading terms of the numerator and denominator for limits as X goes to infinity.
To evaluate limits at infinity, compare coefficients of the highest terms as the exponents usually match.
Rewriting expressions using power rules can help avoid mistaking them for natural logarithms.
The product rule is essential for finding derivatives, especially when not multiplying terms out to save time.
Factoring out the greatest common factor can simplify derivatives and match them to the correct answer choices.
Using substitution and dividing by the derivative of the inner function can simplify integrals of trigonometric functions.
L'Hôpital's rule is applied when plugging in values results in an indeterminate form like 0/0.
For piecewise functions, limits can be found by factoring and canceling common factors, then plugging in the value.
The continuity and differentiability of a function at a point can be assessed by comparing function values and limits.
The position of a particle can be determined from its velocity function using the fundamental theorem of calculus.
The derivative of a function at a specific point can be found using the chain rule and plugging in the value.
To find the maximum value of an integral over an interval, consider the sign changes of the derivative of the function.
The least value among different summation methods for a function can be determined by comparing the areas under the curve.
Identifying the correct graph for the derivative of a function involves analyzing the function's increasing and decreasing intervals.
The derivative of an exponential function can be found using the chain rule and simplifying the expression.
The composition of functions and the chain rule are used to find the derivative of a function composed with another function.
Given selected values of a second derivative, one can deduce true statements about the behavior of the function using the intermediate value theorem.
U-substitution is a technique used in integration, where a new variable u is set equal to a function of x, and the integral is rewritten in terms of du.
Implicit differentiation is used when dealing with functions of two variables, x and y, which are not explicitly separated.
A function's points of inflection can be found by analyzing the sign changes of its second derivative.
The slope of the tangent line to a curve at a specific point is equal to the derivative of the function at that point.
Horizontal asymptotes of a rational function can be found by analyzing the behavior of the function as X approaches infinity or negative infinity.
The x-coordinates of a point of inflection on a graph can be determined by checking the sign changes of the second derivative.
The velocity of a particle is increasing where the acceleration, or the second derivative of position, is positive.
A differential equation can model the spread of a rumor through a population, with the rate of spread proportional to the product of the number of people who have heard the rumor and have not heard it.
Solving a separable differential equation involves separating variables, integrating both sides, and using initial conditions to find the constant of integration.
The approximation of a function value using a tangent line involves plugging the point into the equation of the tangent line derived from the function's derivative at a given point.
The differentiability of a piecewise function at a point is determined by ensuring the left and right derivatives at that point are equal.
The slope of the line tangent to an inverse trigonometric function can be found using the chain rule and plugging in the value for x.
Identifying the correct differential equation for a given slope field involves checking which equation results in a derivative of zero for specific values of x and y.
The derivative of the inverse function of a differentiable function can be found using the formula that involves the reciprocal of the derivative of the original function.
Transcripts
Browse More Related Video

AP Calculus BC 2003 Multiple Choice (calculator) - Questions 76 - 92

AP Calculus AB 1998 Multiple Choice No Calculator
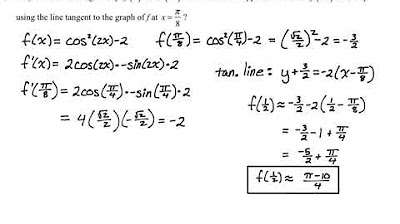
AP Calc AB & BC Practice MC Review Problems #4
AP Calculus AB Review
AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28

2021 Live Review 3 | AP Calculus AB | How to Find Limits & Continuity
5.0 / 5 (0 votes)
Thanks for rating: