AP Calc AB & BC Practice MC Review Problems #4
TLDRThe video script offers a comprehensive review of AP Calculus AB and BC multiple-choice problems, focusing on a variety of calculus concepts. The presenter begins by addressing a problem involving the velocity of a particle moving along the x-axis, using trigonometric functions and derivatives to find the first instance of zero velocity. The discussion then shifts to applying the second fundamental theorem of calculus to find derivatives of integrals, and using tangent lines to approximate function values. The video continues with an exploration of limits, including the use of L'Hôpital's rule for indeterminate forms and the application of the intermediate value theorem. The script concludes with a problem involving the analysis of a twice differentiable function, emphasizing the importance of understanding the behavior of functions and their derivatives. Throughout the video, the presenter highlights the necessity of mastering algebraic techniques and trigonometric identities to successfully tackle calculus problems.
Takeaways
- 📚 Start by attempting the AP Calculus AB and BC review problems before watching the video to check your understanding and compare your solutions.
- 🔍 For the first question, the velocity of a particle moving along the x-axis is calculated using the derivative, which is the product of the exponential function and trigonometric functions.
- 🧮 Use the product rule and chain rule to find derivatives, as demonstrated in the video, to solve for the velocity of the particle and other calculus problems.
- 📈 Understand the second fundamental theorem of calculus to find derivatives of integrals, as shown in the example with the function f(x) involving secant squared.
- 📐 Learn to approximate function values using tangent lines, which requires knowledge of derivatives and the point-slope form of a line.
- 🤔 For multiple-choice questions involving functions with absolute values, be familiar with the graph of the absolute value function to identify discontinuities and other properties.
- 📉 Recognize that the limit definition of a derivative can be used to find the slope of a tangent line or to determine the derivative at a specific point.
- 🧷 Use completing the square and long division as algebraic techniques when dealing with integrals, especially when the degree of the numerator is equal to or greater than the denominator.
- 📌 Memorize the unit circle and the values of sine, cosine, and tangent for the '17 famous angles' to solve trigonometric equations efficiently.
- 🔑 L'Hôpital's rule is a useful method for finding limits of indeterminate forms like 0/0 or ∞/∞, and it should be applied until a non-indeterminate form is reached.
- 🔍 For problems involving tables of function values, use the information provided to make informed assumptions about the function's behavior, such as the presence of critical points or the sign of the derivative.
Q & A
What is the first time T at which the velocity of the particle is zero, given the position function X(T) = cos(2t) / e^(2t)?
-The first time T at which the velocity is zero is when T = 3π/8. This is determined by setting the derivative of the position function to zero and solving for T, which involves using trigonometric identities and the properties of exponential functions.
How can you find the derivative of an integral using the second fundamental theorem of calculus?
-The second fundamental theorem of calculus states that the derivative of an integral from a constant to a variable x of some function f(t) is simply f(x). That is, if F(x) = ∫[a, x] f(t) dt, then F'(x) = f(x).
What is the expression for f'(x) if f(x) = cos²(2x) - 2?
-The derivative f'(x) is found using the chain rule. For f(x) = cos²(2x) - 2, the derivative is f'(x) = 2 * cos(2x) * (-sin(2x)) * 2, which simplifies to -4 * sin(2x) * cos(2x).
How do you approximate a function value using a tangent line at a given point?
-To approximate a function value using a tangent line, you first find the slope of the tangent line, which is the derivative of the function at the point of tangency. Then, use the point-slope form of a line to write the equation of the tangent line. Finally, plug in the x-value for which you want to approximate the function value.
What is the limit as X approaches 4 of (f(X) - f(4)) / (X - 4) for the function f(X) = ln(3X - 2)?
-This limit is asking for the derivative of the function f at the point x = 4. By applying the definition of the derivative, the limit as X approaches 4 of (f(X) - f(4)) / (X - 4) is f'(4), which is 3/(3*4 - 2) = 3/10.
How do you integrate the function 1 / (x² + 6x + 13) dx?
-The integration of 1 / (x² + 6x + 13) dx can be approached by completing the square in the denominator to transform it into a form suitable for an arctangent integral. After completing the square, the integral becomes ∫(1 / (1 + (x + 3)²/4)) dx, which simplifies to (1/2) * ∫(1 / (1 + (x + 3)²)) dx, and this can be integrated as (1/2) * arctan((x + 3)/2) + C.
What algebraic techniques are useful for integrating when there's a quadratic in the denominator?
-When integrating a function with a quadratic in the denominator, completing the square and long division are two algebraic techniques that can be particularly useful. Completing the square helps to transform the quadratic into a perfect square trinomial, while long division is used when the numerator's degree is equal to or greater than the denominator's degree.
What is the approximation for f(3.2) using the tangent line to the graph of f at the point (3, 4) if f(x) = (3x - 1)^(2/3)?
-To approximate f(3.2) using the tangent line, first find the derivative f'(x) of the function f(x). Then, calculate the slope of the tangent line at the point (3, 4) and use the point-slope form to find the equation of the tangent line. Finally, substitute x = 3.2 into the tangent line equation to get the approximation.
How do you evaluate the limit as x approaches 0 of (e^(3x - 3x) - 1) / (5x²)?
-The direct substitution of x = 0 into the expression results in an indeterminate form of 0/0. To evaluate this limit, apply L'Hôpital's rule, which involves taking the derivative of the numerator and the denominator separately and then re-evaluating the limit.
What is the derivative with respect to X of the integral from (-√3) to X of arctan(t)² dt?
-According to the second fundamental theorem of calculus, the derivative with respect to X of the integral from a to X of some function g(t) dt is simply g(X). Therefore, the derivative of the integral from (-√3) to X of arctan(t)² dt with respect to X is arctan(X)².
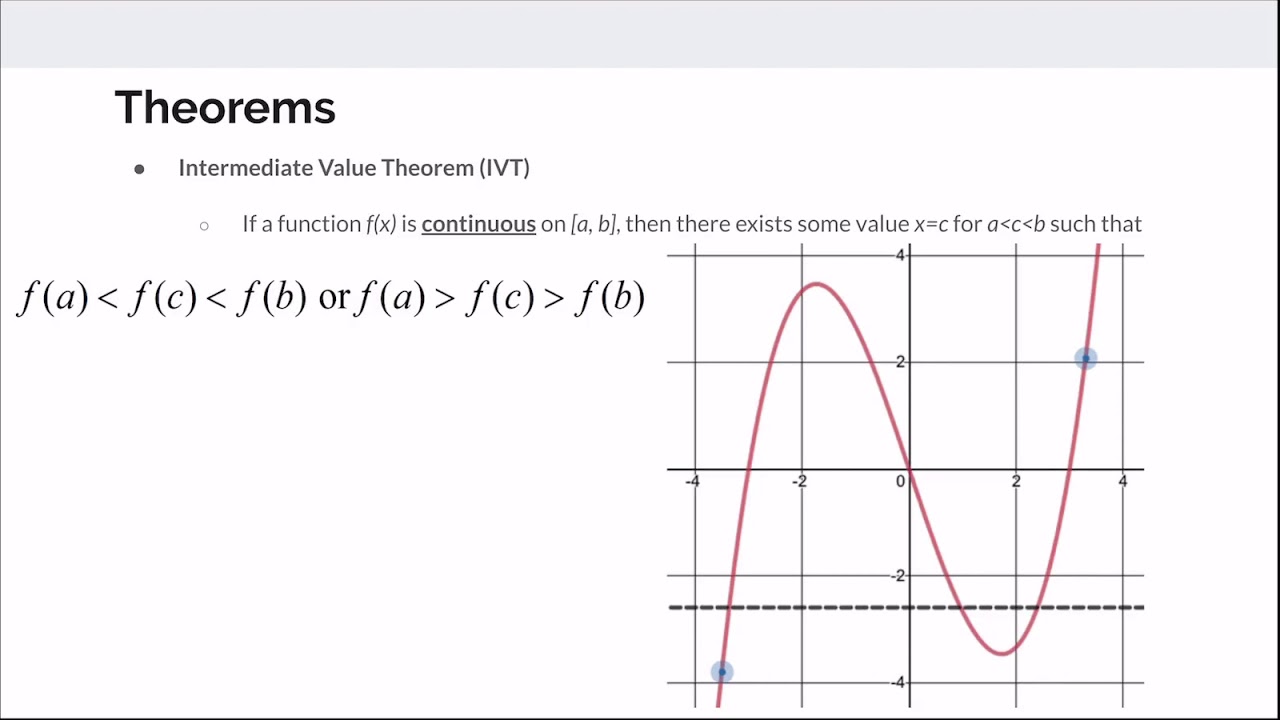
Given a table of selected values for a twice differentiable function f, which of the following must be true?
-Since the function is twice differentiable, it is continuous and its derivative is also continuous. However, without specific information about the behavior of the function between the table values, broad statements about the function's critical points or the sign of its second derivative are speculative. The most justifiable conclusion from the given data would be that the derivative of the function takes on all values between its minimum and maximum rates of change within the given intervals, by the mean value theorem and the intermediate value theorem.
Outlines
📚 AP Calculus AB & BC Review: Problem Set 4
This video provides a comprehensive review of AP Calculus AB and BC multiple-choice questions, based on actual exam problems. The presenter encourages viewers to attempt the problems before watching the solutions. The first question involves finding the time when the velocity of a particle moving along the x-axis, described by a specific function, is zero. The solution involves calculus and trigonometry, emphasizing the importance of knowing the unit circle's famous angles. The video continues with a variety of calculus problems, including derivatives, integrals, and limits, each with a detailed walkthrough of the solution process.
🔍 Derivatives and Tangent Line Approximations
The second paragraph focuses on the application of derivatives to find tangent lines and make approximations. It discusses the process of finding the slope of a tangent line using the derivative of a function and then using the point-slope form to write the equation of the tangent line. The presenter also covers a problem involving the approximation of a function's value at a specific point using the tangent line at another point. The importance of knowing the unit circle values is highlighted, as well as the ability to apply the chain rule and use point-slope form for tangent lines.
📈 Understanding Limits and Continuity in Functions
The third paragraph deals with limits, particularly when they do not exist due to discontinuities in functions. It also covers the concept of the derivative as the limit of the average rate of change. The presenter solves a limit problem using l'Hôpital's rule, a method for finding limits of indeterminate forms. The video emphasizes the need to understand the graph of absolute value functions and the ability to apply algebraic techniques such as completing the square and long division in calculus problems.
🧮 Advanced Calculus Techniques: L'Hôpital's Rule and Mean Value Theorem
The fourth paragraph presents a problem that requires the use of l'Hôpital's rule to find a limit that results in an indeterminate form. The presenter demonstrates the process of differentiating the numerator and denominator until a determinate form is obtained. The video also touches on the second fundamental theorem of calculus and the mean value theorem, which are used to analyze the behavior of a function within a given interval. The importance of recognizing when to apply these theorems is stressed.
🔢 Analyzing Function Data and Applying the Intermediate Value Theorem
The final paragraph involves analyzing a table of function values to determine which statements about the function must be true. The presenter uses the intermediate value theorem to justify that the derivative of the function must take on certain values within a given interval. The video concludes with a reminder that while the function is twice differentiable, making broad generalizations without proper justification can be misleading. The presenter advises viewers to be cautious and methodical when approaching such problems.
Mindmap
Keywords
💡AP Calculus
💡Derivative
💡Product Rule
💡Trigonometric Equations
💡Second Fundamental Theorem of Calculus
💡Tangent Line Approximation
💡Absolute Value Function
💡L'Hôpital's Rule
💡Completing the Square
💡Mean Value Theorem
💡Intermediate Value Theorem
Highlights
The video provides a comprehensive review of AP Calculus AB and BC multiple-choice questions.
Problems are based on those that appeared on past AB exams, which could also be on BC exams.
The presenter recommends attempting the problems before watching the video to check understanding.
The first question involves finding the first time a particle's velocity is zero using calculus.
The presenter uses the product rule to avoid the quotient rule in finding the derivative.
The solution to the first problem involves understanding the behavior of exponential functions and trigonometric equations.
The second problem is a straightforward application of the second fundamental theorem of calculus.
For the third problem, the presenter uses the tangent line approximation to find an approximation for a function at a given point.
The video emphasizes the importance of knowing the unit circle and its associated values for trigonometric functions.
The presenter discusses the graph of the absolute value function and its implications for a multiple-choice question.
The concept of a jump discontinuity is introduced as a key feature of the graph in question.
The video demonstrates the use of L'Hôpital's rule for solving limits that result in indeterminate forms.
Completing the square and long division are highlighted as algebraic techniques that may be required for integration.
The presenter uses rational exponents to simplify the expression for a function's derivative in one of the problems.
The video includes a problem that requires the application of the mean-value theorem to determine a property of the derivative.
The presenter advises on the use of the intermediate value theorem to justify a choice in a multiple-choice question.
The video concludes with a reminder to watch other problem sets in the playlist for further practice.
Transcripts
Browse More Related Video

AP Calculus AB 2008 Multiple Choice (No Calculator)

AP Calc AB & BC Practice MC Review Problems #2

AP Calculus BC 2003 Multiple Choice (calculator) - Questions 76 - 92

AP Calculus AB 2012 Multiple Choice (calculator) - Questions 76 - 92
AP Calculus AB Review

AP Calculus Multiple Choice Practice Test (2016 AP CED Problems)
5.0 / 5 (0 votes)
Thanks for rating: