First order, Ordinary Differential Equations.
TLDRThis educational video script offers an in-depth exploration into solving ordinary differential equations (ODEs) with a focus on four primary techniques: separable equations, homogeneous method, integrating factor, and exact differential equations. The script begins by detailing the steps to solve separable equations, showcasing an example and emphasizing the importance of integrating key components. It then transitions into the homogeneous method, illustrating how to verify homogeneity and apply substitution to simplify the equation. The integrating factor technique is next, where the script explains how to identify the integrating factor and apply it to linear ODEs that are neither separable nor homogeneous. Lastly, the script delves into exact differential equations, guiding through the process of standardizing the equation, verifying its exactness, and integrating to find the solution. The video concludes with a bonus section on standard integrals, providing a valuable resource for quick reference. This comprehensive guide is enriched with practical examples and is designed to enhance the viewer's understanding and proficiency in differential equations.
Takeaways
- 📚 Start with Separable Equations: When you have an equation in the form d y/d x = p(x) * q(y), it is considered a separable equation.
- 🔍 Convert y' to dy/dx: The first step in solving separable equations is to express y' as dy/dx.
- ➗ Isolate Variables: Subtract 2xy from both sides and factor out x to isolate the variables.
- 🔄 Integration: Integrate both sides of the separated equation, using substitution for integrals involving ln.
- 🔑 Exact Form: To find the explicit form of the solution, isolate y by manipulating the equation algebraically.
- 🏡 Homogeneous Method: Check if the equation is homogeneous by substituting x with kx and y with ky and see if it equals the original function.
- 🔁 V Substitution: Use v = y/x substitution in homogeneous differential equations and differentiate to get a separable equation.
- 📈 Integrate and Solve for y: After making the equation separable using v substitution, integrate both sides and solve for y to find the explicit form.
- 📝 Integrating Factor: For linear ODEs that are neither separable nor homogeneous, find the integrating factor, μ(x) = e^(∫p(x)dx).
- 🔗 Product Rule: Multiply through by the integrating factor and use the product rule to simplify the left side of the equation.
- ∫ Integration by Parts: Solve for the integrating factor multiplied by the function, often requiring integration by parts for functions like x * e^x.
- 📉 Exact Differential Equations: For an equation to be an exact differential equation, ∂m/∂y must equal ∂n/∂x, where m and n are the separated variable parts of the equation.
- 🔍 Identify m and n: In exact differential equations, m contains the x terms and n contains the y terms, with no cross terms.
- 🧮 Integration for g(y) or h(x): Integrate either m with respect to x plus g(y) or n with respect to y plus h(x) to find the function you need.
- 📌 Constant of Integration: Remember to use a different constant, like k or c1, c2, when integrating to avoid confusion with existing constants in the problem.
- 📐 Standard Integrals: Memorize standard integrals for exponential, trigonometric, inverse trigonometric, and hyperbolic functions for quick reference.
Q & A
What are the four techniques discussed in the video for solving ordinary differential equations?
-The four techniques discussed in the video are separable equations, homogeneous method, integrating factor, and exact differential equations.
What is the form of a separable equation in differential calculus?
-A separable equation has the form d y/d x = p(x) * q(y), where p(x) is a function of x and q(y) is a function of y.
How do you convert a separable equation into a form that allows for integration?
-To convert a separable equation for integration, you divide both sides by p(x)q(y), which isolates the variables and allows you to integrate each side with respect to their respective variables.
What is the purpose of the integrating factor in solving linear ordinary differential equations?
-The integrating factor is used to make the left side of a linear differential equation, when multiplied by it, into a perfect derivative, which simplifies the process of finding the solution to the differential equation.
How do you check if a differential equation is homogeneous?
-To check if a differential equation is homogeneous, you replace x with kx and y with ky in the original function and see if the new function is proportional to the original function.
What is the formula to find the integrating factor, μ(x), in the method of integrating factor?
-The formula to find the integrating factor, μ(x), is μ(x) = e^(∫p(x) dx), where p(x) is the coefficient of y in the given differential equation.
What is the standard form of an exact differential equation?
-The standard form of an exact differential equation is M(x, y) dx + N(x, y) dy = 0, where M(x, y) and N(x, y) are functions of x and y.
How do you use the method of separation of variables to solve the given example y' + 2xy = x?
-First, divide both sides by x to separate the variables. Then, subtract 2xy from both sides and factor out x. After that, multiply both sides by dx and divide by (1 - 2y) to separate the variables completely. Finally, integrate both sides with respect to their own variables.
What is the role of the substitution v = y/x in the homogeneous method?
-The substitution v = y/x is used to transform the homogeneous differential equation into a separable equation. It simplifies the equation by reducing it to a form where the terms involving x and y are separated and can be individually integrated.
What is the process to solve an exact differential equation after identifying M(x, y) and N(x, y)?
-After identifying M(x, y) and N(x, y), you check if the equation is exact by comparing the partial derivatives of M with respect to y and N with respect to x. If they are equal, you integrate either M with respect to x or N with respect to y, add an arbitrary function of the other variable, and then differentiate partially to solve for the function, which when integrated gives the solution to the differential equation.
How do you use integration by parts to solve the integral of x * e^x with respect to x?
-Integration by parts is used when the integral is a product of two functions, one of which is easily integrable and the other easily differentiable. You choose u to be the differentiable function (x in this case) and dv to be the integrable function (e^x in this case). Then apply the formula ∫u dv = u∫v du - ∫(du)(∫v), which simplifies to ∫x * e^x dx = x * e^x - ∫e^x dx, and proceed with the integration.
Outlines
📚 Introduction to Solving ODEs
The video introduces four techniques for solving ordinary differential equations (ODEs): separable equations, homogeneous method, integrating factor, and exact differential equations. It begins with the concept of separable equations, which are solved by isolating variables and integrating. The example given is a first-order linear ODE, which is solved step by step, illustrating the process of converting the equation into a separable form, integrating both sides, and using substitution to find the general solution.
🔍 Homogeneous Method Overview
The video explains the homogeneous method, which is applicable when the differential equation is homogeneous. The method involves checking for homogeneity by substituting x with kx and y with ky, and then solving the equation using v-substitution where v equals y/x. The process includes differentiating the substitution, simplifying the equation into a separable form, and integrating to find the solution. An example of a homogeneous differential equation is provided, and the steps to solve it are outlined.
🧐 Homogeneous Differential Equation Solution
This paragraph delves into solving a specific homogeneous differential equation. It demonstrates the steps of substituting x with kx and y with ky to check for homogeneity, performing v-substitution, and then differentiating and simplifying the equation. The solution process involves separating the variables, integrating both sides, and substituting back to find the explicit form of the solution. The importance of understanding the differentiation of the substitution and the integration techniques is emphasized.
📝 Steps for Homogeneous Method
The video outlines the steps for solving ODEs using the homogeneous method, emphasizing the need to check if the function is homogeneous by substituting kx and ky. It details the process of dividing all terms by the highest power of x, performing v-substitution, differentiating, simplifying, and converting the equation into a separable form. The integration of both sides and the substitution of v back into the equation to find the implicit and explicit forms of the solution are also covered.
🧬 Integrating Factor Technique
The integrating factor technique is introduced for solving ODEs that are neither separable nor homogeneous but fit a specific form involving the derivative of y and a function of x. The video explains how to identify the integrating factor, which is the exponential of the integral of the coefficient of y. The process includes multiplying the entire equation by the integrating factor, applying the product rule, and integrating both sides to find the solution. An example is worked through, demonstrating the calculation of the integrating factor and the steps to solve the ODE.
🧠 Integration by Parts
The video discusses the use of integration by parts in solving differential equations, presenting both the tabular method and the formula method. It shows how to select the appropriate functions for u and dv, perform the integration, and apply the method to find the integral of a product of functions. The process is illustrated through an example, highlighting the practicality and efficiency of the tabular method for finding the integral of x times e to the x.
🔗 Exact Differential Equations
The video explains the concept of exact differential equations and how to identify them by ensuring the given equation is in the standard form involving m(x, y) and n(x, y). It demonstrates the process of checking for exactness by comparing the partial derivatives of m with respect to y and n with respect to x. If they are equal, the equation is exact, and the video outlines the steps for integrating either m or n, differentiating the integrated result, and solving for the function of the other variable.
🔑 Integration for Exact ODEs
This paragraph focuses on the integration process for exact ODEs. It describes integrating either m with respect to x or n with respect to y, adding an arbitrary function of the other variable, and differentiating partially to solve for the arbitrary function. The goal is to find an implicit solution by setting the integrated function equal to a constant. The process is illustrated with an example, emphasizing the importance of comparing the differentiated function to the other half of the original equation.
📚 Standard Integrals and Derivatives
The video concludes with a bonus section on standard integrals, providing a list of useful integrals for exponential, trigonometric, inverse trigonometric, and hyperbolic functions. It also offers a mnemonic technique for remembering the derivatives and anti-derivatives of trigonometric functions using a clockwise and anti-clockwise direction metaphor. The presenter thanks the viewers and invites them to join the next video.
Mindmap
Keywords
💡Separable Equations
💡Homogeneous Method
💡Integrating Factor
💡Exact Differential Equations
💡v-Substitution
💡Product Rule
💡Integration by Parts
💡Implicit Form
💡Explicit Form
💡Standard Integrals
Highlights
The video introduces four key techniques for solving ordinary differential equations: separable equations, homogeneous method, integrating factor, and exact differential equations.
Separable equations are solved by isolating variables and integrating, as demonstrated with the example of y' + 2xy = x.
The homogeneous method requires checking if the given function is homogeneous by substituting x with kx and y with ky.
An example of the homogeneous method is solving dy/dx = (x^2 + y^2) / (x*y) using v-substitution and separation of variables.
The integrating factor technique is applicable for equations that are neither separable nor homogeneous, demonstrated with dy/dx + y = x.
The integrating factor, μ(x), is found using the formula e^(∫p(x)dx), where p(x) is the coefficient of y in the differential equation.
Exact differential equations are solved by ensuring the equation is in the standard form M(x, y)dx + N(x, y)dy = 0 and checking for exactness through partial derivatives.
An example of an exact differential equation is given as 3x^2 + 1 + 3y^2 + 2y(dy/dx) = 0, which is solved by integrating one side of the equation.
Integration by parts is a crucial technique used in solving differential equations, with both tabular and formula methods demonstrated.
The video emphasizes the importance of being fluent with integration techniques, as they form the backbone of solving differential equations.
The explicit form of a solution is obtained by isolating y, as shown in the examples throughout the video.
The video provides a comprehensive recap of each method, ensuring the viewer has a clear understanding of the steps involved in solving differential equations.
The presenter recommends memorizing certain standard integrals for quick reference when solving differential equations.
A list of back pocket integrals is provided, including exponential, trigonometric, inverse trigonometric, and hyperbolic functions.
The video concludes with a mnemonic technique for remembering the derivatives and anti-derivatives of trigonometric functions.
The presenter thanks the viewers and invites them to the next video, indicating a series of educational content.
Transcripts
Browse More Related Video

Linear Differential Equations & the Method of Integrating Factors

SC_V1_2 Integrating Factor to Solve Linear ODEs

Integrating Factor for Exact Differential Equations (Differential Equations 30)

Homogeneous Differential Equations

Separable differential equations introduction | First order differential equations | Khan Academy
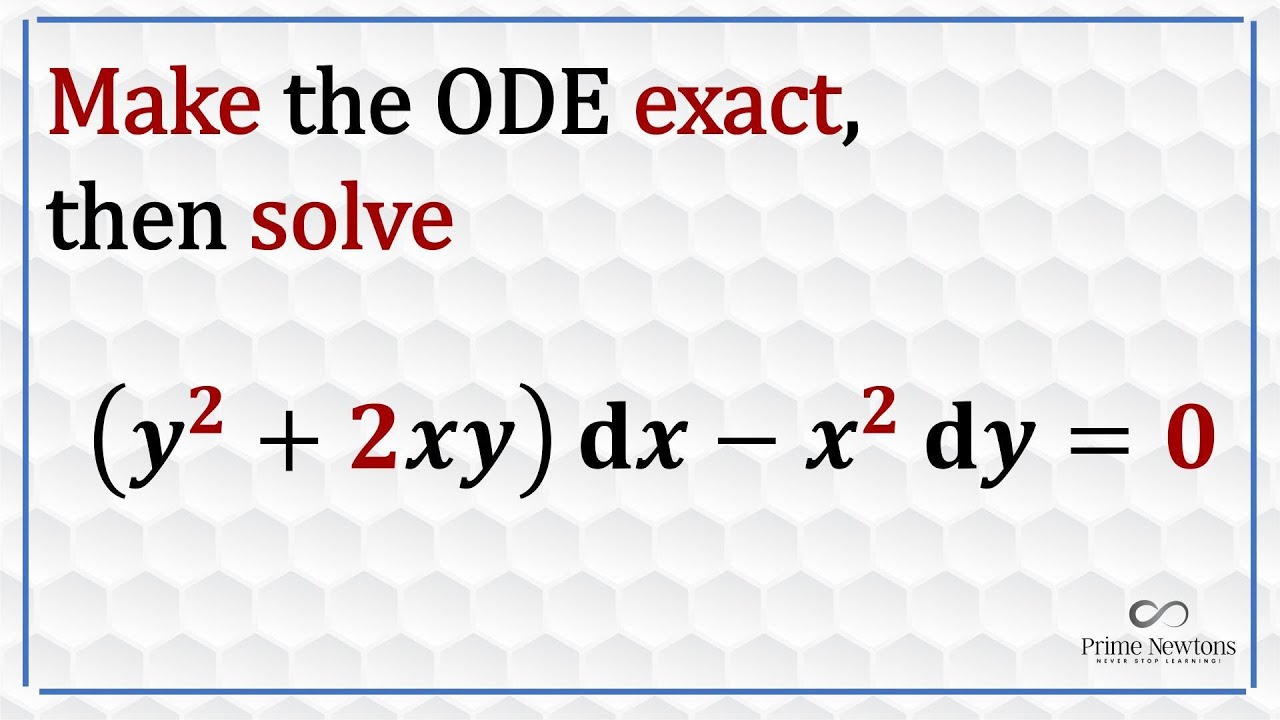
How to solve exact and non-exact ODE
5.0 / 5 (0 votes)
Thanks for rating: