Integrating Factor for Exact Differential Equations (Differential Equations 30)

Professor Leonard

27 Mar 201975:55

EducationalLearning

32 Likes 10 Comments

TLDRThe video delves into the concept of exact differential equations, emphasizing the importance of understanding their properties and how to solve them. It introduces a specific technique using an integrating factor to transform non-exact differential equations into exact ones, allowing for easier solution. The process involves checking mixed partial derivatives for equality, selecting the appropriate integrating factor based on the variables involved, and applying it to the equation. The video provides a step-by-step explanation, complete with examples and the application of the product rule, making it an informative resource for those seeking to grasp the intricacies of differential equations.

Takeaways

📚 The video discusses the concept of exact differential equations and introduces a specific technique for solving non-exact differential equations using an integrating factor.
🔍 It emphasizes the importance of understanding the background of exact differential equations before delving into this advanced technique.
🎯 The main focus is on how to identify and apply an integrating factor that can transform a non-exact differential equation into an exact one, making it solvable using known methods.
🌟 The video provides a detailed explanation of the theoretical underpinnings of integrating factors, including the conditions under which they can be applied.
📌 It highlights the need to check mixed partial derivatives for equality to determine if a differential equation is exact and how to find an integrating factor if it is not.
📈 The process involves taking the partial derivative of the equation's components with respect to the respective variables and comparing them to identify the correct integrating factor.
🔧 The video walks through the steps of solving for the integrating factor, including the algebraic manipulation and grouping of terms necessary to isolate the variable of interest.
📝 Examples are provided to illustrate the process of finding an integrating factor and solving the differential equation after its application.
🚫 The video warns about potential issues with missing or extra solutions when using integrating factors, particularly in cases of singular solutions.
🤔 The presenter encourages viewers to think critically about the process and to verify each step to ensure the correct application of the integrating factor.
🌐 The video concludes with a reminder of the importance of understanding the theory behind mathematical techniques to effectively apply them in problem-solving.

Q & A

What is the main topic of the video?
-The main topic of the video is about solving differential equations, specifically focusing on exact differential equations and the use of integrating factors.
What is an exact differential equation?
-An exact differential equation is a type of differential equation that can be written as the total differential of a function, meaning it can be expressed as the differential of some potential function.
What is an integrating factor and what is its purpose?
-An integrating factor is a function, usually denoted by U(x, y), that is used to transform a non-exact differential equation into an exact one. It simplifies the process of solving the differential equation by making the mixed partial derivatives equal.
How does one determine if a differential equation is exact?
-To determine if a differential equation is exact, one must check if the mixed partial derivatives of the functions M and N with respect to x and y are equal. If they are not equal, the equation is not exact.
What is the process of finding an integrating factor?
-The process of finding an integrating factor involves taking the difference of the mixed partial derivatives of M and N, dividing by the function that appears in the denominator of the non-exact differential equation, and then integrating with respect to either x or y to find the factor.
What is the significance of the product rule in this context?
-The product rule is significant in the process of finding an integrating factor because it is used to expand the differential equation when multiplying both sides by the integrating factor, which is necessary to transform it into an exact differential equation.
How does the video emphasize the importance of background knowledge in understanding the topic?
-The video emphasizes the importance of background knowledge by stating that understanding exact differential equations requires familiarity with terminology and concepts that might not make sense without prior knowledge. It suggests watching previous videos for a better grasp of the subject.
What is the role of the integrating factor in the process of solving differential equations?
-The integrating factor plays a crucial role in the process by allowing the transformation of a non-exact differential equation into an exact one. This transformation simplifies the equation, making it easier to solve using techniques learned in previous lessons.
What happens when the integrating factor only contains x's or only y's?
-When the integrating factor only contains x's or only y's, it simplifies the process of solving the differential equation. The partial derivative with respect to the other variable becomes zero, and the derivative with respect to the variable present in the integrating factor is no longer a partial derivative but a regular derivative, which simplifies the equation further.
How does the video address the potential for missing solutions when using integrating factors?
-The video mentions that when using integrating factors to solve differential equations, there is a possibility of gaining extra solutions or not finding all solutions, such as singular solutions. It advises viewers to be cautious and aware of this potential issue.

Outlines

00:00

📚 Introduction to Solving Differential Equations

The speaker begins by introducing the topic of exact differential equations, emphasizing the importance of understanding previous videos on the subject. They mention a specific technique for solving certain differential equations that are not exact and introduce the concept of an integrating factor. The speaker also highlights the need for background knowledge on exact differential equations to fully grasp the upcoming content.

05:01

🔍 Analyzing Non-Exact Differential Equations

The speaker delves into the process of analyzing differential equations that are not exact, discussing the conditions under which a differential equation can be considered exact. They explain the concept of mixed partials and how their equality is crucial for an equation to be exact. The speaker also introduces the idea of transforming a non-exact equation into an exact one by multiplying it by a function, which is the main focus of the video.

10:03

🧩 Solving for the Integrating Factor

The speaker explains the process of solving for the integrating factor, which simplifies the differential equation. They discuss the possibility of finding a function that, when multiplied by the original equation, results in an exact differential equation. The speaker also introduces the concept of partial derivatives with respect to X and Y, and how they relate to the integrating factor.

15:05

📈 Working with Partial Derivatives

The speaker continues to elaborate on the role of partial derivatives in solving differential equations. They provide a detailed explanation of how to manipulate partial derivatives to align with the requirements of an exact differential equation. The speaker also introduces the product rule and its application in this context, further illustrating the process of solving for the integrating factor.

20:05

🔧 Applying the Integrating Factor

The speaker discusses the application of the integrating factor to the differential equation. They explain how to determine whether the integrating factor should be a function of X or Y, based on the simplification of the equation. The speaker also provides a formula for finding the integrating factor and emphasizes the importance of understanding the theory behind the process.

25:06

🌟 Transforming Non-Exact to Exact Differential Equations

The speaker explains the process of transforming a non-exact differential equation into an exact one by applying the integrating factor. They provide a step-by-step guide on how to check the mixed partials and determine the correct integrating factor. The speaker also discusses the implications of the integrating factor on the domain of the equation and how to proceed with the solution once the equation is made exact.

30:08

📝 Example: Solving a Non-Exact Differential Equation

The speaker presents an example of a non-exact differential equation and demonstrates the process of solving it using the integrating factor. They walk through the steps of checking the mixed partials, finding the integrating factor, and transforming the equation into an exact form. The speaker also corrects a mistake made in a previous example, highlighting the importance of checking work for accuracy.

35:10

🎓 Final Thoughts on Integrating Factors

The speaker concludes the video by summarizing the process of using integrating factors to solve differential equations. They emphasize the importance of understanding the theory behind the process and the potential for missing or gaining solutions when using this technique. The speaker also mentions future videos on real-life applications of these concepts.

Mindmap

Keywords

💡Exact Differential Equations

Exact differential equations are a type of differential equation that can be written as the total differential of a function, indicating that the equation arises from a potential function that is continuous and differentiable in a region. In the video, the speaker discusses how to identify and solve these equations using integrating factors when they are not initially in exact form.

💡Integrating Factors

Integrating factors are multiplicative functions used to transform a non-exact differential equation into an exact one. They are crucial in solving differential equations that do not initially meet the criteria for exactness. The speaker explains the process of finding an integrating factor by comparing partial derivatives and integrating to find the factor that makes the equation exact.

💡Partial Derivatives

Partial derivatives are derivatives that deal with multivariable functions, calculating the rate of change with respect to one variable while holding all other variables constant. In the context of the video, partial derivatives are used to check if a differential equation is exact and to find integrating factors.

💡Mixing Partials

Mixing partials is a term used to describe the process of taking the partial derivative of one function with respect to another variable, such as the partial derivative of M with respect to Y and the partial derivative of N with respect to X. The equality of mixing partials is a criterion for a differential equation to be exact.

💡Potential Function

A potential function is a function from which an exact differential equation can be derived. It is a function that has continuous and differentiable properties in a certain region. The video discusses how to find such a function by transforming a non-exact differential equation into an exact one using integrating factors.

💡Differential Equation

A differential equation is an equation that relates a function with its derivatives. It is a fundamental part of calculus and is used to describe various phenomena in fields like physics and engineering. The video focuses on a specific type of differential equation, exact differential equations, and their solutions.

💡Integration

Integration is a mathematical process that is the reverse of differentiation. It involves finding a function whose derivative is a given function. In the context of the video, integration is used to find the integrating factor and to solve the differential equation after making it exact.

💡Separation of Variables

Separation of variables is a method used to solve first-order differential equations by rearranging the equation so that all terms involving one variable are on one side and all terms involving the other variable are on the other side. This technique is not directly discussed in the video, but it is related to the process of solving differential equations.

💡Constant

In the context of differential equations, a constant is a term that does not change with the variables being manipulated. It often appears in the final solution of a differential equation, representing an arbitrary value that can be determined based on initial conditions or boundary values.

💡Domain Restrictions

Domain restrictions refer to the set of allowable values for the independent variable(s) in a function. These restrictions are often necessary when solving differential equations to ensure that the solution is valid and that the variables remain within a certain range.

Highlights

The video introduces a specific technique for solving certain differential equations that are not exact.

The importance of understanding the previous videos on exact differential equations is emphasized for context.

The concept of an integrating factor is discussed, which simplifies the form of a differential equation.

The video explains how to identify if a differential equation is exact by checking if the mixed partials are equal.

A method for finding an integrating factor when the differential equation is not exact is presented.

The process of multiplying the differential equation by an integrating factor to make it exact is demonstrated.

The video clarifies that the integrating factor must be carefully chosen based on the variables involved.

The theoretical underpinnings of why the integrating factor works are explored in detail.

The video provides a step-by-step guide on how to apply the integrating factor to specific cases.

The concept of partial derivatives and how they relate to the integrating factor is explained.

The video emphasizes the importance of checking the mixed partials after applying the integrating factor.

The process of solving the differential equation after applying the integrating factor is outlined.

The video discusses the potential for extra solutions or missed solutions when using integrating factors.

The practical application of integrating factors in solving real-world problems is mentioned as a topic for future discussion.

The video concludes with a summary of the key points and the process for solving non-exact differential equations using integrating factors.

Transcripts

Browse More Related Video

First order, Ordinary Differential Equations.

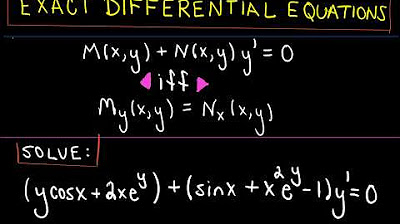
Exact Differential Equations

What are Exact Differential Equations (Differential Equations 28)

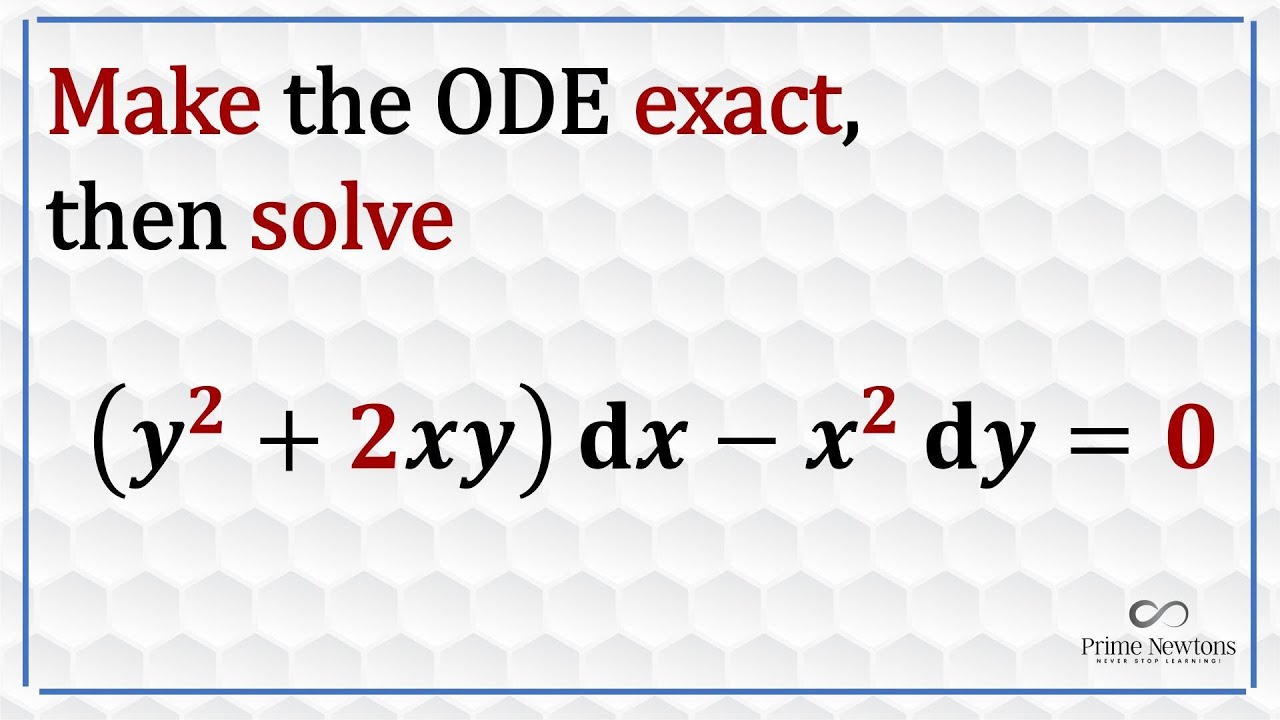
How to solve exact and non-exact ODE

Linear Differential Equations & the Method of Integrating Factors

Introduction to Linear Differential Equations and Integrating Factors (Differential Equations 15)

Related Tags

Differential Equations Integrating Factors Mixed Partials Mathematical Analysis Exact Equations Non-Exact Equations Solving Techniques Educational Content Mathematics Tutorial Advanced Math