How to solve exact and non-exact ODE
TLDRThe video script presents a comprehensive guide on solving exact differential equations, a topic requested by viewers. The host explains the importance of identifying the functions M and N, which are derived from partial differentiation with respect to X and Y. The video walks through the process of determining if an equation is exact by checking if the order of differentiation affects the result, a principle rooted in Clairaut's theorem. If the equation is not exact, the script outlines a method to make it exact using an integrating factor, which depends on the variable with respect to which the non-exactness is identified. The host demonstrates the integration process, emphasizing the need to remember formulas and the importance of correctly identifying dependencies on variables. The final solution involves integrating the exact equation to find the original function F, taking into account the constants and functions that may arise from the integration process. The video concludes by encouraging continuous learning in the field of mathematics.
Takeaways
- 📚 The video discusses how to solve exact differential equations and the steps involved in handling them, whether they are already exact or need to be made exact through an integrating factor.
- 🔍 To identify if an equation is exact, one must check if the order of differentiation with respect to X and Y yields the same result, as per Clairaut's theorem.
- ✅ The key to solving an exact equation is to correctly identify 'M' and 'N', which are the partial derivatives of the function F with respect to X and Y, respectively.
- 🚫 If the partial derivatives of M with respect to Y and N with respect to X are not equal, the equation is not exact.
- 🔑 An integrating factor can be used to make a non-exact equation exact. It is crucial to remember the formula for the integrating factor, which depends on whether 'M' or 'N' is manipulated.
- ⚖️ The integrating factor should only depend on one variable (either X or Y) for the equation to be made exact. If it depends on both, a different approach is needed.
- 🧮 After finding a valid integrating factor, it is multiplied by the original equation to make it exact. This step is crucial before proceeding to solve the equation.
- 🧲 Once the equation is made exact, it is solved by integrating the terms associated with 'M' and 'N', taking into account the constants that may arise from partial differentiation.
- 🔠 The final solution is found by integrating the terms and accounting for the original function 'F', which may include an additional function of X, denoted as 'h of X'.
- 📝 It is important to note that constants arising from integration should be treated as functions of the variable not involved in the integration process to maintain accuracy.
- 💡 The video emphasizes the importance of understanding the process of making an equation exact and solving it, rather than just memorizing formulas, to truly grasp the concept of differential equations.
Q & A
What is the primary focus of the video?
-The video focuses on solving differential equations, specifically exact differential equations, and covers the steps to solve them, including how to make a non-exact equation exact and then solve it.
What are the two functions, M and N, in the context of exact differential equations?
-M and N are functions that represent the parts of an exact differential equation. M is the function that has been partially differentiated with respect to X, and N is the function that has been partially differentiated with respect to Y.
How does one determine if a differential equation is exact?
-To determine if a differential equation is exact, one must check if the partial derivative of M with respect to Y is equal to the partial derivative of N with respect to X. If they are equal, the equation is exact.
What is the role of Clairaut's theorem in the context of exact differential equations?
-Clairaut's theorem states that the order of differentiation does not matter. It is used to confirm the exactness of a differential equation by checking if differentiating M with respect to Y yields the same result as differentiating N with respect to X.
If a differential equation is not exact, what is the next step?
-If a differential equation is not exact, the next step is to try and make it exact by finding an integrating factor. The integrating factor is a function that, when multiplied by the original equation, makes it exact.
How does one find an integrating factor for a non-exact differential equation?
-To find an integrating factor, one must identify if the equation can be made exact by multiplying with a function that depends only on X or only on Y. This involves trial and error with different formulas until an integrating factor is found that makes the equation exact.
What is the integrating factor derived in the video?
-The integrating factor derived in the video is e to the integral of -2/y dy, which simplifies to 1/y^2.
How is the integrating factor applied to the original differential equation?
-The integrating factor is multiplied by each term in the original differential equation, which then allows the equation to be treated as exact, making it solvable.
What is the general approach to solving an exact differential equation after applying the integrating factor?
-After applying the integrating factor, one integrates the resulting equation with respect to the variable associated with the integrating factor (either X or Y), to find the original function F that was partially differentiated to generate the equation.
How does one handle the constant of integration when solving a differential equation?
-The constant of integration is typically denoted as C and is included in the final solution. However, when dealing with partial derivatives, it is considered a function of the other variable, so it is represented as a function, such as h(X) or g(Y), rather than a simple constant.
What is the final form of the solution to the differential equation presented in the video?
-The final form of the solution is F(X, Y) = X^2/Y + h(X), where h(X) is an arbitrary function of X, which could be a constant or a more complex function depending on the context of the problem.
Outlines
📚 Introduction to Exact Differential Equations
The video begins with an introduction to exact differential equations, explaining the importance of understanding the steps to solve them. It emphasizes the need to identify 'M' and 'N' in the equation, which are the parts differentiated with respect to 'X' and 'Y', respectively. The video also discusses the concept of an exact equation and how to determine if an equation is exact by checking the order of differentiation using Clairaut's theorem.
🔍 Checking for Exactness and Making It Exact
The second paragraph delves into the process of checking if a given differential equation is exact. It explains that if the partial derivatives with respect to 'X' and 'Y' are not equal, the equation is not exact. The video then introduces the method of making a non-exact equation exact by using an integrating factor that depends solely on 'Y'. The process involves manipulating the equation and applying the integrating factor to transform the equation into an exact form.
🧮 Applying the Integrating Factor
In this part, the video demonstrates how to apply the integrating factor to the original equation. It shows the step-by-step process of multiplying the equation by the integrating factor and simplifying it to an exact form. The video also verifies the exactness by differentiating the new equation with respect to 'X' and 'Y', ensuring both sides are equal.
🧬 Integrating Back to the Original Function
The fourth paragraph focuses on integrating the exact equation back to find the original function 'F'. It discusses the integration process with respect to 'Y', treating 'X' as a constant. The video then explains how to handle the integration results and the importance of considering the original function's dependency on 'X'. It also introduces a new function 'h of X' and shows how to find it by differentiating the integrated function with respect to 'X'.
🎓 Conclusion and Final Thoughts
The final paragraph wraps up the video by summarizing the steps taken to make a non-exact equation exact and then solve it. It encourages viewers to leave comments if they have further questions or topics they'd like to explore. The video ends with a motivational note, emphasizing the importance of continuous learning.
Mindmap
Keywords
💡Differential Equations
💡Exact Differential Equation
💡Partial Derivatives
💡Integrating Factor
💡Claro's Theorem
💡Integration
💡Natural Logarithm
💡Differentiation
💡Constants
💡Function of X and Y
💡Exactness Check
Highlights
The video discusses solving exact differential equations, including steps for when an equation is not exact and how to make it exact.
Differentiating M and N with respect to X and Y is crucial to determine if an equation is exact.
Claro's theorem is mentioned, emphasizing that the order of differentiation does not affect the result if the equation is exact.
If an equation is not exact, an integrating factor can be used to make it exact.
The integrating factor depends on whether the differentiation is with respect to X or Y.
The process of finding an integrating factor involves trial and error until a factor that makes the equation exact is found.
The integrating factor is applied to the original equation to make it solvable.
After applying the integrating factor, the equation is rechecked for exactness before solving.
The solution process involves integrating the equation with respect to Y to find the original function F.
Partial derivatives are taken to find the function h(X), which is part of the original function F.
The final solution includes isolating Y and can be expressed in terms of X and a constant C.
The video emphasizes the importance of not mixing up the order of differentiation and the roles of M and N.
The concept of an exact equation is tied to the equation of a circle, where differentiation yields zero.
The video provides a step-by-step guide on how to solve differential equations, ensuring a comprehensive understanding.
The role of memorizing formulas is highlighted for solving differential equations that are not exact initially.
The video demonstrates the practical application of integrating factors in transforming non-exact equations into solvable forms.
The final solution to the differential equation is presented in terms of X, Y, and a function h(X).
The video concludes with an encouragement to never stop learning, emphasizing continuous education in the field of mathematics.
Transcripts
Browse More Related Video
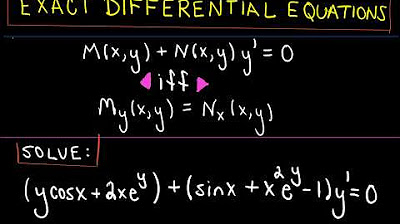
Exact Differential Equations

First order, Ordinary Differential Equations.

Integrating Factor for Exact Differential Equations (Differential Equations 30)

Linear Differential Equations & the Method of Integrating Factors

Partial Derivatives - Multivariable Calculus
MultiVariable Calculus - Implicit Differentiation
5.0 / 5 (0 votes)
Thanks for rating: