What is the Fibonacci Sequence & the Golden Ratio? Simple Explanation and Examples in Everyday Life

Science ABC
23 Apr 202105:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explores the fascinating Fibonacci sequence, a series of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. This mathematical pattern, named after Leonardo Pisano Fibonacci, is found in diverse areas including nature, where it governs the arrangement of petals in flowers and the spirals in seeds and cacti. The script also delves into the golden ratio, an offshoot of the Fibonacci sequence, which is approximately 1.618033... and is observed in various natural phenomena and man-made structures. The golden ratio is known for its aesthetic appeal and is often used in art and architecture. The video invites viewers to observe and share their own examples of the Fibonacci sequence or the golden ratio in their lives, highlighting its pervasive influence across different domains.

Takeaways
  • 🌼 The number of petals on many flowers often follows the Fibonacci sequence, which includes numbers like 3, 5, 8, 13, 21, etc.
  • 🌡 Both cacti leaves and sunflower seeds are arranged in spirals that typically follow the Fibonacci sequence.
  • 🀲 Humans have 2 hands with 5 fingers each, and each finger is divided into 3 parts, all of which are Fibonacci numbers.
  • πŸ“ The lengths of the bones in our hands are also Fibonacci numbers, indicating the sequence's prevalence in human anatomy.
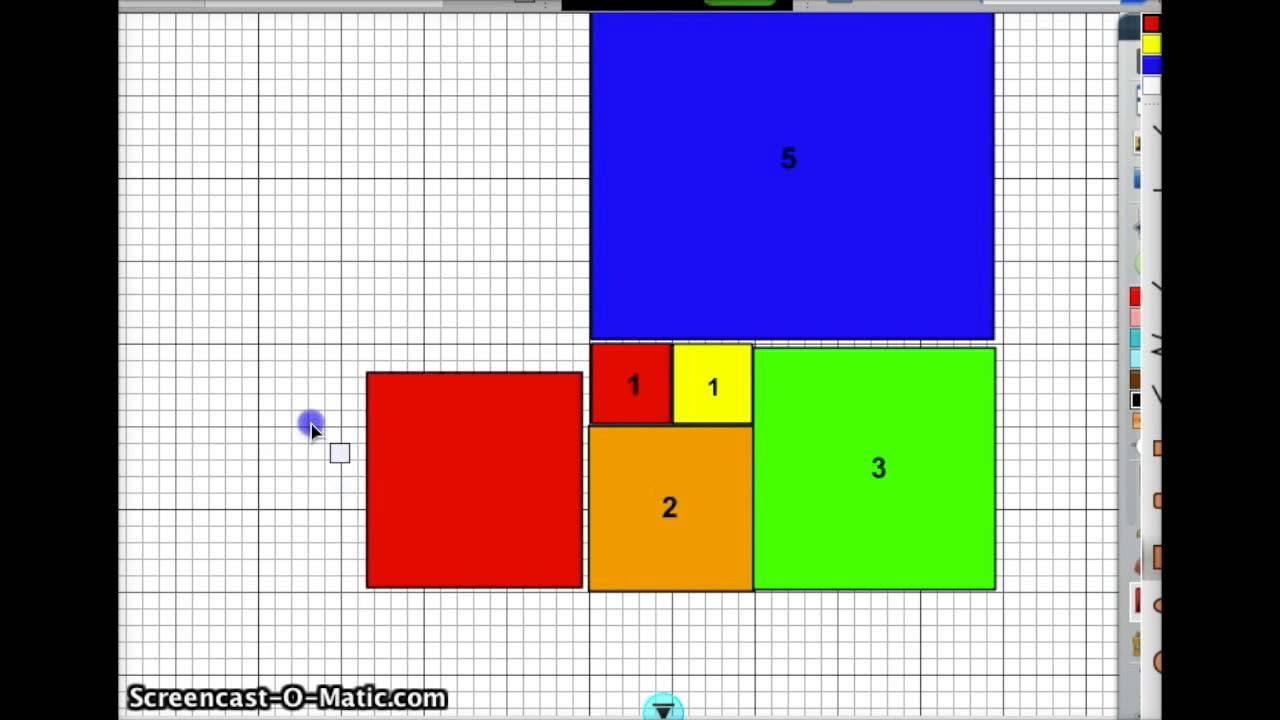
  • πŸ”’ The Fibonacci sequence is defined as each number being the sum of the two preceding ones, starting from 0 and 1.
  • πŸ“œ The Fibonacci sequence is mathematically represented by the formula F(n) = F(n-1) + F(n-2) for n > 1.
  • πŸ“š Leonardo Pisano, known as Fibonacci, introduced the Hindu-Arabic numeral system to the Western world through his book Liber Abaci in 1202.
  • 🌐 The Fibonacci sequence has been described in ancient Indian texts dating back to the 6th century.
  • 🌟 The Fibonacci sequence is closely related to the golden ratio, represented by the Greek letter phi (Ο•), which is approximately 1.618033...
  • 🎨 The golden ratio and golden spirals are found in various aspects of art, architecture, and nature, including seashells, ocean waves, and building designs.
  • πŸ› Architect Le Corbusier used the golden ratio in his Modulor system for architectural proportions, highlighting its significance in design.
  • ✨ The golden ratio is often referred to as the divine proportion and can be observed in numerous natural and man-made structures, from galaxies to the human ear.
Q & A

  • What is the significance of the Fibonacci sequence in nature?

    -The Fibonacci sequence is often observed in nature, with examples such as the number of petals on flowers, the arrangement of seeds in sunflowers, and the spiral patterns in cacti leaves. These occurrences suggest that the sequence is related to natural growth patterns and the efficient use of space.

  • How does the human hand relate to the Fibonacci sequence?

    -The human hand has a connection to the Fibonacci sequence through the number of fingers and their divisions. We have 2 hands with 5 fingers each, and each finger is divided into 3 parts. Additionally, the lengths of the bones in the hand are also Fibonacci numbers.

  • What is the mathematical formula used to represent the Fibonacci sequence?

    -The Fibonacci sequence is mathematically represented by the formula F(n) = F(n-1) + F(n-2), where n is greater than 1. This formula allows for the calculation of any 'n'th number in the sequence.

  • Who is credited with bringing the Hindu-Arabic numeral system to the Western world?

    -Leonardo Pisano, also known as Fibonacci, is credited with introducing the Hindu-Arabic numeral system to the Western world through his book Liber Abaci in 1202.

  • What is the golden ratio and how is it related to the Fibonacci sequence?

    -The golden ratio, represented by the Greek letter phi (Ο•), is a special number approximately equal to 1.618033. It is derived from the Fibonacci sequence by taking two quantities A and B, where A is greater than B, and calculating the ratio of their sum to A. If this ratio equals the ratio of A to B, then A and B are said to have a golden ratio.

  • How is the golden ratio applied in geometry to create a golden spiral?

    -In geometry, a golden spiral is created by applying the golden ratio as a growth factor. The spiral gets wider by a factor of phi for every quarter turn it makes, resulting in a logarithmic spiral that exhibits the golden ratio properties.

  • What are some examples of the golden ratio and golden spirals in everyday life?

    -Examples of the golden ratio and golden spirals include seashells, ocean waves, hurricanes, flower buds, snail shells, and spider webs. These natural phenomena demonstrate the prevalence of the golden ratio in various forms.

  • How has the golden ratio been used in art and architecture?

    -Artists like Salvador Dali have explicitly used the golden ratio in their works, such as in 'The Sacrament of the Last Supper.' Architects, including Le Corbusier, have also incorporated the golden ratio into their designs, with Le Corbusier using it in his Modulor system for architectural proportions.

  • Why is the golden ratio also known as the divine proportion?

    -The golden ratio is referred to as the divine proportion due to its widespread occurrence in nature, art, architecture, and the human body. Its aesthetically pleasing and mathematically unique properties have led to its association with perfection and divine design.

  • What is the Fibonacci sequence and how does it start?

    -The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. The sequence progresses as follows: 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on.

  • How did Fibonacci introduce the concept of the Fibonacci sequence to the Western world?

    -Fibonacci introduced the concept through his book 'Liber Abaci,' where he compared the Hindu-Arabic numeral system with other systems, such as Roman numerals, and demonstrated how the use of the Hindu-Arabic system made calculations faster and easier.

  • What is the connection between the Fibonacci sequence and the golden ratio?

    -The connection lies in the fact that as you progress through the Fibonacci sequence, the ratio of two consecutive Fibonacci numbers tends to approximate the golden ratio (Ο•). This means that the higher the Fibonacci numbers, the closer their ratio is to 1.618033.

Outlines
00:00
🌼 Fibonacci in Nature and Human Anatomy

The paragraph discusses the prevalence of the Fibonacci sequence in nature, particularly in the arrangement of petals on flowers and the spiral patterns in cacti leaves and sunflower seeds. It also mentions the presence of Fibonacci numbers in human hands and fingers, and the division of finger parts. The Fibonacci sequence is introduced as a series where each number is the sum of the two preceding ones, starting with 0 and 1. The formula F(n) = F(n-1) + F(n-2) for n>1 is provided to calculate any term in the sequence.

Mindmap
Keywords
πŸ’‘Fibonacci number
Fibonacci numbers are a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. They are observed in various natural phenomena and biological structures, such as the arrangement of petals in a flower or the spiral pattern of seeds in a sunflower. In the video, it is mentioned that many flowers have a number of petals that are Fibonacci numbers, demonstrating the sequence's prevalence in nature.
πŸ’‘Fibonacci sequence
The Fibonacci sequence is a mathematical series that follows a specific pattern where each number is the sum of the two preceding ones. It is represented by the formula F(n) = F(n-1) + F(n-2) for n > 1. The sequence starts with 0, 1, 1, 2, 3, 5, 8, 13, and so on. The video discusses how this sequence is not only found in mathematics but also in the natural world, including the human hand, which has 5 fingers and each finger is divided into 3 parts, both of which are Fibonacci numbers.
πŸ’‘Leonardo Pisano (Fibonacci)
Leonardo Pisano, also known as Fibonacci, was an Italian mathematician from the Republic of Pisa. He is credited with introducing the Hindu-Arabic numeral system to the Western world through his book 'Liber Abaci' in 1202. Although the Fibonacci sequence was known in ancient Indian texts, it was Fibonacci's work that brought it to prominence in Europe. The video highlights his influence on the development of mathematics and his fascination with the efficiency of the Hindu-Arabic numeral system.
πŸ’‘Golden ratio
The golden ratio, often denoted by the Greek letter phi (Ο•), is a mathematical ratio that results from dividing a line into two parts so that the ratio of the whole line to the longer part is equal to the ratio of the longer part to the shorter part. The value of the golden ratio is approximately 1.618033. The video explains that when the golden ratio is applied as a growth factor in geometry, it forms a logarithmic spiral known as the golden spiral, which is observed in various natural forms such as seashells and snail shells.
πŸ’‘Golden spiral
A golden spiral is a special kind of logarithmic spiral that increases in size by a factor of the golden ratio (phi) for every quarter turn it makes. It is found in various natural structures and is considered aesthetically pleasing, which is why it is often used in art and architecture. The video mentions that the golden spiral can be observed in seashells, ocean waves, and even in the design of buildings by architects like Le Corbusier.
πŸ’‘Hindu-Arabic numeral system
The Hindu-Arabic numeral system is a decimal (base-10) number system that was developed in the Indian subcontinent and later transmitted to the Islamic world, where it was further refined and then introduced to Europe. This system includes the concept of zero and the use of ten digits (0 through 9) to represent numbers. In the video, it is mentioned that Fibonacci was fascinated by this system and played a significant role in bringing it to the Western world through his book 'Liber Abaci'.
πŸ’‘Liber Abaci
Liber Abaci, or 'Book of Calculation', is a mathematical work by Leonardo Fibonacci, published in 1202. It introduced the Hindu-Arabic numeral system to Europe and also contains the earliest known description of the Fibonacci sequence outside of India. The video discusses how this book compared the Hindu-Arabic system with the Roman numeral system and demonstrated the advantages of the former in terms of calculation efficiency.
πŸ’‘Nature
The video script highlights the prevalence of the Fibonacci sequence and the golden ratio in nature, with examples such as the number of petals on a flower, the arrangement of seeds in sunflowers, and the spiral patterns found in cacti. These natural occurrences demonstrate the intrinsic mathematical patterns that govern growth and form in the natural world.
πŸ’‘Architecture
Architecture is mentioned in the context of the video as a field where the golden ratio and Fibonacci sequence are applied for aesthetic and structural purposes. The video specifically references Swiss-French architect Le Corbusier, who used the golden ratio in his Modulor system for architectural proportion, illustrating the influence of these mathematical concepts in design.
πŸ’‘Art
The video discusses the use of the golden ratio and the Fibonacci sequence in the field of art, noting that many artists, including the legendary painter Salvador Dali, have incorporated these mathematical principles into their creative works. The golden ratio is often associated with aesthetic balance and harmony, making it a popular element in artistic composition.
πŸ’‘Divine proportion
The term 'divine proportion' is another name for the golden ratio, reflecting its perceived harmony and balance. The video mentions that the golden ratio is found in various forms throughout nature and human-made structures, suggesting an inherent beauty and order that has led to its description as 'divine'.
Highlights

Flowers often have a number of petals that correspond to Fibonacci numbers.

Cacti leaves and sunflower seeds are arranged in spirals that follow the Fibonacci sequence.

The human hand has 5 fingers, each divided into 3 parts, and the lengths of the bones are Fibonacci numbers.

The Fibonacci sequence is a series where each number is the sum of the two preceding ones.

Leonardo Pisano, also known as Fibonacci, introduced the Hindu-Arabic numeral system to the Western world.

Fibonacci's Liber Abaci book compared numeral systems and advocated for the efficiency of the Hindu-Arabic system.

The Fibonacci sequence has been described in ancient Indian texts dating back to the 6th century.

The golden ratio is an exciting offshoot of the Fibonacci sequence, represented by the Greek letter phi (Ο•).

The golden ratio approximates to a value close to 1.618033…

The golden spiral, a logarithmic spiral that widens by a factor of phi every quarter turn, is found in nature and art.

Seashells, ocean waves, hurricanes, and spider webs are examples of the golden spiral in nature.

Artists like Salvador Dali and architects like Le Corbusier have used the golden ratio in their works.

The golden ratio is used in architectural design for proportions, as seen in Le Corbusier's Modulor system.

The golden ratio is observed in various natural forms, from snail shells to the human ear, and even galaxies.

The list of examples of the Fibonacci sequence or the golden ratio is ever-growing and pervasive in our lives.

The Fibonacci sequence and golden ratio are found in countless places, earning it the name 'divine proportion'.

Readers are encouraged to share their observations of the Fibonacci sequence or the golden ratio in the comments.

Transcripts

Browse More Related Video

The Fibonacci Sequence: Nature's Code

The Fibonacci Sequence and the Golden Ratio

Golden Ratio = Mind Blown!

The fabulous Fibonacci flower formula

The Golden Ratio: Is It Myth or Math?

ILLUSTRATING SEQUENCES AND SERIES || PRECALCULUS

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Fibonacci SequenceGolden RatioNatural PhenomenaMathematical PatternsLeonardo FibonacciHindu-Arabic NumeralsLiber AbaciDivine ProportionGeometric SpiralsArchitectural DesignArtistic InspirationEveryday Observations