The Fibonacci Sequence: Nature's Code

SciShow
17 Aug 201203:20
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the fascinating world of the Fibonacci sequence, a series of numbers found pervasively in nature, represented by 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on, where each number is the sum of the two preceding ones. Originating from India and popularized by Leonardo of Pisa, known as Fibonacci, the sequence is not only mathematically intriguing but also has a practical efficiency in plant growth, optimizing seed distribution. The script further explores the Golden Ratio, approximately 1.618, which is derived from dividing larger Fibonacci numbers. This ratio, known as Phi, was used by the Greeks to symbolize physical perfection and is observed in various natural patterns, including the spiral arrangements of seeds and shells. The Golden Rectangle, with sides in the ratio of successive Fibonacci numbers, also plays a role in these patterns. The video concludes by emphasizing the beauty and importance of mathematics in understanding the world around us.

Takeaways
  • ๐Ÿงฎ Math is a natural creation, not an invention to torment English majors, and it is ubiquitous in the world around us.
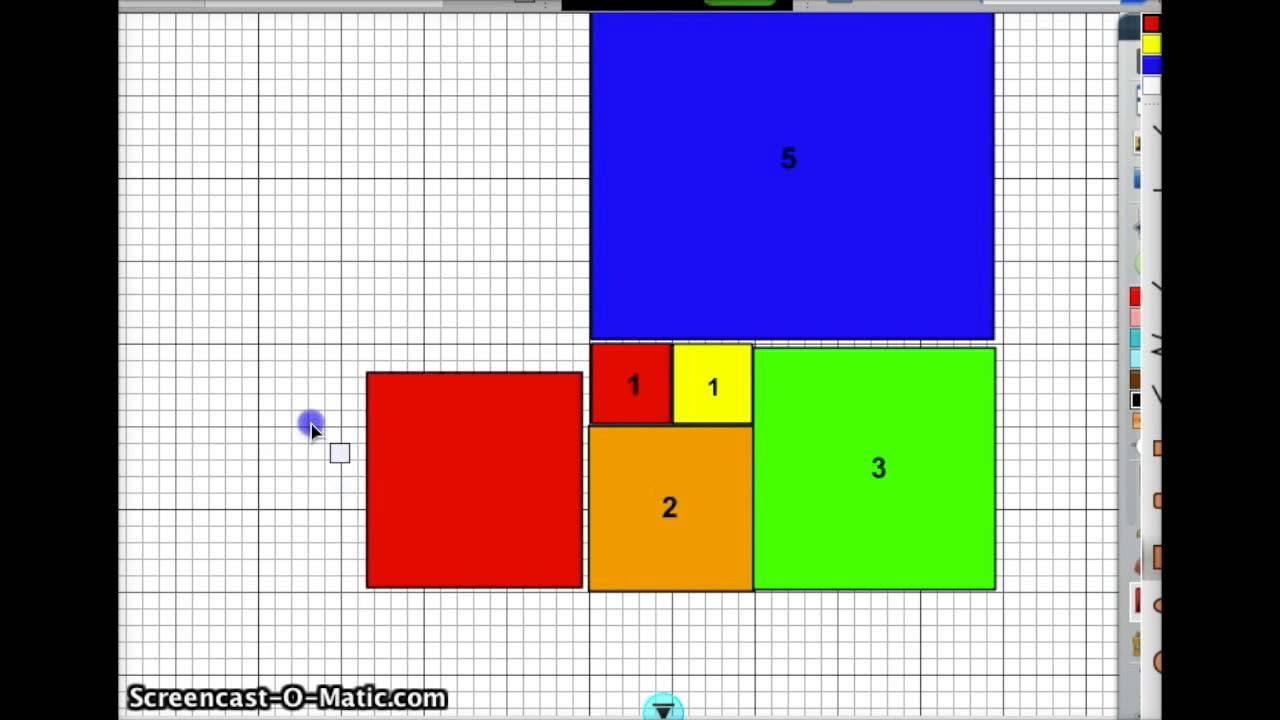
  • ๐ŸŒฟ The Fibonacci Sequence is a set of numbers found frequently in nature, starting with 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on.
  • ๐Ÿ”ข Each number in the Fibonacci Sequence is the sum of the two preceding ones, creating a pattern of addition.
  • ๐Ÿ“š The sequence was first described by Indian mathematicians around 1300 years ago and later introduced to the West by Leonardo of Pisa, known as Fibonacci.
  • ๐Ÿ“– Fibonacci's book, Liber Abaci, introduced the sequence through a thought experiment involving the reproduction of rabbits.
  • ๐ŸŒ In nature, the Fibonacci numbers are evident in the arrangement of plant parts, such as the sections of a banana, the seeds in sunflowers, and the petals of flowers.
  • ๐ŸŒบ Plants exhibit the Fibonacci Sequence not due to a cosmic mandate but because it is the most efficient way to maximize seed packing in a small space.
  • ๐Ÿ“ The Golden Ratio, approximately 1.618..., is a ratio frequently found between successive Fibonacci numbers and has been associated with physical perfection in ancient Greek art.
  • ๐ŸŽจ The Golden Rectangle, with sides in the ratio of consecutive Fibonacci numbers, can be divided into squares with side lengths that are also Fibonacci numbers.
  • ๐ŸŒ€ Drawing arcs from corner to corner of these squares forms a spiral that is reminiscent of natural spirals observed in succulents, pine cones, sunflower seeds, and snail shells.
  • ๐Ÿ“บ The video is from SciShow, an educational channel on YouTube that invites viewers to engage through comments, social media, and subscription for more content.
Q & A

  • What is the Fibonacci Sequence?

    -The Fibonacci Sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. It goes 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on.

  • How was the Fibonacci Sequence first described?

    -The Fibonacci Sequence was first described by mathematicians in India about 1300 years ago and was later introduced to the West in 1202 by Leonardo of Pisa, also known as Fibonacci.

  • What is the significance of Fibonacci numbers in nature?

    -Fibonacci numbers are found in nature in various forms, such as the arrangement of seeds in sunflowers and pine cones, the number of petals on a flower, and the pattern of leaves on a plant stem. They represent an efficient way for plants to pack seeds or grow leaves.

  • Who introduced Arabic numerals to Europe?

    -Leonardo of Pisa, also known as Fibonacci, introduced Arabic numerals to Europe through his work.

  • What is the Golden Ratio, and how is it related to the Fibonacci Sequence?

    -The Golden Ratio, often symbolized by the Greek letter Phi (ฮฆ), is a mathematical ratio of approximately 1.618... It appears when you divide a larger Fibonacci number by the one preceding it, especially noticeable in larger numbers of the sequence.

  • How did the ancient Greeks use the Golden Ratio?

    -The ancient Greeks, including the sculptor Phidias, used the Golden Ratio to represent physical perfection. It was used as a ratio between different parts of statues, such as the statue's total height and the distance from the bottom of its feet to its navel.

  • What is a Golden Rectangle?

    -A Golden Rectangle is a rectangle whose side lengths are successive Fibonacci numbers. It has the property that when divided into squares with side lengths that are also Fibonacci numbers, the squares can be arranged to form a logarithmic spiral similar to those found in nature.

  • In what ways do we observe the Golden Spiral in nature?

    -The Golden Spiral is observed in nature in the spirals of unfolding leaves of a desert succulent, the arrangement of pine cone lobes and sunflower seeds, and the shells of some snails.

  • Why is the arrangement of seeds in sunflowers and pine cones efficient?

    -The arrangement of seeds in sunflowers and pine cones is efficient because it allows for the maximum number of seeds to be packed into a small space, following the pattern of the Fibonacci Sequence.

  • How does the thought experiment involving bunnies relate to the Fibonacci Sequence?

    -The thought experiment involves a pair of bunnies that reproduce to form a new pair, and this process continues, creating a sequence of new bunny pairs that follows the Fibonacci Sequence: 1, 1, 2, 3, 5, 8, and so on.

  • What is the significance of the number 1.618... in the context of the Fibonacci Sequence?

    -The number 1.618... is the approximate value of the Golden Ratio, which is obtained when you divide a Fibonacci number by the one that precedes it in the sequence, especially noticeable with larger numbers.

  • How can one learn more about the mathematical patterns in nature?

    -One can learn more about mathematical patterns in nature by watching educational videos, such as those by Vi Hart, which are often linked in the description of similar content, or by studying related scientific and mathematical literature.

Outlines
00:00
๐ŸŒฟ The Fibonacci Sequence in Nature

This paragraph explains the ubiquitous presence of the Fibonacci sequence in nature. It starts with the basic definition of the sequence and its mathematical pattern, where each number is the sum of the two preceding ones. The sequence was first described by Indian mathematicians and later introduced to the West by Leonardo of Pisa, also known as Fibonacci. The paragraph also discusses the use of the sequence in plant growth, where it is observed in the arrangement of seeds and petals, and how it leads to efficient packing. Additionally, it mentions the Golden Ratio (Phi), a constant ratio derived from Fibonacci numbers, and its historical significance in Greek art and architecture. The Golden Rectangle and its connection to natural spirals are also highlighted.

Mindmap
Keywords
๐Ÿ’กFibonacci Sequence
The Fibonacci Sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. In the context of the video, it is used to illustrate how this mathematical pattern is found in nature, such as the arrangement of seeds in sunflowers and pine cones, as well as the number of petals in flowers. It is a key concept that demonstrates the connection between mathematics and natural phenomena.
๐Ÿ’กGolden Ratio
The Golden Ratio, often denoted by the Greek letter Phi (ฮฆ), is a mathematical constant approximately equal to 1.618. It is derived from the Fibonacci Sequence, where the ratio of two successive Fibonacci numbers tends to this value as the numbers increase. In the video, it is mentioned in relation to the aesthetic principles used by the ancient Greeks, such as in sculpture, and is also associated with the proportions found in natural structures like the spirals of sunflower seeds.
๐Ÿ’กPhi
Phi is the Greek letter used to represent the Golden Ratio. It is a mathematical concept that has been associated with beauty and perfection in art and nature. In the video, Phi is discussed as a ratio that appears in the proportions of various natural forms and was historically used by the ancient Greeks to represent physical perfection in their sculptures.
๐Ÿ’กGolden Rectangle
A Golden Rectangle is a rectangle whose sides are in the proportion of the Golden Ratio. It is a geometric figure that, when divided, can be used to create a series of squares based on Fibonacci numbers. In the video, the Golden Rectangle is shown to be related to the natural spirals observed in plants and seashells, illustrating the harmony between mathematics and the organic forms found in the natural world.
๐Ÿ’กLiber Abaci
Liber Abaci is a book written by Leonardo of Pisa, also known as Fibonacci. The book is historically significant as it introduced the sequence that now bears Fibonacci's name to the Western world. In the video, it is mentioned as the source of the Fibonacci Sequence and its connection to the spread of Arabic numerals in Europe.
๐Ÿ’กLeonardo of Pisa
Leonardo of Pisa, also known as Fibonacci, was an Italian mathematician who is best known for his work 'Liber Abaci', where he introduced the Fibonacci Sequence and Arabic numerals to Europe. In the video, he is credited with bringing these mathematical concepts to the Western world, which had a profound impact on the development of mathematics and numeracy.
๐Ÿ’กEfficiency in Nature
The concept of efficiency in nature refers to the way organisms and natural structures optimize their form and function for survival and reproduction. In the video, it is mentioned that the Fibonacci Sequence is observed in the arrangement of seeds in plants because it is the most efficient way to pack seeds into a small space, demonstrating how mathematical principles can explain natural phenomena.
๐Ÿ’กMathematics in Nature
The video explores how mathematics is not just a human invention but is also inherent in the natural world. It discusses how specific mathematical patterns, such as the Fibonacci Sequence and the Golden Ratio, are found in various natural structures like plants, flowers, and seashells. This concept highlights the universality of mathematical principles and their role in shaping the natural world.
๐Ÿ’กVi Hart
Vi Hart is a mathematical artist and educator known for her engaging and creative approach to explaining mathematical concepts. In the video, her video is referenced as a resource for understanding why the Fibonacci Sequence is an efficient pattern for seed arrangement in plants. Her work is an example of how mathematics can be presented in an accessible and visually appealing way.
๐Ÿ’กRoman Numerals
Roman numerals are a numeral system that originated in ancient Rome and were used throughout the Roman Empire. In the video, it is humorously mentioned that without Fibonacci's introduction of Arabic numerals to Europe, people would still be using Roman numerals, which are less efficient and more complex for mathematical operations.
๐Ÿ’กAesthetics in Art
Aesthetics in art refers to the principles of beauty and the appreciation of sensory stimulation. The video discusses how the Golden Ratio, or Phi, was used by the ancient Greeks to achieve a sense of physical perfection in their sculptures. This concept ties into the broader theme of the video, which is the intersection of mathematics and beauty in both the natural and human-made worlds.
Highlights

Mathematics is a natural invention, not created to harass English majors, and is found everywhere in nature.

The Fibonacci Sequence is a set of numbers found frequently in nature, starting with 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

Each number in the Fibonacci Sequence is the sum of the two preceding ones.

The Fibonacci Sequence was first described by Indian mathematicians around 1300 years ago and introduced to the West by Leonardo of Pisa in 1202.

Leonardo of Pisa, also known as Fibonacci, introduced Arabic numerals to Europe.

Fibonacci's book, Liber Abaci, used a thought experiment involving bunnies to describe the sequence.

The Fibonacci Sequence is easily observable in the natural world, particularly in plants.

The number of sections in a banana or petals on a flower often correspond to Fibonacci numbers.

The arrangement of seeds in sunflowers and pine cones follows Fibonacci numbers for efficient packing.

The Golden Ratio, approximately 1.618..., is derived from the ratio of consecutive Fibonacci numbers.

The Golden Ratio was known to the Greeks as Phi and was associated with physical perfection.

The Golden Rectangle, with sides in the ratio of successive Fibonacci numbers, can be divided into squares with Fibonacci lengths.

Drawing arcs from corner to corner of these squares forms spirals similar to those found in nature.

The Golden Rectangle and its spirals are observed in natural phenomena such as succulent leaves, pine cone lobes, and snail shells.

The beauty of mathematics is evident in its natural patterns and its application in understanding the world around us.

For further exploration of these concepts, Vi Hart's video is recommended and linked in the description.

The Fibonacci Sequence and the Golden Ratio are not only mathematical curiosities but also fundamental to efficient natural designs.

The video encourages viewers to engage with the content through comments on social media platforms or by subscribing to SciShow for more educational content.

Transcripts

Browse More Related Video

What is the Fibonacci Sequence & the Golden Ratio? Simple Explanation and Examples in Everyday Life

The Fibonacci Sequence and the Golden Ratio

Golden Ratio = Mind Blown!

The Golden Ratio: Is It Myth or Math?

The fabulous Fibonacci flower formula

Fibonacci = Pythagoras: Help save a beautiful discovery from oblivion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Fibonacci SequenceGolden RatioNature's PatternsMathematics in PlantsEfficient PackingPhi RatioAncient GreecePhysical PerfectionGolden RectangleNatural SpiralsSciShow EducationMathematical Beauty