The fabulous Fibonacci flower formula
TLDRThis Mathologer video delves into the fascinating presence of Fibonacci numbers in nature, particularly within the spiral patterns found in flower heads. The video offers a detailed explanation of why these numbers appear, emphasizing the mathematical core behind the phenomenon. Starting with the observation of spirals corresponding to Fibonacci numbers, the presenter outlines how plants grow from a central point, creating a pattern that leads to a dense packing of seeds or buds. The video also explores the connection between the visible spirals and the Fibonacci sequence, demonstrating through a unique proof that the sum of two consecutive Fibonacci numbers equals the next number in the sequence. Additionally, it addresses the prevalence of the Fibonacci sequence despite other sequences, such as double Fibonacci numbers and Lucas numbers, also following the same growth rule. The video concludes with a promise of a follow-up focusing on the golden ratio's relation to the topic.
Takeaways
- 🌿 Fibonacci numbers commonly appear in nature, especially visible in flower heads, pine cones, and pineapples.
- 🔍 The video provides an accessible explanation aimed at uncovering the mathematical principles that result in Fibonacci numbers in nature.
- 🌀 Observations of flower heads reveal visible spiral patterns, which consist of different Fibonacci numbers depending on the section of the flower observed.
- 🌱 The video illustrates how plants grow from a central point, pushing outwards and forming homogeneous patterns that are mathematically predictable.
- 📏 The arrangement and growth of buds in plants display a robust pattern that maintains a consistent appearance over time, regardless of perspective changes.
- 🔢 The video explains a mathematical rule where two sets of spirals (green and red) always add up to a third (blue), following the pattern of Fibonacci sequence growth.
- 🎨 The creator of the video offers a unique proof of this pattern, demonstrating the interplay between these spirals through visual aids.
- 🌼 Besides Fibonacci numbers, other numerical sequences like Lucas numbers also emerge in natural patterns, suggesting a broader rule at play.
- 🧐 The video suggests that the predominance of Fibonacci sequences in nature might be explained by their rapid establishment and visibility in the early stages of plant growth.
- 📚 For more detailed mathematical connections, particularly with the golden ratio, viewers are encouraged to watch a follow-up video.
Q & A
Why are Fibonacci numbers found in nature, particularly in the arrangement of flower heads?
-Fibonacci numbers appear in nature due to the way plants grow from a central point, pushing out new buds which naturally form spirals. These spirals often correspond to the numbers in the Fibonacci sequence, which is a series where each number is the sum of the two preceding ones.
What is the significance of the spirals in the arrangement of seeds or buds in a flower head?
-The spirals are significant because they represent an efficient packing pattern that allows for the densest possible arrangement of seeds or buds. This pattern emerges naturally as the plant grows from a central point, with new growth pushing outwards.
How does the growth pattern of plants relate to the Fibonacci sequence?
-The growth pattern of plants relates to the Fibonacci sequence because the number of spirals in one direction plus the number of spirals in the opposite direction always equals the number of spirals in the diagonal direction. This is analogous to the way the Fibonacci sequence progresses, where each number is the sum of the two preceding numbers.
What is the golden ratio (φ), and how is it connected to the Fibonacci sequence?
-The golden ratio, often denoted by the Greek letter φ (phi), is a mathematical constant approximately equal to 1.618. It is connected to the Fibonacci sequence because as the sequence progresses, the ratio of two consecutive Fibonacci numbers tends to converge to φ.
Why do some plants exhibit double the Fibonacci numbers or Lucas numbers in their growth patterns?
-Plants may exhibit variations such as double the Fibonacci numbers or Lucas numbers due to slight differences in their growth mechanisms or environmental factors. However, all these variations still adhere to the rule that two numbers in the sequence sum up to give the next number in the sequence.
What is the mathematical proof provided in the video that the number of green spirals plus the number of red spirals equals the number of blue spirals?
-The proof involves creating a closed path (yellow path) by alternating between green and red spirals. By marking points of intersection on this path with either green or red, it's shown that the number of green points equals the number of green spirals, the number of red points equals the number of red spirals, and the total number of points equals the number of blue spirals, thus proving that green plus red is equal to blue.
How does the plant's growth from a central point influence the appearance of Fibonacci numbers in its structure?
-The plant's growth from a central point results in a pattern where new buds or seeds are pushed out radially, creating a spiral pattern. This growth pattern naturally leads to the formation of spirals that correspond to consecutive Fibonacci numbers, as each new layer of growth adds to the previous ones in a way that follows the Fibonacci sequence.
What is the significance of the overlapping regions where consecutive Fibonacci numbers are visible in a plant's structure?
-The overlapping regions signify a continuous growth pattern where each new layer of growth contributes to the overall spiral pattern. This overlap allows for the efficient use of space and ensures that each seed or bud has the same role within the flower head, contributing to the plant's overall structure and function.
Why do the numbers in the Fibonacci sequence start with 1 and 1, or 1 and 2, and not some other numbers?
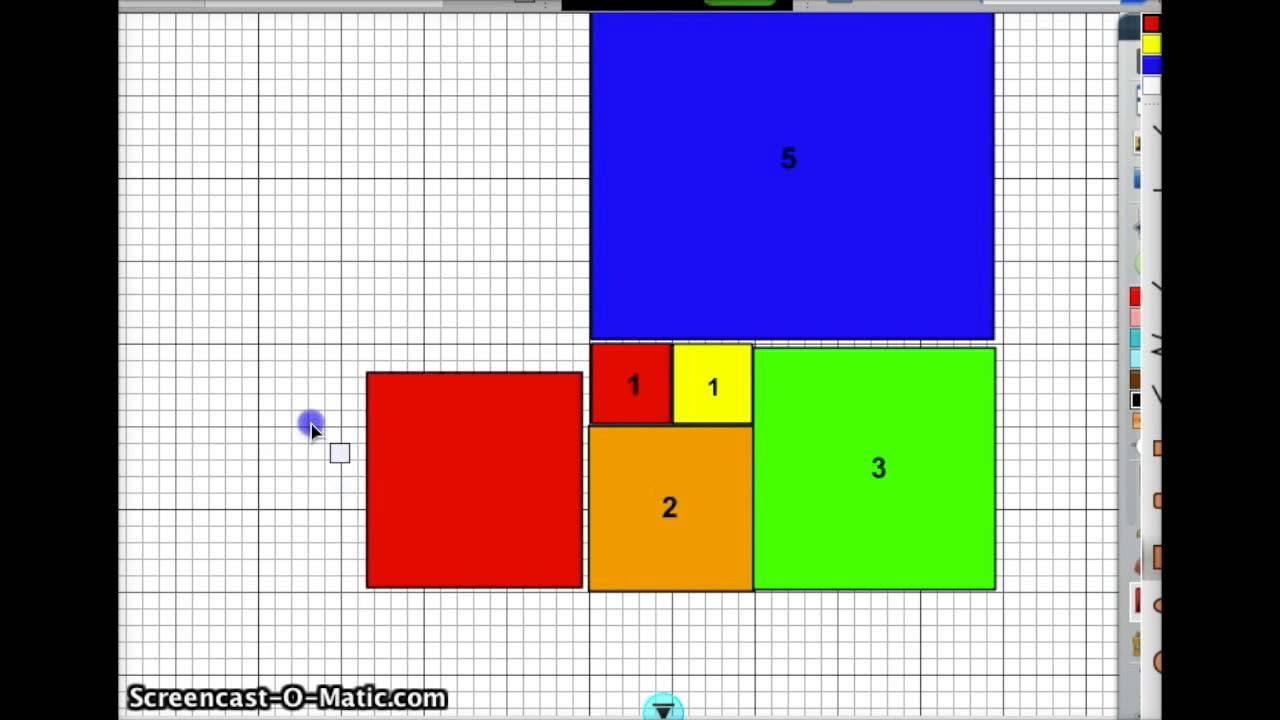
-The sequence typically starts with 1 and 1, or 1 and 2, because these are the smallest numbers that can initiate the pattern of each number being the sum of the two preceding ones. The specific starting numbers can vary, but the pattern of growth and the rule that two numbers sum up to the next one in the sequence remain consistent.
How does the arrangement of seeds or buds in a flower head contribute to the plant's reproductive success?
-The arrangement of seeds or buds in a flower head allows for maximum exposure to pollinators and optimizes the use of space, ensuring that each seed or bud has the best chance of survival and reproduction. The Fibonacci spiral pattern also allows for even distribution of resources and light, further contributing to the plant's reproductive success.
What are the implications of the Fibonacci sequence and golden ratio in understanding the design principles found in nature?
-The presence of the Fibonacci sequence and the golden ratio in natural structures suggests that these mathematical principles are fundamental to efficient growth and design in nature. Understanding these principles can provide insights into various fields, from architecture and art to computer science and robotics, where mimicking natural designs can lead to more efficient and aesthetically pleasing solutions.
Outlines
🌼 Fibonacci Numbers in Nature's Flower Heads
The video begins with an introduction to Fibonacci numbers and their prevalence in nature, particularly within the spirals of flower heads. The presenter, Mathologer, shares his quest to find a mathematical explanation for this phenomenon. He notes the presence of Fibonacci numbers such as 55, 34, 21, and 13 in the spirals and emphasizes their visibility in different regions of the flower head, always overlapping. The growth pattern of these plants, starting from a central point, is highlighted, with the sequence of Fibonacci numbers illustrated through the addition of consecutive numbers (1+1=2, 1+2=3, etc.). The video promises further exploration of related mathematical concepts, including the golden ratio, in a subsequent part.
🔢 The Mathematical Pattern of Spirals in Plants
This paragraph delves into the mathematical reasoning behind the appearance of Fibonacci numbers in the spiral arrangements of plants. The presenter discusses the growth of plants from a central point, leading to a homogeneous flower head. He describes the process of how each new bud or seed is pushed out radially, following straight lines, and how the flower head maintains a consistent pattern regardless of the viewing angle. The dense packing of the buds is also explored, with an optimal packing pattern that closely resembles the observed spirals. The video provides a visual demonstration of how two families of spirals can create a third, diagonal family, which is key to understanding the mathematical core of Fibonacci numbers' appearance in nature. The presenter teases his own proof of this phenomenon, which he promises to deliver later in the video.
📐 Proof of Fibonacci Sequence in Plant Spirals
The final paragraph presents a visual proof of the relationship between the spirals and the Fibonacci sequence. The presenter demonstrates how the number of spirals in two families (green and red) always adds up to the number of spirals in the third, diagonal family (blue). This is shown through a method of tracing a closed path around the spirals and highlighting points of intersection, which correspond to the spirals of each family. The proof concludes by showing that the number of green and red points equals the number of blue points, visually confirming that the sum of the two initial Fibonacci numbers (green and red) results in the next number in the sequence (blue). The video ends with a teaser for a future part that will explore the connection with the golden ratio.
Mindmap
Keywords
💡Fibonacci Numbers
💡Golden Ratio (φ)
💡Spiral
💡Central Point Growth
💡Seeds or Buds
💡Dense Packing
💡Diagonal Spirals
💡Lucas Numbers
💡Optimal Packing
💡Proof
💡Flower Head
Highlights
Fibonacci Numbers are found in nature, particularly in the arrangement of flower heads, pineapples, and pine cones.
The video attempts to provide an accessible explanation for why Fibonacci Numbers appear in nature.
Flower heads exhibit spirals that correspond to Fibonacci Numbers, such as 55, 34, 21, and 13.
Fibonacci sequence starts with two seeds, 1 and 1, and follows a pattern of addition (1+1=2, 1+2=3, etc.).
Plants that exhibit Fibonacci spirals grow from a central point, pushing out buds to form a homogeneous flower head.
The growth pattern of these plants leads to a stable arrangement where each seed or bud plays the same role within the flower head.
The radial growth of buds results in straight-line movement and a densely packed flower head.
The densest packing of circle-like objects approaches a pattern where layers interleave and circles align in certain ways.
The pattern of spirals in plants can be observed in any part of the plant, fitting the established mathematical model.
Two families of spirals create diamond-shaped cells, and a third type of spiral (diagonal spirals) cuts through these diamonds.
The mathematical core reason for Fibonacci numbers appearing in flower heads is that the sum of two spiral counts equals the third.
The video provides a visual proof that the number of green spirals plus the number of red spirals equals the number of blue spirals.
The appearance of Fibonacci numbers in nature may start with small seed numbers and grow according to a pattern established by the plant's growth.
Other sequences, such as double Fibonacci numbers and Lucas Numbers, also follow the rule of two numbers summing to the next in the sequence.
The predominance of the Fibonacci sequence may be due to detailed growth patterns and analysis specific to individual plants.
The video concludes with a proof that visually demonstrates the relationship between the counts of different colored spirals.
A second part of the video is promised to explore the connection with the golden ratio (φ).
Transcripts
Browse More Related Video

What is the Fibonacci Sequence & the Golden Ratio? Simple Explanation and Examples in Everyday Life

The Fibonacci Sequence: Nature's Code
The Fibonacci Sequence and the Golden Ratio

Fibonacci = Pythagoras: Help save a beautiful discovery from oblivion
Fibonacci Tutorial

Ch. 12.1 Sequences and Summation Notation
5.0 / 5 (0 votes)
Thanks for rating: