Related Rate Problem # 2 - Aircraft Converging

Sun Surfer Math

31 Mar 202208:18

EducationalLearning

32 Likes 10 Comments

TLDRThe video presents a rate problem involving two airplanes, a Cessna 208 heading north at 143 knots and a Lear 35 approaching Sedona Airport from the west at 410 knots. The problem requires understanding the geometry of the situation and applying the Pythagorean theorem to find the unknown distance between the two planes when the Cessna is 80 nautical miles from the airport and they are 261 nautical miles apart. By calculating the rate of change of this distance over time, the video demonstrates how to find the rate at which the two planes are closing the gap between them, which is determined to be 434.09 nautical miles per hour.

Takeaways

📐 **Right Triangle Setup**: The problem involves a right triangle formed by the paths of two airplanes, a Cessna 208 and a Lear 35, with the Sedona airport at the vertex.
✈️ **Cessna's Position and Speed**: The Cessna 208 is heading north at 143 knots and is 80 nautical miles from the airport.
🚀 **Lear's Position and Speed**: The Lear 35 is approaching the airport from the west at 410 knots.
📍 **Distance Between Airplanes**: At the given moment, the two airplanes are 261 nautical miles apart.
🧮 **Pythagorean Theorem Application**: The Pythagorean theorem is used to relate the distances (x and y) and the hypotenuse (d=261) of the right triangle.
🔍 **Finding Unknown Distance (x)**: The distance x is found using the Pythagorean theorem with the known values of y (80 miles) and d (261 miles), resulting in x ≈ 248.43 miles.
📉 **Rate of Change of Distance (dd/dt)**: The goal is to find the rate at which the distance between the two airplanes is changing over time (dd/dt).
🔢 **Derivative of the Pythagorean Equation**: The derivative of the Pythagorean theorem equation with respect to time is used to express dd/dt in terms of dx/dt and dy/dt.
📌 **Substitution of Known Values**: The known rates of change (dx/dt = 410, dy/dt = 143) and distances (x, y, d) are substituted into the derivative equation to solve for dd/dt.
🚨 **Result of dd/dt**: The calculated rate of change of the distance between the two airplanes with respect to time is 434.09 nautical miles per hour.
⏱️ **Timely Calculation**: The entire process is a snapshot in time, focusing on the instant when the Cessna is 80 nautical miles from the airport.

Q & A

What is the main topic of the video?
-The main topic of the video is solving a rate problem involving two airplanes, a Cessna 208 and a Lear 35, and calculating the rate at which their distance is changing.
What is the heading direction of the Cessna 208?
-The Cessna 208 is heading north.
What is the airspeed of the Cessna 208?
-The airspeed of the Cessna 208 is 143 knots.
In which direction is the Lear 35 heading?
-The Lear 35 is heading directly towards the Sedona airport from the west.
What is the airspeed of the Lear 35?
-The airspeed of the Lear 35 is 410 knots.
How far apart are the two airplanes when the Cessna 208 is 80 nautical miles from the airport?
-The two airplanes are 261 nautical miles apart.
What is the vertical distance from the airport to the Cessna 208, denoted as 'y' in the script?
-The vertical distance 'y' is 80 nautical miles.
What mathematical theorem is used to relate the distances in the problem?
-The Pythagorean theorem is used to relate the distances in the problem.
What does 'd' represent in the script?
-'d' represents the hypotenuse of the right triangle formed by the distances between the two airplanes and the airport.
What is the value of 'x' calculated using the Pythagorean theorem?
-The value of 'x' is calculated to be approximately 248.43 nautical miles.
What is the rate of change of the distance between the two airplanes with respect to time?
-The rate of change of the distance between the two airplanes with respect to time is 434.09 nautical miles per hour.
How does the video script guide the viewer to find the rate of change of distance?
-The video script guides the viewer to find the rate of change of distance by using the Pythagorean theorem to establish relationships between distances and their rates of change, and then differentiating that relationship to find the rate of change of the distance 'd' with respect to time.

Outlines

00:00

🛫 Introduction to the Airplane Rate Problem

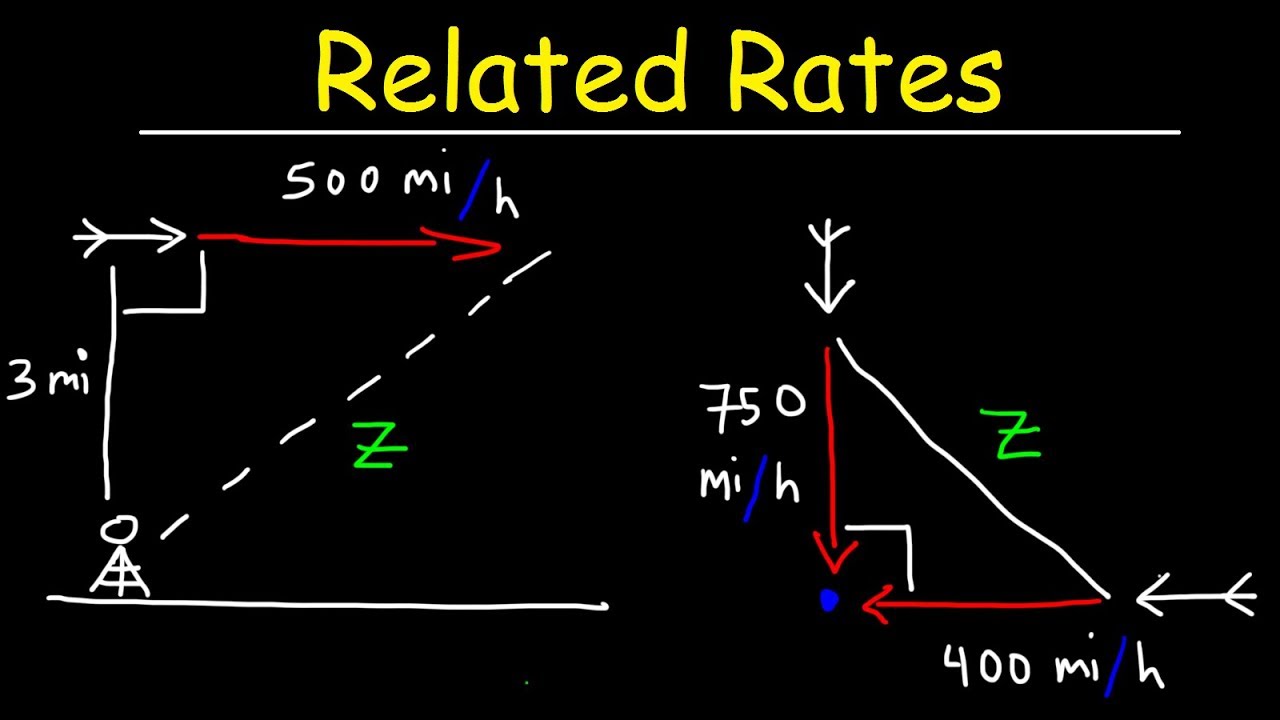
The video begins with the presenter introducing a related rate problem involving two airplanes, a Cessna 208 heading north at 143 knots and a Lear 35 heading towards the Sedona airport from the west at 410 knots. The presenter suggests drawing a diagram to visualize the situation and provides initial information about the positions and speeds of the airplanes. The Cessna is 80 nautical miles from the airport, and the two planes are 261 nautical miles apart. The presenter then introduces variables x and y to represent the unknown distances and uses the Pythagorean theorem to establish a relationship between these variables and the given distances. The goal is to find the rate at which the distance between the two airplanes is changing ("dd/dt"), for which the derivative of the Pythagorean theorem equation is used.

05:01

📐 Solving for the Rate of Change in Distance

The presenter continues by dividing the derivative of the Pythagorean theorem by the total distance (d) to simplify the equation for the rate of change of distance ("dd/dt"). This results in an equation where "dd/dt" is expressed as the sum of the products of the individual distances (x and y) divided by the total distance (d), and their respective rates of change ("dx/dt" and "dy/dt"). The presenter then substitutes the known values for "dx/dt", "dy/dt", and d into the equation. To find the unknown distance x, the presenter uses the Pythagorean theorem with the known values of y and d, yielding x as the square root of (261^2 - 80^2), which is approximately 248.43 nautical miles. With all values known, the presenter calculates the rate of change of distance with respect to time as 434.09 nautical miles per hour, indicating that this is how quickly the distance between the two airplanes is decreasing.

Mindmap

Keywords

💡Rate Problem

A rate problem is a mathematical challenge that involves calculating rates of change or motion, often in relation to distance, speed, or time. In the video, the rate problem involves two airplanes moving at different speeds and directions, and the goal is to determine how fast the distance between them is changing.

💡Cessna 208

The Cessna 208 is a type of aircraft mentioned in the video as one of the subjects in the rate problem. It is heading north at a speed of 143 knots. The Cessna's speed and direction are crucial to solving the problem, as they contribute to the overall motion and distance calculations.

💡Lear 35

The Lear 35 is another aircraft involved in the rate problem. It is heading directly towards the Sedona airport from the west at a speed of 410 knots. The Lear 35's movement is a key element in the problem, as it interacts with the Cessna 208's movement to determine the changing distance between the two planes.

💡Nautical Miles

Nautical miles are a unit of distance used in navigation and aviation. In the video, the distances between the airplanes and the airport are given in nautical miles, which is essential for calculating the relative positions and the rate at which the distance between the two planes is changing.

💡Pythagorean Theorem

The Pythagorean theorem is a fundamental principle in geometry that states the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. In the video, the theorem is used to relate the distances between the two airplanes, their respective speeds, and the rate at which the distance between them is changing.

💡Derivative

In calculus, a derivative represents the rate at which a function is changing at a certain point. In the context of the video, the derivative is used to find the rate of change of the distance between the two airplanes with respect to time, which is the central goal of the rate problem.

💡Distance Calculation

Distance calculation is the process of determining the spatial separation between two points. In the video, the distance calculation is central to solving the rate problem, as it involves finding the initial distances and then determining how these distances change over time.

💡Speed

Speed is a measure of how fast an object is moving, typically in terms of distance traveled per unit of time. In the video, the speeds of the Cessna 208 and the Lear 35 are given, and these values are essential for calculating the rate at which the distance between the two aircraft is changing.

💡Right Triangle

A right triangle is a triangle with one angle measuring 90 degrees. In the video, the relative positions of the two airplanes and the airport form a right triangle, which allows for the application of the Pythagorean theorem to solve for the unknown distances and the rate of change of those distances.

💡Radar

Radar is a system that uses radio waves to detect the position, speed, and other characteristics of objects. In the video, radar is mentioned as the source of the speed data for the Lear 35, which is crucial information for setting up and solving the rate problem.

💡Rate of Change

The rate of change is a term used to describe how quickly a quantity is changing over time. In the video, the main objective is to calculate the rate of change of the distance between the two airplanes with respect to time, which involves understanding their speeds and the geometry of their relative positions.

Highlights

The problem involves a rate problem related to the distance between two airplanes, a Cessna 208 and a Lear 35.

Drawing a diagram is suggested to visualize the problem effectively.

The Cessna 208 is heading north at 143 knots, and the Lear 35 is heading towards the Sedona airport from the west at 410 knots.

The Cessna is 80 nautical miles from the airport, and the two airplanes are 261 nautical miles apart.

The variables x and y are introduced to represent the distances from the airport and the horizontal distance between the planes, respectively.

The rate at which y changes is the airspeed of the Cessna, and dx/dt represents the rate at which the Lear is approaching from the west.

Three pieces of information are provided: the vertical distance y, the horizontal distance x, and the total distance d between the planes.

The Pythagorean theorem is applied to relate the distances x, y, and d in a right triangle.

The derivative of the Pythagorean theorem equation is used to find the rate of change of the distance between the planes.

The derivative equation is simplified to dd/dt = (x/d)(dx/dt) + (y/d)(dy/dt).

Substituting the known values for dx/dt, dy/dt, and d allows for solving for dd/dt.

The value of x is found using the Pythagorean theorem with the given values of y and d.

The calculated value for x is approximately 248.43 nautical miles.

The final expression for the rate of change of distance with respect to time is derived.

The rate of change of distance between the two airplanes with respect to time is calculated to be 434.09 nautical miles per hour.

This rate indicates how quickly the distance between the two planes is changing as they move towards each other.

The problem demonstrates the application of derivatives and the Pythagorean theorem in a real-world scenario involving air traffic.

The solution process involves careful substitution of known values and algebraic manipulation to find the desired rate of change.

Related Rate Problem # 2 - Aircraft Converging

Takeaways

Q & A

What is the main topic of the video?

What is the heading direction of the Cessna 208?

What is the airspeed of the Cessna 208?

In which direction is the Lear 35 heading?

What is the airspeed of the Lear 35?

How far apart are the two airplanes when the Cessna 208 is 80 nautical miles from the airport?

What is the vertical distance from the airport to the Cessna 208, denoted as 'y' in the script?

What mathematical theorem is used to relate the distances in the problem?

What does 'd' represent in the script?

What is the value of 'x' calculated using the Pythagorean theorem?

What is the rate of change of the distance between the two airplanes with respect to time?

How does the video script guide the viewer to find the rate of change of distance?