Related Rates - Airplane Problems
TLDRThe video script discusses two related rates problems involving airplanes. The first problem involves an airplane flying horizontally at 400 miles per hour, calculating the rate of change of the distance to a radar station when the plane is five miles away. The second problem involves two intersecting planes, one traveling west at 400 mph and the other south at 750 mph, determining the rate at which the distance between them is changing. Both problems are solved using the Pythagorean theorem and implicit differentiation, resulting in the rates of 320 mph and -850 mph, respectively.
Takeaways
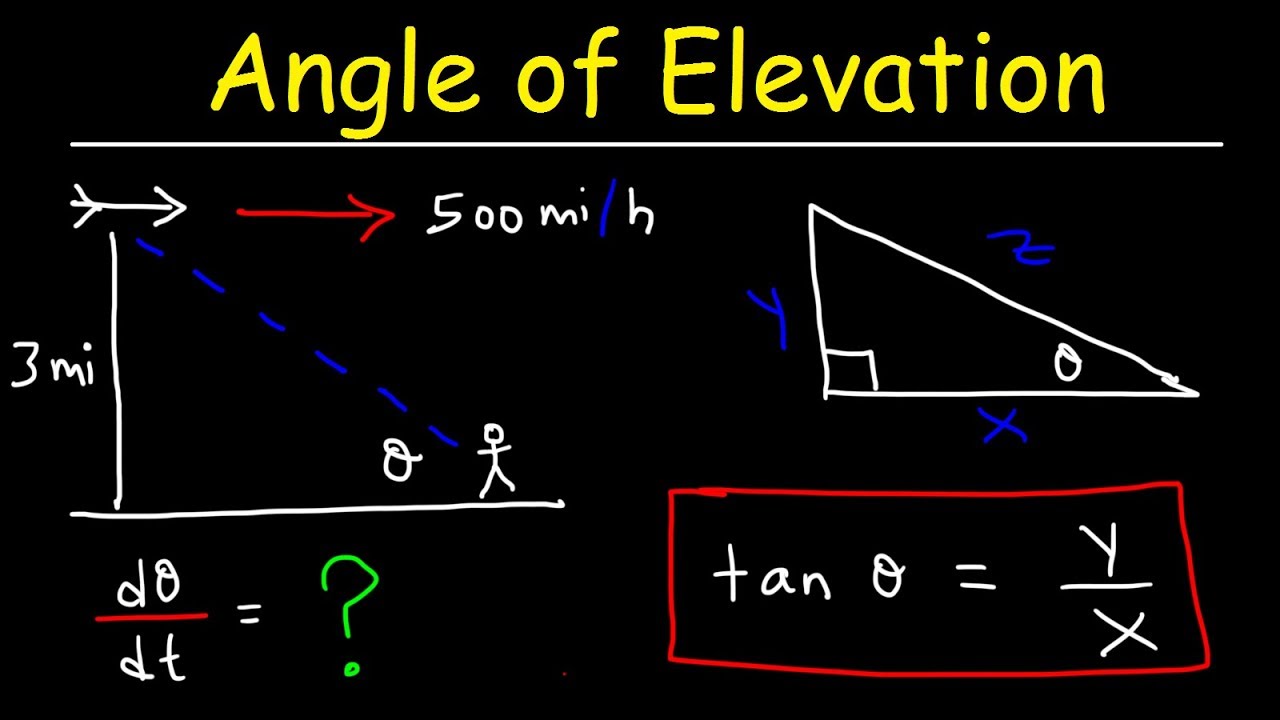
- 🛫 The airplane is flying horizontally at a speed of 400 miles per hour and an altitude of 3 miles above a radar station.
- 📐 The problem involves using related rates to find how fast the distance between the plane and the radar station is changing.
- 🎯 The goal is to calculate dz/dt when the plane is 5 miles away from the radar station, using the Pythagorean theorem (z^2 = x^2 + y^2).
- 🏁 At the point when the plane is 5 miles away (point B), y remains constant at 3 miles and dx/dt is 400 miles per hour.
- 🧠 Implicit differentiation is used to solve for dz/dt, with the formula 2z * dz/dt = 2x * dx/dt + 0 (since y is constant).
- 🔢 The calculation yields a dz/dt of 320 miles per hour, indicating the rate of change of the distance between the plane and the radar station.
- 🛫 Two airplanes are approaching a convergence point, with the first traveling west at 400 mph and the second traveling south at 750 mph.
- 📍 The first plane is 160 miles east and the second is 300 miles north of the convergence point, with dx/dt being -400 and dy/dt being -750.
- 🔄 Using the same Pythagorean approach, the distance z between the planes is found to be 340 miles before they start converging.
- 📊 Differentiating the equation with respect to time gives 2z * dz/dt = 2x * dx/dt + 2y * dy/dt, leading to a dz/dt of -850 miles per hour.
- 🔴 An alternative method using the formula dz/dt^2 = (dx/dt)^2 + (dy/dt)^2 also confirms the same result, with the negative sign indicating the planes are getting closer.
Q & A
What is the initial altitude of the airplane from the radar station?
-The initial altitude of the airplane from the radar station is three miles.
What is the horizontal speed at which the airplane is traveling?
-The airplane is traveling horizontally at a speed of 400 miles per hour.
What is the rate of change of the distance between the plane and the radar station when the plane is five miles away?
-The rate of change of the distance between the plane and the radar station when the plane is five miles away is 320 miles per hour.
How is the distance 'z' calculated in the first problem?
-The distance 'z' is calculated using the Pythagorean theorem where z squared is equal to x squared plus y squared. Given x is four and y is three, z is found to be the square root of (16 + 9) which is 4.
What is the formula used to find the rate of change of 'z' with respect to time in the first problem?
-The formula used to find the rate of change of 'z' with respect to time is dz/dt = (dx/dt * x + x * dx/dt) / z, which is derived from differentiating the equation z^2 = x^2 + y^2 with respect to time.
In the second problem, what are the speeds and directions of the two planes?
-In the second problem, the first plane is traveling west at 400 miles per hour and is 160 miles east from the convergence point. The second plane is traveling south at 750 miles per hour and is 300 miles north from the convergence point.
What is the rate of change of the distance between the two planes as they approach the convergence point?
-The rate of change of the distance between the two planes as they approach the convergence point is -850 miles per hour, indicating that the distance is decreasing at this rate.
How is the distance 'z' calculated in the second problem?
-The distance 'z' is calculated using the Pythagorean theorem where z squared is equal to x squared plus y squared. Given x is 160 and y is 300, z is found to be the square root of (160^2 + 300^2) which is 340.
What is the alternative method to find the rate of change of 'z' with respect to time in the second problem?
-The alternative method to find the rate of change of 'z' with respect to time is to use the formula dz/dt squared = (dx/dt) squared + (dy/dt) squared. The square root of this value gives the rate of change of 'z', which considering the context of the planes converging, should be negative.
How does the value of 'y' affect the calculation in the first problem?
-In the first problem, 'y' is a constant representing the altitude of the plane, and since it does not change, its rate of change dy/dt is 0. This means that the derivative of y squared in the equation is zero, simplifying the differentiation process.
What is the significance of the negative sign in the rate of change of 'z' in the second problem?
-The negative sign in the rate of change of 'z' in the second problem indicates that the distance between the two planes is decreasing as they approach the convergence point, which is consistent with the fact that they are moving towards each other.
What is the role of implicit differentiation in solving these problems?
-Implicit differentiation is used to find the rate of change of a variable with respect to time in problems where the relationship between variables is not explicitly given. It allows us to differentiate复合函数 with respect to time, which is crucial in calculating the rate of change of distances in these problems.
Outlines
🛫 Airplane Distance Calculation
This paragraph discusses a problem related to an airplane flying horizontally at a speed of 400 miles per hour, 3 miles above a radar station. The goal is to calculate the rate of change of the distance between the plane and the radar station when the plane is 5 miles away. The solution involves creating a right triangle with the plane's horizontal distance (x), vertical altitude (y), and the direct distance to the radar station (z). Using the Pythagorean theorem and implicit differentiation with respect to time, the problem is solved, resulting in a rate of change of distance (dz/dt) of 320 miles per hour.
🛩️ Convergence of Two Airplanes
The second paragraph presents a scenario where two airplanes are approaching a convergence point, with the first traveling west at 400 miles per hour, 160 miles east of the point, and the second traveling south at 750 miles per hour, 300 miles north of the point. The task is to find the rate at which the distance between the two planes is changing. By setting up a right triangle with x, y, and z representing the respective distances, and applying the Pythagorean theorem and implicit differentiation, the rate of change of distance (dz/dt) is calculated to be negative 850 miles per hour, indicating the planes are getting closer.
🚀 Alternative Method for Airplane Convergence
This paragraph introduces an alternative method to calculate the rate of convergence (dz/dt) for the two airplanes from the previous scenario. It reiterates that none of the variables x, y, and z are constants and applies the formula dz/dt squared equals dx/dt squared plus dy/dt squared. By squaring the given rates and adding them, the square root is taken to find the absolute value of dz/dt. The negative sign is then applied based on the context of the planes converging, confirming the previous result of a negative 850 miles per hour as the rate of change of distance between the two airplanes.
Mindmap
Keywords
💡Airplane
💡Related Rates
💡Horizontally
💡Altitude
💡Pythagorean Theorem
💡Implicit Differentiation
💡Convergence Point
💡Rate of Change
💡Right Triangle
💡Derivative
💡Speed
Highlights
An airplane is flying horizontally at a speed of 400 miles per hour.
The airplane is at an altitude of three miles above a radar station.
The goal is to calculate how fast the distance between the plane and the radar station is changing.
The plane will eventually be five miles away from the radar station at a certain point.
The altitude (y) of the plane remains constant at three miles, so dy/dt is 0.
The Pythagorean theorem is used to relate x, y, and z in the right triangle formed by the plane's position.
Implicit differentiation with respect to time is performed to find dz/dt.
The rate of change of the distance (dz/dt) between the plane and the radar station is found to be 320 miles per hour.
Two airplanes are about to intersect at a single point, with the first plane traveling west at 400 miles per hour and the second traveling south at 750 miles per hour.
The first plane is 160 miles east and the second plane is 300 miles north from the convergence point.
The rate at which the distance between the two planes is changing (dz/dt) is the goal of this problem.
The derivative of dz/dt is calculated using the equation 2z * dz/dt = 2x * dx/dt + 2y * dy/dt.
The value of dz/dt is found to be -850 miles per hour, indicating the planes are getting closer.
An alternative method to find dz/dt is presented, using the equation dz/dt^2 = (dx/dt)^2 + (dy/dt)^2.
The square root of the equation gives the magnitude of dz/dt, which is negative due to the converging nature of the planes.
The problem demonstrates the application of related rates in calculating the change in distance over time in real-world scenarios.
The use of right triangles and the Pythagorean theorem is crucial in solving these problems related to motion and distance.
Implicit differentiation is a key mathematical technique used to solve related rate problems involving multiple variables.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: