Math 11 - Section 4.4

Professor Monte

23 Apr 202035:47

EducationalLearning

32 Likes 10 Comments

TLDRThe video transcript focuses on three key properties of integrals in calculus. First, it explains how to add integrals together, demonstrating how to find the area under a curve between two points by breaking it down into smaller intervals if needed. Second, it covers finding the area between two curves by integrating the top curve and subtracting the integral of the bottom curve. The process is illustrated with an example involving a parabola and a line. Lastly, the transcript discusses calculating the average value of a function over an interval, which is done by integrating the function and dividing by the length of the interval. An application problem involving average monthly revenue is solved to show this in action. The summary concludes with an encouragement to practice these concepts and to ask questions for further clarification.

Takeaways

📚 The addition property of integrals allows us to split the integration of a continuous function over an interval into the sum of integrals over subintervals.
📈 When dealing with piecewise-defined functions, we can calculate the integral by integrating each piece separately and then summing the results.
🔢 To find the area between two curves, we integrate the top curve's function minus the bottom curve's function over the interval between their points of intersection.
✏️ When finding the area under a curve between two points, it's crucial to determine which curve is the top and which is the bottom to ensure the correct order of subtraction.
🤔 The average value of a function over an interval is found by integrating the function over the interval and then dividing by the length of the interval.
💡 The average value can be thought of as the total area under the curve divided by the width of the interval, which gives the average height.
📉 For problems involving accumulation, such as sales over time, we can model the situation with an integral and find quantities like average revenue.
🧮 It's essential to be careful with constants and exponents when performing integration, as they can significantly affect the result.
📐 Sketching the curves can be helpful in visualizing the problem and determining the order of the curves for area calculations.
🤓 Always check the result of an integration problem to ensure it makes sense in the context of the problem, such as ensuring the area is positive.
📝 When calculating the average value of a function, it's common to use the formula 1/(B-A) * ∫[f(x) dx] from A to B, where A and B are the interval limits.
💻 For practical applications, such as revenue calculations, it's important to understand whether the result represents a total or an average value over the given period.

Q & A

What is the first property of integrals discussed in the transcript?
-The first property discussed is the addition property of integrals, which allows for the addition of integrals together over a continuous function.
How does the addition property of integrals work when integrating between two points a and b with a value c between them?
-The addition property allows you to calculate the integral from a to b by breaking it down into the sum of the integral from a to c and the integral from c to b.
What is a piecewise-defined function?
-A piecewise-defined function is a function that is defined by multiple sub-functions, each applicable to a different interval or 'piece' of the domain.
How does one find the area under a piecewise-defined function over an interval?
-To find the area under a piecewise-defined function, you integrate each piece of the function over the respective sub-intervals that make up the total interval, and then sum these areas.
What is the process to find the area between two curves?
-To find the area between two curves, you first find the points of intersection of the curves. Then you integrate the top curve's function minus the bottom curve's function over the interval between these points of intersection.
How do you determine which curve is the top and which is the bottom when finding the area between two curves?
-You can determine which curve is on top by picking a test point within the interval of interest and evaluating both functions at that point. The function with the greater value at the test point corresponds to the top curve.
What is the formula to find the average value of a function over an interval [a, b]?
-The average value of a function over an interval [a, b] is given by (1/(b-a)) times the integral from a to b of the function f(x) with respect to x.
In the context of the transcript, what is the application of finding the average monthly revenue for a music manager's website?
-The application involves using the average value of a function to calculate the average monthly revenue attributable to the website over the first four months of sale.
How does the music manager's problem relate to the concept of accumulated sales?
-The music manager's problem is an example of accumulated sales where the revenue is modeled by an exponential function of time, and the goal is to find the average revenue over a certain period.
What is the significance of the integral in calculating the total revenue for the music manager's website?
-The integral is used to calculate the total revenue because it sums up the contributions of all infinitesimally small revenue amounts over the given time interval, which is a continuous process.
Why is it important to ensure that the answer for the area between curves or average value of a function is positive?
-It is important because area and average value are physical quantities that cannot be negative. A negative result would imply a mathematical error or a misinterpretation of which function is the top or bottom curve.

Outlines

00:00

🌟 Introduction to Definite Integral Properties

The video begins by introducing the properties of definite integrals, focusing on how integrals can be added together. The concept is explained using a continuous function and the idea of breaking the integral from 'A' to 'B' into two parts at a point 'C'. An example problem involving a piecewise-defined function is solved, demonstrating the application of the addition property of integrals.

05:01

📈 Calculating the Area Under a Curve

The second paragraph delves into calculating the area under a curve defined by a piecewise function. The process involves finding the antiderivative of the function and evaluating it over the given interval, taking into account the points where the function changes its definition. The calculation is shown step by step, including the simplification that occurs when evaluating at points where the function is not defined.

10:03

🤔 Troubleshooting an Incorrect Answer

The presenter discusses a discrepancy between their calculated answer and the one provided in the book. They re-evaluate their work, looking for mistakes in the calculations and the process of integrating the function. The paragraph highlights the importance of checking one's work and understanding the mathematical principles behind the calculations.

15:06

📉 Finding the Area Between Two Curves

The video moves on to explain how to find the area between two curves. The method involves integrating the top curve's function and subtracting the integral of the bottom curve's function over the interval between the points of intersection of the two curves. The process is illustrated with an example problem, emphasizing the need to determine which curve is above the other within the interval.

20:08

🔍 Determining Which Curve is on Top

This paragraph focuses on how to determine which of the two curves is the top curve when finding the area between them. The presenter explains a method to find the curves' points of intersection and then use a test value within the interval to determine which function represents the top curve. The importance of correctly identifying the top curve is emphasized to ensure the correct area calculation.

25:09

🧮 Integrating to Find the Area Between Curves

The presenter continues the discussion on finding the area between two curves by actually performing the integration. They show the process of integrating the difference of the two functions over the interval from the points of intersection. The calculation involves finding antiderivatives and evaluating them at the limits of integration, resulting in the area between the curves.

30:11

🎓 Application: Average Monthly Revenue

The video concludes with an application problem involving the calculation of the average monthly revenue from a website over the first four months. The presenter uses the concept of the average value of a function, which is found by integrating the revenue function over the time interval and dividing by the length of the interval. The problem is solved step by step, showing how to apply the concept of average value in a real-world context.

35:13

📚 Summary of Key Concepts

The final paragraph summarizes the key concepts covered in the section, which include adding integrals together, finding the area between two curves, and calculating the average value of a function. The presenter encourages viewers to practice these concepts using problems from the book and to ask questions if they have any. They also mention that these topics will be further discussed in the next live session.

Mindmap

Keywords

💡Definite Integrals

Definite integrals are a fundamental concept in calculus that represent the signed area under a curve between two points on the x-axis. In the video, the concept is introduced as a way to calculate the area under a curve defined by a function from one point to another, which is essential for understanding the properties discussed.

💡Addition Property

The addition property of integrals allows for the decomposition of an integral over an interval into the sum of integrals over subintervals. In the context of the video, this property is used to calculate the area under a curve by breaking it down into smaller sections, which simplifies the process of finding the total area.

💡Continuous Function

A continuous function is one that has no breaks, jumps, or gaps in its domain. The property of continuity is important when dealing with integrals, as it ensures that the function can be integrated over an interval without encountering discontinuities. The video emphasizes that the addition property holds for continuous functions.

💡Piecewise-Defined Function

A piecewise-defined function is a function that is defined by different expressions over different intervals. The video uses an example of such a function to demonstrate how to calculate the area under a curve when the function changes its form at a certain point within the interval of integration.

💡Area Between Curves

The concept of finding the area between two curves is introduced as a method to calculate the region enclosed by the curves. The video explains that this is done by integrating the upper curve and subtracting the integral of the lower curve over the same interval, which is crucial for finding the enclosed area.

💡Intersection Points

Intersection points are the x-values where two curves meet. To find the area between two curves, one must first determine these points, as they define the interval over which the integral is computed. The video demonstrates how to find these points by setting the two functions equal to each other and solving for x.

💡Average Value of a Function

The average value of a function over an interval is a concept used to find the mean or average height of the curve over that interval. The video explains that this is done by integrating the function over the interval and then dividing by the length of the interval, which provides a single value representing the central tendency of the function's values over the interval.

💡Antiderivatives

Antiderivatives, also known as indefinite integrals, are functions whose derivatives are equal to the original function. In the context of the video, antiderivatives are used to evaluate definite integrals by applying the fundamental theorem of calculus, which is essential for finding areas and average values.

💡Revenue Function

The revenue function is a specific type of function used to model the income or sales over time. In the video, a revenue function is given in the form of an exponential function, and the average monthly revenue is calculated using the concept of the average value of a function, which has practical applications in business and economics.

💡Integration by Substitution

Integration by substitution is a technique used to evaluate integrals that are the result of a chain rule application. Although not explicitly mentioned in the transcript, the process of finding antiderivatives and evaluating definite integrals often involves this technique, which is a fundamental skill in calculus.

💡Fundamental Theorem of Calculus

The fundamental theorem of calculus connects differentiation and integration, stating that the definite integral of a function can be found by finding the antiderivative of the function and subtracting the value of the antiderivative at the lower limit of integration from its value at the upper limit. This theorem is central to the calculation of areas and is implicitly used throughout the video.

Highlights

Introduction to the properties of definite integrals in section four, point four.

Explanation of the addition property of integrals, allowing for the summation of integrals over different intervals.

Demonstration of integrating a piecewise function over an interval using the addition property of integrals.

Integration of a function from negative 2 to 3 using the point C as the division point between two areas.

Use of the antiderivative to evaluate the definite integral and calculation of the area under the curve.

Solution of a problem involving a piecewise-defined function and the application of the integral addition property.

Method for finding the area between two curves by integrating the difference of the top and bottom curves.

Technique to determine which curve is on top by evaluating the functions at a point within the interval of integration.

Procedure for calculating the average value of a function over an interval by integrating and dividing by the interval length.

Application of the average value calculation to estimate the average monthly revenue from a website over four months.

Conversion of the calculated average revenue per month into thousands of dollars for practical interpretation.

Emphasis on the importance of checking the sign of the final integral result to ensure it represents a positive area.

Explanation of the process to find the points of intersection of two curves to determine the limits of integration.

Illustration of the concept of differentiable functions and the handling of points that are not differentiable.

Use of polynomial functions in integrals and the simplification that occurs when evaluating at zero.

The approach to approximate the final answer using a calculator and the conversion of the result into a mixed number or decimal approximation.

Clarification on the difference between the total revenue and the average revenue, specifically for the context of the problem.

Encouragement for students to practice the concepts covered and to ask questions for further clarification.

Transcripts

Browse More Related Video

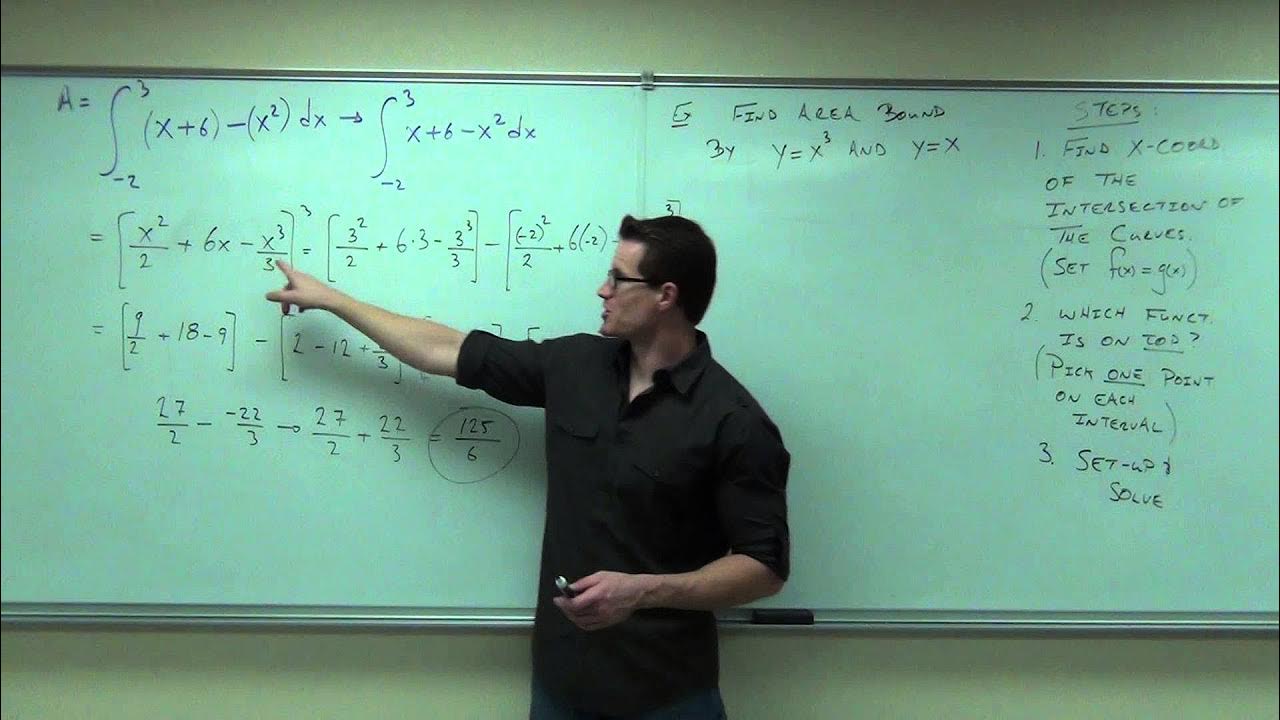
Calculus 1 Lecture 5.1: Finding Area Between Two Curves

An Intuitive Understanding of the Fundamental Theorem of Calculus

What does area have to do with slope? | Chapter 9, Essence of calculus

AP Calculus AB Crash Course Day 8 - Integration and Riemann Sums

Average Value of a Continuous Function on an Interval

Definite Integrals!

Related Tags

Integral Properties Definite Integrals Area Calculation Mathematical Analysis Piecewise Functions Curve Intersection Average Value Calculus Application Revenue Estimation Educational Content Problem Solving