Squeeze theorem (sandwich theorem) | Limits | Differential Calculus | Khan Academy
TLDRThe video script introduces the concept of the squeeze theorem, a fundamental tool in calculus, using a relatable everyday analogy. It explains how if a value is consistently greater than one value and less than another, and those two values become equal, the first value must also equal that common point. The script then sets the stage for using the squeeze theorem to prove a well-known limit in trigonometry, where the limit of sine of x over x as x approaches 0 is shown to equal 1, with the detailed proof to be presented in the next video.
Takeaways
- 👍 The video aims to prove that the limit as x approaches 0 of sine of x over x is equal to 1.
- 🤔 Before diving into the proof, the video introduces the concept of the squeeze theorem as a foundational element.
- 😎 The squeeze theorem is presented as the presenter's favorite mathematical theorem, highlighting its simplicity despite appearing complicated in textbooks.
- 📌 An everyday analogy involving calorie intake comparisons among three people (Sal, Umama, and Bill) is used to explain the squeeze theorem in an accessible manner.
- 📚 The mathematical formulation of the squeeze theorem is outlined: if a function is always greater than or equal to one function and less than or equal to another, and both these functions approach the same limit, then the original function also approaches that limit.
- 📈 A graphical representation is provided to visually demonstrate the squeeze theorem, showing how a function is 'squeezed' between two other functions that converge to the same limit.
- ✅ It's emphasized that the functions involved in the squeeze theorem do not necessarily need to be defined at the point of convergence for the theorem to apply.
- 💡 The video promises to utilize the squeeze theorem to prove the initial statement regarding the limit of sine of x over x as x approaches 0.
- 🏆 The practical usefulness of the squeeze theorem is to be showcased in a subsequent video, especially in proving limits related to trigonometric functions.
- ⏰ The video concludes with a teaser for the next installment where the actual application of the squeeze theorem in proving the initial claim will be discussed.
Q & A
What limit does the video aim to prove?
-The video aims to prove that the limit as x approaches 0 of sine of x over x is equal to 1.
What is the squeeze theorem?
-The squeeze theorem is a method in calculus that allows us to determine a limit by 'squeezing' a function between two other functions with known limits.
How does the video introduce the squeeze theorem?
-The video introduces the squeeze theorem with a relatable analogy of eating habits, comparing the caloric intake of the speaker (Sal), Umama, and a fictional character (Bill).
What is the mathematical representation of the squeeze theorem?
-Mathematically, the squeeze theorem states that if g(x) ≤ f(x) ≤ h(x) for some domain, and the limits as x approaches 'a' of g(x) and h(x) are both equal to some limit 'L', then the limit of f(x) as x approaches 'a' must also be 'L'.
Why is the squeeze theorem useful?
-The squeeze theorem is useful because it provides a way to evaluate limits of functions that may not be easily computed directly, by leveraging the limits of simpler functions that bound the function of interest.
How does the video relate the squeeze theorem to the limit of sine of x over x as x approaches 0?
-The video sets the stage for using the squeeze theorem to prove the limit of sine of x over x as x approaches 0, indicating that the theorem's application will be demonstrated in the next video.
What is the significance of the limit being proven in the context of trigonometric functions?
-The limit is significant because it is a fundamental concept in calculus, especially when dealing with derivatives of trigonometric functions.
How does the video emphasize the importance of understanding the squeeze theorem?
-The video emphasizes the importance of understanding the squeeze theorem by highlighting its practical applications and stating that it is a favorite theorem due to its intuitive nature and usefulness in solving complex problems.
What is the role of the example provided in the video?
-The example provided in the video serves to illustrate the concept of the squeeze theorem in a real-world context, making it easier for viewers to grasp the underlying principle.
What is the main takeaway from the video?
-The main takeaway from the video is an introduction to the squeeze theorem and its potential application in proving a specific limit involving trigonometric functions, with the detailed demonstration planned for the next video.
Outlines
📚 Introduction to the Squeeze Theorem
The video begins with the intention to prove that the limit of the sine function over x as x approaches 0 is equal to 1. However, before delving into trigonometry, the video introduces the concept of the squeeze theorem, which is a powerful tool in calculus. The theorem is explained through an everyday analogy involving calorie intake, demonstrating how if a person (Sal) always eats more than another (Umama) but less than a third person (Bill), and on a particular day (Tuesday), both Umama and Bill consume the same number of calories, Sal must also consume that same number of calories. This analogy is then translated into mathematical terms, where if g(x) ≤ f(x) ≤ h(x) for all x in some domain, and the limits of g(x) and h(x) as x approaches a are equal to L, then the limit of f(x) as x approaches a must also be L. The concept is further visualized through a graph, emphasizing that f(x) is bounded by g(x) and h(x), and thus its limit as x approaches a must be at the point where g(x) and h(x) coincide.
📈 Application of the Squeeze Theorem to a Trigonometric Limit
The video continues by discussing the application of the squeeze theorem to prove a specific trigonometric limit, namely that the limit of sine of x over x as x approaches 0 equals 1. The video emphasizes the practical utility of this limit in the context of taking derivatives of trigonometric functions. Although the actual proof is mentioned to be presented in the next video, the setup is laid out, indicating how the squeeze theorem will be instrumental in this proof. The video concludes by reinforcing the importance of understanding the squeeze theorem and its potential applications in calculus, leaving the audience eager to learn more in the subsequent video.
Mindmap
Keywords
💡limit
💡sine of x
💡approaches
💡squeeze theorem
💡trigonometry
💡derivative
💡domain
💡calories
💡math terms
💡graph
Highlights
The video aims to prove that the limit as x approaches 0 of sine of x over x is equal to 1.
Before delving into trigonometry, the video introduces another aspect of limits, the squeeze theorem.
The squeeze theorem is a favorite theorem in mathematics due to its intuitive nature.
The theorem is explained using an everyday scenario involving calorie intake to illustrate its concept.
The video emphasizes the usefulness of understanding the squeeze theorem for future calculus studies, particularly when taking derivatives of trigonometric functions.
The squeeze theorem states that if a function is always greater than one value and always less than another, and those two values are equal at some point, then the function must equal that point.
The theorem is formally introduced with the mathematical notation and conditions for its application.
A graphical representation of the squeeze theorem is provided to visually illustrate how the theorem works.
The video clarifies that the functions involved in the squeeze theorem do not necessarily have to be defined at the point of interest, as long as the limits exist.
The video concludes by stating that the squeeze theorem will be used in the next video to prove the limit of sine of x over x as x approaches 0.
The video highlights the practical application of the squeeze theorem in understanding and proving limits in calculus.
The video uses an informal, relatable approach to explain a complex mathematical concept, making it more accessible to viewers.
The video sets up anticipation for the next installment by promising to use the squeeze theorem in a practical application.
The video's approach to explaining the squeeze theorem emphasizes its significance and potential utility in mathematical analysis.
The video's use of a real-life analogy helps demystify the squeeze theorem, making it easier to understand for a broader audience.
The video's structure effectively builds from introducing the squeeze theorem to foreshadowing its application in the next segment.
The video concludes with a clear statement of intent for the next video, promising a practical demonstration of the squeeze theorem's utility.
Transcripts
Browse More Related Video

The Squeeze Theorem for Limits, Example 1
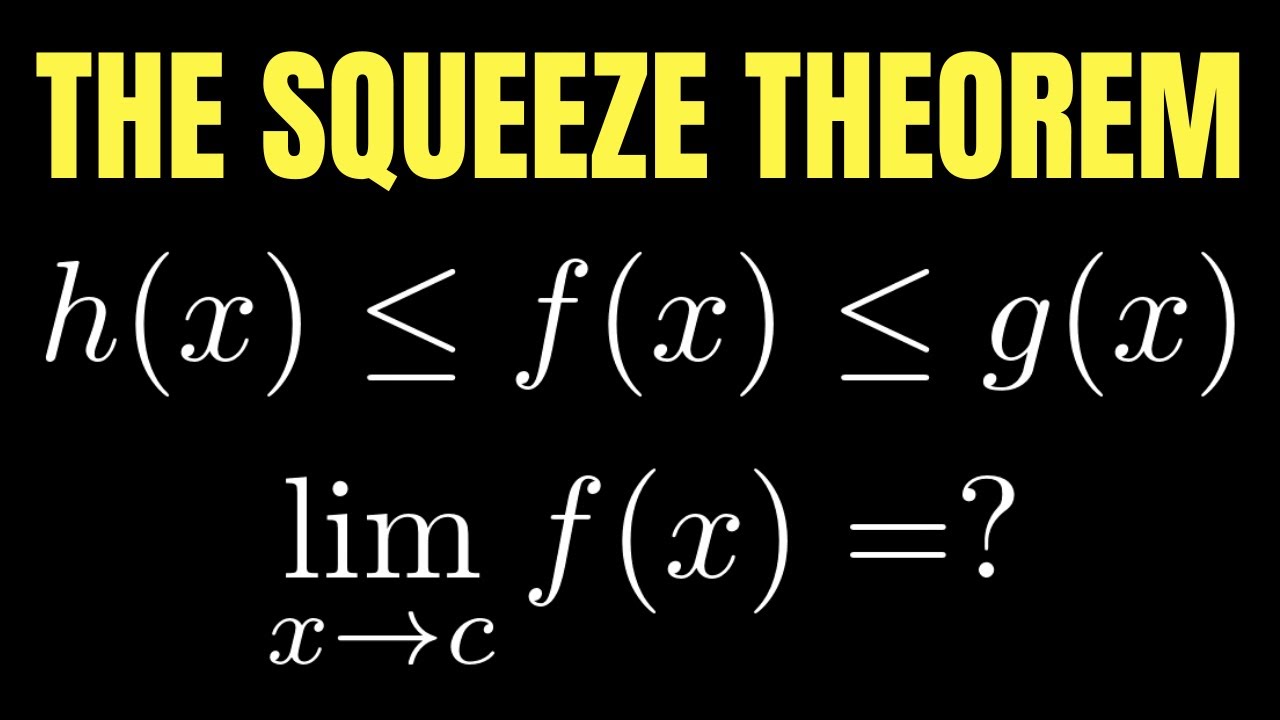
Calculus: The Squeeze Theorem Full Tutorial
Squeeze Theorem

Proof: lim (sin x)/x | Limits | Differential Calculus | Khan Academy
Limits of Oscillating Functions and the Squeeze Theorem

Squeeze theorem or sandwich theorem | Limits | Differential Calculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: