Area Between Two Curves-Curves that Cross
TLDRThe video script provides a comprehensive guide on calculating the area between two curves, particularly when the curves intersect. It outlines a step-by-step process for finding the area by dividing it into separate regions where one curve lies above the other. The method involves setting up integrals for each region, subtracting the lower curve from the upper, and then summing the areas to get the total. The script illustrates this with several examples, including those with linear, cubic, and parabolic curves, and demonstrates the use of anti-derivatives to solve the integrals. It also highlights the importance of determining the points where the curves intersect to accurately define the bounds of integration. The examples are solved meticulously, showcasing the mathematical process and the final results, which are the total areas between the curves.
Takeaways
- 📐 To find the area between two curves, first determine where the curves intersect and divide the region into separate areas if necessary.
- 🔍 Identify the bounds of integration (a to b) and determine which curve is above the other within each subinterval.
- ✅ For each subinterval, set up an integral where the top curve's function minus the bottom curve's function represents the area.
- 📈 Compute the integral for each subinterval separately to find the individual areas.
- 🔑 The total area between the curves is the sum of the individual areas (Area A + Area B, etc.).
- 🌀 In the first example, the area between f(x) = 6x and g(x) = x^3 - 3x from x = -1 to 2 is found by splitting the region into two parts at x = 0 and evaluating the respective integrals, resulting in a total area of 25.75 square units.
- 📉 For the second example with parabolas f(x) = x^2 - 2x + 1 and g(x) = -x^2, the region from 0 to 3 is split at x = 2, yielding areas of 6.67 and 3.667, respectively, for a total area of 10.34 square units.
- 🔺 In the third example, the area between the parabolas f(x) = -x^2 + 3x + 7 and g(x) = x^2 - 3x + 3 from -2 to 4 involves splitting the region at x = -1, resulting in areas of 5.67 and 41.67, respectively, for a total area of 47.34 square units.
- ⛔️ The fourth example with curves f(x) being a cubic and g(x) being a parabola over the interval from -2 to 4 requires finding three separate areas due to multiple intersections at x ≈ -0.813 and x ≈ 2.388, with the final total area being 54.77 square units.
- 🧮 The process involves finding antiderivatives and evaluating them at the bounds of integration to calculate the areas.
- 📋 It's important to accurately identify the curves' order and the bounds for each integral to ensure correct area calculations.
Q & A
What is the general approach to finding the area between two curves that intersect?
-The general approach involves identifying the points where the curves intersect and then calculating the area under each curve separately within the bounds of integration. The total area is the sum of these individual areas.
How do you determine the points where two curves intersect?
-You set the two functions equal to each other and solve for the points of intersection, which are the values of x where both functions yield the same y value.
What is the integral expression for the area between two curves when f(x) is above g(x)?
-The integral expression is ∫(f(x) - g(x)) dx, evaluated over the interval where f(x) is above g(x).
What is the integral expression for the area between two curves when g(x) is above f(x)?
-The integral expression is ∫(g(x) - f(x)) dx, evaluated over the interval where g(x) is above f(x).
In the first example, what are the functions f(x) and g(x)?
-In the first example, f(x) is 6x and g(x) is x^3 - 3x.
What are the bounds of integration for the first example?
-The bounds of integration for the first example are from x = -1 to x = 2.
How do you find the points where the curves in the first example intersect?
-You set 6x equal to x^3 - 3x and solve for x to find the points of intersection.
What is the total area between the curves in the first example?
-The total area between the curves in the first example is 25.75 square units.
In the second example, what are the functions f(x) and g(x)?
-In the second example, f(x) is x^2 - 2x + 1 (an upturning parabola) and g(x) is the same function but considered as a downturning parabola.
What is the method to calculate the area between two curves when they intersect more than once within the bounds of integration?
-When curves intersect more than once, you calculate the area in segments. You find each point of intersection and then compute the integral for the area between the curves over each segment separately, summing these areas to get the total area.
In the third example, what are the bounds of integration and what are the functions f(x) and g(x)?
-In the third example, the bounds of integration are from x = -2 to x = 4. The function f(x) is -x^2 + 3x + 7 (a downturning parabola), and g(x) is x^2 - 3x + 3 (an upturning parabola).
What is the total area between the curves in the third example?
-The total area between the curves in the third example is 47.34 square units.
In the final, more complicated example, how many areas are there between the curves?
-In the final example, there are three separate areas between the curves due to multiple points of intersection within the bounds of integration.
What is the total area between the curves in the final example?
-The total area between the curves in the final example is 54.77 square units.
Outlines
📐 Calculating the Area Between Two Curves
The video begins by explaining how to find the area between two curves when they intersect. It introduces the concept of splitting the area into two parts, Area A and Area B, based on which curve is above the other within the bounds of integration from point a to point b. The process involves calculating the integral of (f(x) - g(x)) for Area A and (g(x) - f(x)) for Area B, where f(x) is the red curve and g(x) is the blue curve. An example is provided with the curves f(x) = 6x and g(x) = x^3 - 3x, with the bounds from x = -1 to x = 2, showing how to find the area by integrating the respective functions over the intervals where each curve is above the other.
🔍 Finding the Area Between Upturning and Downturning Parabolas
The second problem focuses on finding the area between an upturning parabola (f(x) = x^2 - 2x + 1) and a downturning parabola (g(x)). The integration bounds are from x = 0 to x = 3. The video illustrates that the curves intersect within this interval, creating two separate areas. The area is calculated by integrating the difference of the functions over the respective intervals where one curve is above the other. The integral for Area A is simplified to ∫(x^3 - 12x)dx from -1 to 0, and for Area B, it is ∫(12x - x^3)dx from 0 to 2. The total area is the sum of both areas, resulting in 25.75 square units.
📉 Integrating Between a Downturning Parabola and a Linear Function
The third example deals with finding the area between a downturning parabola (f(x) = -x^2 + 3x + 7) and an upturning parabola (g(x) = x^2 - 3x + 3) over the interval from x = -2 to x = 4. The video explains that the curves switch positions at x = -1, creating two distinct areas. The area calculations involve integrating the difference of the functions over the intervals where one curve is above the other. The integral for Area A is ∫(2x^2 - 6x - 8)dx from -2 to -1, and for Area B, it is ∫(8 + 6x - 2x^2)dx from -1 to 4. The total area is found by summing the areas of A and B, yielding a total area of 47.34 square units.
🔢 Solving a More Complex Area Between Curves Problem
The fourth problem presents a more complex scenario with two curves, a downturning parabola and a cubic function, over the interval from x = -2 to x = 4. The curves intersect at three points, creating three separate areas. The video demonstrates how to calculate the area for each segment by integrating the difference of the functions. Area A is calculated from -2 to -0.813, Area B from -0.813 to 2.388, and Area C from 2.388 to 4. The integrals are solved using antiderivatives, and the areas are evaluated at the given bounds. The total area is obtained by summing the areas of A, B, and C, resulting in a total area of 54.77 square units.
🧮 Final Example: Area Between a Cubic and a Downturning Parabola
The final example in the video involves finding the area between a cubic function and a downturning parabola over the interval from x = -2 to x = 4. The curves intersect at two points, identified as -0.813 and 2.388. The area is divided into three parts: Area A from -2 to -0.813, Area B from -0.813 to 2.388, and Area C from 2.388 to 4. Each area is calculated by integrating the difference of the respective functions over the interval where one curve is above the other. The integrals are solved, and the areas are evaluated to find the total area, which sums up to 54.77 square units.
Mindmap
Keywords
💡Area between curves
💡Integration
💡Curves crossing
💡Anti-derivative
💡Definite integral
💡Parabolas
💡Cubic functions
💡Graphing
💡Desmos
💡Bounds of integration
💡Summation of areas
Highlights
The video explains how to find the area between two curves when they intersect, by dividing the region into separate areas and calculating the area of each.
For area A, where the top curve (f(x)) is above the bottom curve (g(x)), the integral is f(x) - g(x) from point a to c.
For area B, where the bottom curve (g(x)) is above the top curve (f(x)), the integral is g(x) - f(x) from point c to b.
The total area between the curves is the sum of areas A and B.
An example problem is solved where the area between f(x) = 6x and g(x) = x^3 - 3x is calculated from x = -1 to 2.
The area is divided into two parts: area A from -1 to 0 where g(x) is above f(x), and area B from 0 to 2 where f(x) is above g(x).
Area A is calculated as the integral from -1 to 0 of (x^3 - 3x) - 6x, which simplifies to x^4/4 - 12x^2.
Area B is calculated as the integral from 0 to 2 of 6x - x^3, which simplifies to 6x^2 - x^4/4.
The total area is found by evaluating the antiderivatives of the simplified integrals at the endpoints and summing the results: 5.75 + 20 = 25.75.
In another example, the area between the upturning parabola f(x) = x^2 - 2x + 1 and the downturning parabola g(x) = -x^2 + 2x + 1 is found from x = 0 to 3.
The area is divided into two parts: area A from 0 to 2 where g(x) is above f(x), and area B from 2 to 3 where f(x) is above g(x).
Area A is calculated as the integral from 0 to 2 of (5 - x^2) - (x^2 - 2x + 1), which simplifies to 4 + 2x - 2x^2.
Area B is calculated as the integral from 2 to 3 of (x^2 - 2x + 1) - (-x^2 + 2x + 1), which simplifies to 2x^2 - 2x - 4.
The total area is found by evaluating the antiderivatives at the endpoints and summing the results: 6.67 + 3.67 = 10.34.
In a third example, the area between the downturning parabola f(x) = -x^2 + 3x + 7 and the upturning parabola g(x) = x^2 - 3x + 3 is found from x = -2 to 4.
The area is divided into two parts: area A from -2 to -1 where g(x) is above f(x), and area B from -1 to 4 where f(x) is above g(x).
Area A is calculated as the integral from -2 to -1 of (x^2 - 3x + 3) - (-x^2 + 3x + 11), which simplifies to 2x^2 - 6x - 8.
Area B is calculated as the integral from -1 to 4 of (-x^2 + 3x + 11) - (x^2 - 3x + 3), which simplifies to 8 + 6x - 2x^2.
The total area is found by evaluating the antiderivatives at the endpoints and summing the results: 5.67 + 41.67 = 47.34.
In a more complex example with three separate areas, the points where the curves intersect are determined using a graphing tool like Desmos.
The areas are calculated by finding the appropriate integrals for each region, simplifying them, and evaluating the antiderivatives at the endpoints.
The total area is found by summing the areas of all three regions: 2.67 + 18.39 + 33.71 = 54.77.
Transcripts
Browse More Related Video
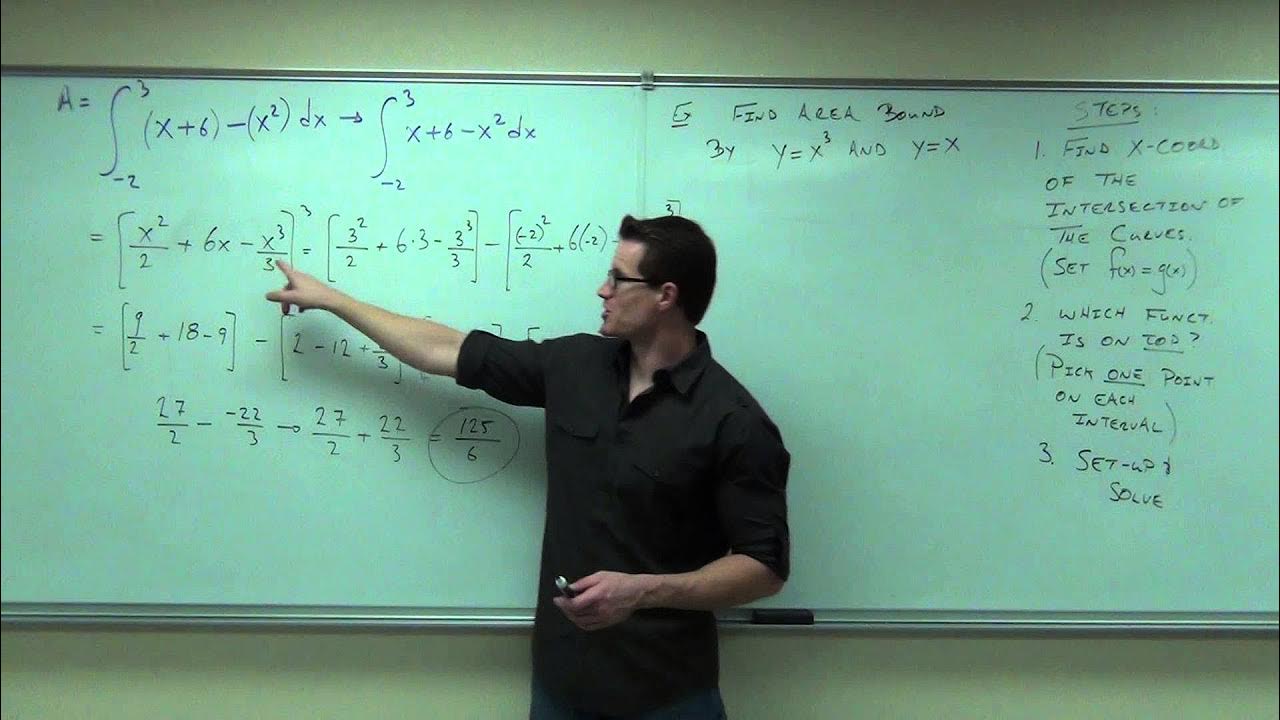
Calculus 1 Lecture 5.1: Finding Area Between Two Curves
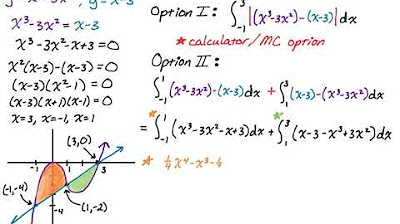
Area Between Two Curves with Multiple Regions: y = x^3-3x^2 and y = x-3
Area between curves | Applications of definite integrals | AP Calculus AB | Khan Academy

Washer method rotating around vertical line (not y-axis), part 1 | AP Calculus AB | Khan Academy

Finding The Area Under The Curve Using Definite Integrals - Calculus

Finding The Area Bounded By Three Curves Using Definite Integrals - Calculus
5.0 / 5 (0 votes)
Thanks for rating: