How to Find the Area of a Triangle with Trigonometry (Precalculus - Trigonometry 34)
TLDRThis video script offers an engaging exploration into the calculation of a triangle's area, simplifying the process for viewers. Traditionally, finding a triangle's area requires knowledge of the base and height. However, the script introduces a method that allows for area calculation without the height, given two sides and the included angle, or all three sides. This approach leverages the law of cosines and right triangle trigonometry, particularly the sine function, to deduce the height and subsequently the area. The script presents the formula for the area as one half times the product of two known sides and the sine of the angle between them. Additionally, it covers Heron's formula for calculating the area when all three sides are known, which involves summing the sides, finding the semi-perimeter (s), and using it in a square root function with the differences of s and each side. The video aims to make the often complex process of finding a triangle's area more accessible and straightforward.
Takeaways
- 📐 The area of a triangle can be found using the formula (1/2 * base * height).
- 🔍 If the triangle is not a right triangle and you don't know the height, you can still find the area if you know two sides and the included angle.
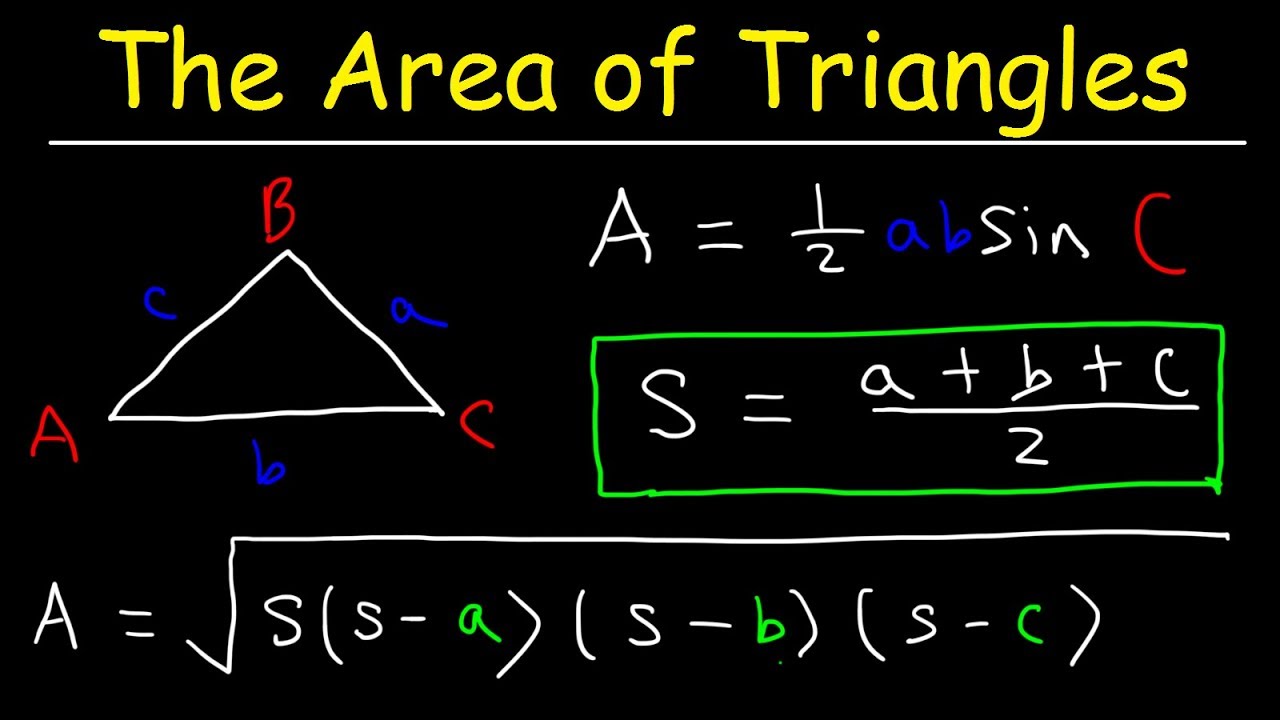
- 📐 The area formula for a triangle with two known sides and an angle is (1/2 * a * b * sin(C)), where a and b are the sides and C is the angle between them.
- 📐 For a right triangle, the height creates a right triangle, and the area can be found using trigonometric functions, specifically sine.
- 🔄 A substitution is used to replace the unknown height with a trigonometric expression, simplifying the area calculation.
- 📐 If all three sides of a triangle are known, Heron's formula can be used to find the area without knowing the height.
- 📐 Heron's formula involves calculating the semi-perimeter (s) of the triangle and then using it in a square root expression to find the area.
- 🔢 The semi-perimeter (s) is calculated as half the perimeter of the triangle, (s = 1/2 * (a + b + c)).
- 📐 The area using Heron's formula is given by (K = sqrt(s * (s - a) * (s - b) * (s - c))).
- 📐 Knowing two sides and the angle between (SAS) or all three sides (SSS) of a triangle allows for the application of the law of cosines, which is useful for area calculations.
- 🎓 Understanding the law of cosines and its relation to the area of a triangle is crucial for solving more complex geometry problems.
Q & A
What is the basic formula for calculating the area of a triangle?
-The basic formula for calculating the area of a triangle is one half times the base times the height (K = 1/2 * base * height).
If you know two sides and the angle between them in a triangle, how can you find the area without knowing the height?
-You can use the formula K = 1/2 * a * b * sin(C), where a and b are the two known sides, and C is the angle between them.
What is the Law of Cosines and how is it related to finding the area of a triangle without knowing the height?
-The Law of Cosines is a formula used in triangles to find a side length when given the lengths of the other two sides and the size of the angle between them. It's related to finding the area because if a triangle satisfies the Law of Cosines, you can find the area without explicitly knowing the height.
What is Heron's formula and how is it used to find the area of a triangle when all three sides are known?
-Heron's formula is a way to find the area of a triangle when you know the lengths of all three sides. You first calculate 's', which is the semi-perimeter of the triangle (s = 1/2 * (a + b + c)). Then you use the formula K = √(s * (s - a) * (s - b) * (s - c)) to find the area.
How does the process of doubling a triangle to form a rectangle help in finding the area of the triangle?
-Doubling the triangle forms a rectangle with the same base and height as the original triangle. Since the area of the rectangle is base times height, and this rectangle is composed of two identical triangles, dividing the area of the rectangle by two gives the area of one triangle.
What trigonometric function is used to relate the height of a triangle when you know two sides and the included angle?
-The sine function is used. Specifically, the height can be found using the formula height = a * sin(C), where 'a' is the hypotenuse of the right triangle formed by the height, and 'C' is the known angle.
What is the significance of the right triangle in the context of finding the area of a triangle without knowing the height?
-The right triangle is significant because it allows us to use trigonometric relationships to find the unknown height of the triangle. By knowing two sides and the angle between them, we can use the sine function to find the height, which then helps us calculate the area.
How does the substitution method simplify the process of finding the area of a triangle when the height is unknown?
-The substitution method simplifies the process by allowing us to replace the unknown height with an expression involving the known sides and the angle between them. This substitution leverages right triangle trigonometry to express the area in terms of known values, thus eliminating the need to find the height directly.
What is the concept behind the formula for finding the area of a triangle when two sides and the included angle are known?
-The concept is to use the known side lengths and the included angle to create a right triangle, where the height of the original triangle can be expressed in terms of the sides and angle. This allows the area to be calculated as half the product of the two known sides and the sine of the angle between them.
How does the area formula change when you know all three sides of a triangle?
-When you know all three sides, you use Heron's formula, which involves calculating the semi-perimeter 's' and then using the formula K = √(s * (s - a) * (s - b) * (s - c)) to find the area, where 'a', 'b', and 'c' are the side lengths of the triangle.
Why is it necessary to know the angle between two sides to apply the side-angle-side (SAS) formula for finding the area of a triangle?
-Knowing the angle between two sides is necessary because it allows the creation of a right triangle where the height of the original triangle can be related to the known sides via trigonometric functions, specifically the sine function, which is used to express the height in terms of the known side lengths and the angle.
Outlines
📐 Understanding Triangle Area Basics
This paragraph introduces the topic of finding the area of a triangle. It emphasizes that traditionally, one needs to know the base and height of the triangle. However, the video promises to simplify this process, especially for non-right triangles, by introducing methods that use two sides and the included angle or all three sides of the triangle, without explicitly knowing the height. It also hints at using the law of cosines and Heron's formula for these calculations.
🧮 Calculating Triangle Area Without Height
The second paragraph delves into how to calculate the area of a triangle when you know two sides and the angle between them, using trigonometric functions. It explains that the height of the triangle can be found using the sine of the known angle and the hypotenuse (which is one of the triangle's sides). The paragraph provides a formula for finding the area in this scenario, which is one half the product of two known sides and the sine of the angle between them. It also includes an example calculation using this method.
📐 Applying Heron's Formula for Unknown Sides
The third paragraph discusses Heron's formula, which is used to find the area of a triangle when all three sides are known. It outlines the steps to calculate 's', which is half the perimeter of the triangle, and then to use 's' in the formula to find the area. The paragraph provides a detailed example of how to apply Heron's formula, including the calculation of 's' and the subsequent steps to find the area.
🔢 Final Thoughts on Triangle Area Calculations
The final paragraph summarizes the methods presented in the video for finding the area of a triangle without knowing the height. It reiterates the two main approaches: using the sine of an angle when two sides and an angle are known, and using Heron's formula when all three sides are known. The paragraph concludes with an encouragement to practice these methods and hints at the next topic, harmonic motion, for a future video.
Mindmap
Keywords
💡Area of a Triangle
💡Base
💡Height
💡Right Triangle
💡Trigonometry
💡Law of Cosines
💡Heron's Formula
💡Sine Function
💡Semi-Perimeter (s)
💡Perimeter
Highlights
The video discusses an easier method to find the area of a triangle without knowing the height.
To find the area of a triangle, you traditionally need to know the base and the height.
The video introduces a method using two sides and an angle between them, or all three sides, to find the area.
The method involves a substitution that simplifies the area calculation using the law of cosines.
If the triangle satisfies the law of cosines, the area can be found without explicitly knowing the height.
The area of a triangle is traditionally calculated as one half times the base times the height.
The video explains how to use trigonometry to find the area when only two sides and the included angle are known.
The sine function is used to represent the relationship between the sides and the angle in a right triangle.
The height of the triangle can be found using the hypotenuse times the sine of the angle.
The area formula for a triangle with known sides and an angle is one half times the product of the sides times the sine of the angle.
Heron's formula is introduced for finding the area of a triangle when all three sides are known.
Heron's formula involves calculating 's', which is half the perimeter of the triangle, and then using it in a square root function.
The final area calculation with Heron's formula is the square root of 's' times 's' minus each side, multiplied together.
The video provides examples of calculating the area using both the side-angle-side method and Heron's formula.
The side-angle-side method is particularly useful when the triangle fits the law of cosines.
Heron's formula is a concise way to find the area of a triangle when all sides are known, without needing the height.
The video concludes by emphasizing the practicality of the methods introduced for finding the area of a triangle.
Transcripts
Browse More Related Video

How To Calculate The Height of a Triangle Using Heron's Formula
Area of an Oblique Triangle - SAS & SSS - Heron's Formula, Trigonometry

Related Rates - Area of a Triangle
Can you find the side lengths of the triangle? | (No Calculators!) |#math #maths #geometry

Special Right Triangles - 30 60 90 - Geometry & Trigonometry | SAT Math
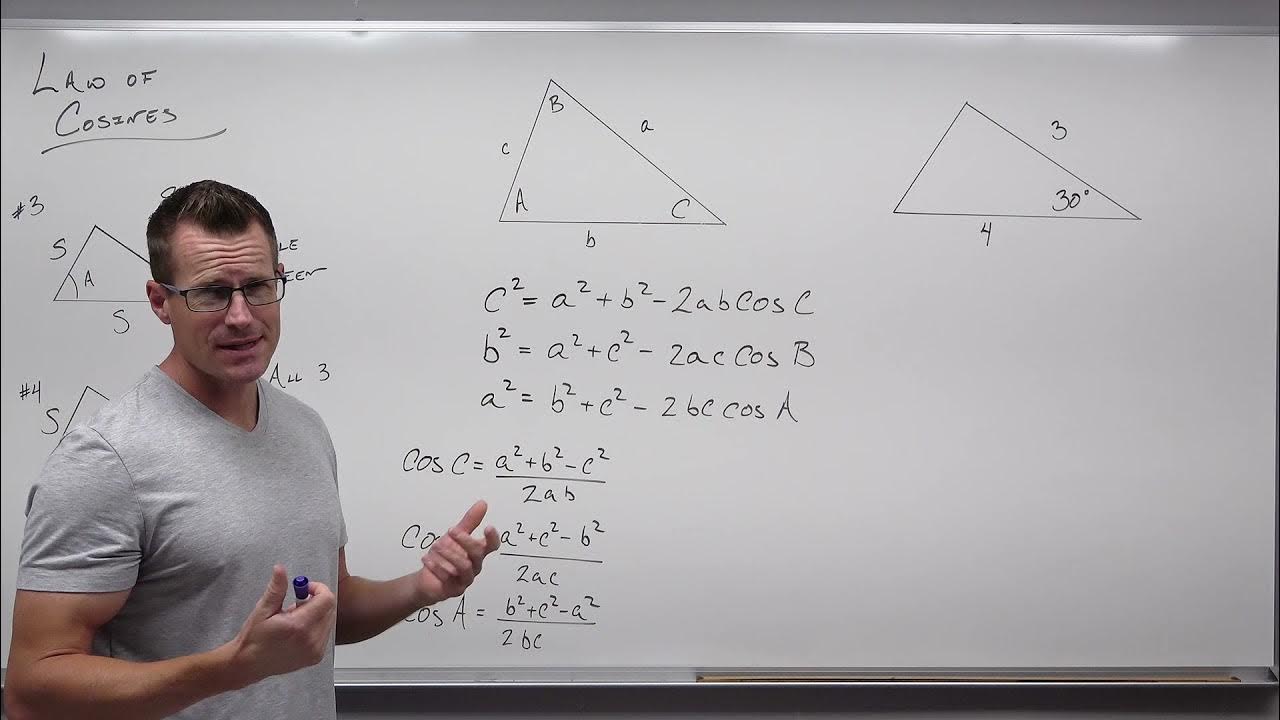
How to Use the Law of Cosines in Trigonometry (Precalculus - Trigonometry 33)
5.0 / 5 (0 votes)
Thanks for rating: