How To Calculate The Height of a Triangle Using Heron's Formula

The Organic Chemistry Tutor
13 Jun 202005:33
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video demonstrates how to calculate the height of a triangle when the lengths of all three sides are known. It introduces Heron's formula as the method to determine the triangle's area, using the semi-perimeter 's' and the sides a, b, and c. The video guides viewers through the calculation process step-by-step, from finding 's' to computing the area and finally deducing the height using the area and base. The example provided uses sides of lengths 9, 10, and 11, resulting in an area of 30 times the square root of 2, and a height of approximately 8.485 when converted to a decimal. The video concludes by emphasizing the utility of Heron's formula in such geometric calculations.

Takeaways
  • 📐 The video explains how to calculate the height of a triangle when the lengths of all three sides are known.
  • 📏 Huron's formula is used to calculate the area of a triangle when the lengths of all three sides are known.
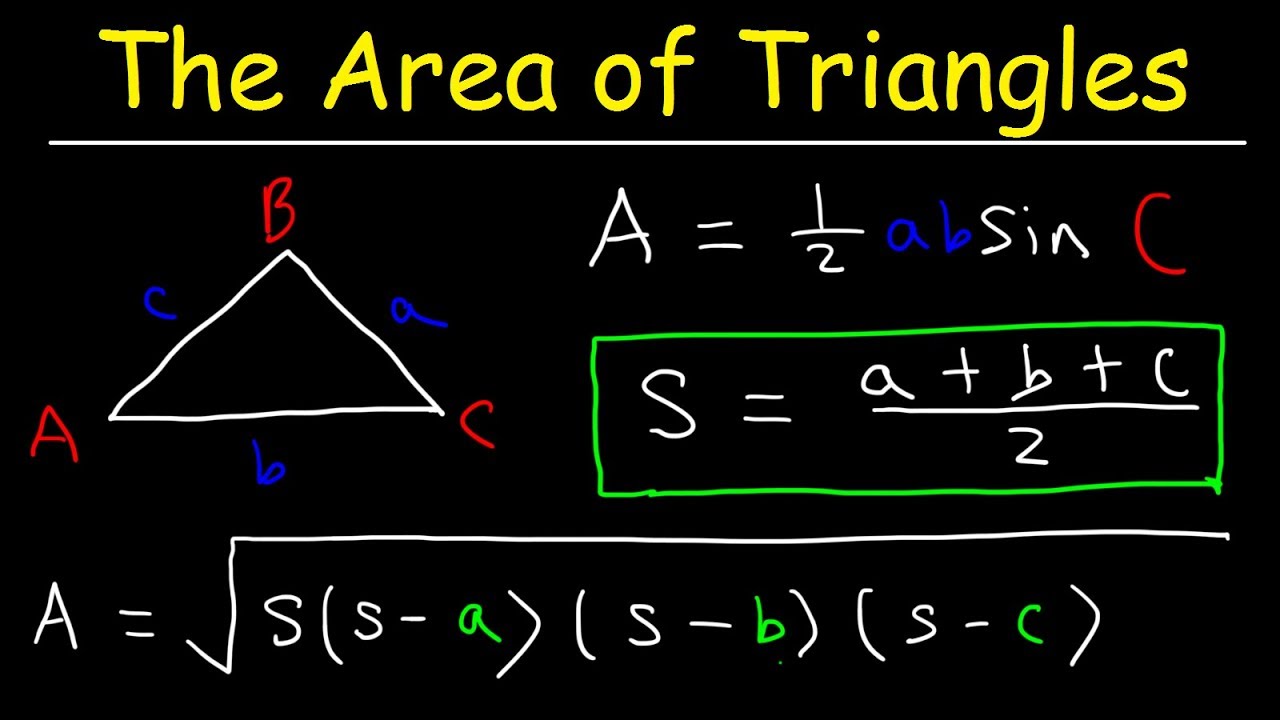
  • 🔢 The formula for 's' in Huron's formula is calculated as (a + b + c) / 2, where a, b, and c are the sides of the triangle.
  • 📉 The base of the triangle in the example is given as 10 units.
  • 📚 The sides of the example triangle are a = 9, b = 10, and c = 11.
  • 🧩 To find the area using Huron's formula, substitute the values of s, s-a, s-b, and s-c into the formula and calculate the square root.
  • 🔍 The area of the triangle is simplified by breaking down the numbers and calculating individual square roots before multiplying them together.
  • 📈 The area of the triangle is found to be 30 times the square root of 2.
  • 📌 To find the height, use the formula for the area of a triangle (1/2 * base * height) and solve for the height.
  • 📐 The height of the triangle is calculated to be 6 times the square root of 2, which is approximately 8.485 when converted to a decimal.
Q & A

  • What is the main topic of the video?

    -The video discusses how to calculate the height of a triangle when the values of all three sides are known, using Heron's formula.

  • What is Heron's formula used for?

    -Heron's formula is used to calculate the area of a triangle when the lengths of all three sides are known.

  • What is the relationship between the base, height, and area of a triangle?

    -The area of a triangle is equal to one-half the product of its base and height.

  • What is the formula for calculating 's' in Heron's formula?

    -In Heron's formula, 's' is calculated as half the sum of the lengths of all three sides of the triangle (s = (a + b + c) / 2).

  • What are the lengths of the sides used in the example provided in the video?

    -In the example, side 'a' is 9 units, side 'b' is 10 units (the base), and side 'c' is 11 units.

  • How is 's' calculated in the example given?

    -In the example, 's' is calculated as (9 + 10 + 11) / 2, which equals 15.

  • What is the expression for the area of a triangle using Heron's formula?

    -The area of a triangle using Heron's formula is the square root of (s * (s - a) * (s - b) * (s - c)), where s is the semi-perimeter of the triangle.

  • What simplifications were made to calculate the area in the example?

    -The simplifications made include breaking down the numbers 15, 6, 5, and 4 into smaller factors to facilitate easier multiplication and square root calculations.

  • What is the approximate decimal value of the area of the triangle in the example?

    -The approximate decimal value of the area of the triangle is 42.4264 square units.

  • How is the height of the triangle calculated from the area and base?

    -The height of the triangle is calculated by dividing the area of the triangle by the base and then multiplying by 2 (height = (area * 2) / base).

  • What is the exact value and approximate decimal value of the height of the triangle in the example?

    -The exact value of the height is 6 times the square root of 2. The approximate decimal value is approximately 8.485.

  • What is the significance of knowing the area before calculating the height in this method?

    -Knowing the area is significant because it allows you to use the base and area relationship to solve for the unknown height of the triangle.

Outlines
00:00
📏 Calculating Triangle Height Using Heron's Formula

This paragraph introduces the method to calculate the height of a triangle when the lengths of all three sides are known. The process involves using Heron's formula to first determine the area of the triangle. The base of the triangle is given as 10 units, and the other two sides are 9 and 11 units. The semi-perimeter 's' is calculated as half the sum of the sides (a+b+c)/2, which equals 15 in this case. The area is then found using Heron's formula: √[s(s-a)(s-b)(s-c)]. By substituting the values of 's', 'a', 'b', and 'c', the area is simplified to 30√2 square units. To find the height, the formula (Area = 1/2 * base * height) is rearranged to solve for height, resulting in the height being 6√2 units, which is approximately 8.485 when converted to a decimal.

05:00
📐 Summary of Triangle Height Calculation

The second paragraph summarizes the process of calculating the height of a triangle given the lengths of its sides. It emphasizes the use of Heron's formula to find the area of the triangle and then using that area to determine the height. The video concludes with a reminder of the steps involved and thanks the viewer for watching, highlighting the educational value of the content.

Mindmap
Keywords
💡Height of a Triangle
The 'height of a triangle' refers to the perpendicular distance from the base to the opposite vertex. In the context of the video, it is the unknown measurement that the viewer is learning how to calculate using Heron's formula. The script provides a step-by-step guide on how to determine this height when the lengths of all three sides of the triangle are known.
💡Heron's Formula
Heron's formula is a mathematical formula used to calculate the area of a triangle when the lengths of all three sides are known. In the video, it is the primary method used to find the area of the triangle before calculating the height. The formula is introduced as 's times (s - a) times (s - b) times (s - c)', where 's' is the semi-perimeter of the triangle.
💡Area of a Triangle
The 'area of a triangle' is a measure of the space enclosed by the triangle. The script explains that the area can be found using the formula 'one-half base times height'. The concept is central to the video as it is used to find the height once the area is calculated using Heron's formula.
💡Base
The 'base' of a triangle is one of its sides, and it serves as the reference for measuring the height. In the video, the base is given as 10 units long, and it is used in both the area formula and Heron's formula to find the triangle's height.
💡Semi-perimeter (s)
The 'semi-perimeter' (denoted as 's' in the script) is half the perimeter of the triangle, calculated as '(a + b + c) / 2', where 'a', 'b', and 'c' are the lengths of the triangle's sides. It is a crucial value used in Heron's formula to calculate the area of the triangle.
💡Perimeter
The 'perimeter' of a triangle is the total length of its sides. In the video, the perimeter is indirectly used to calculate the semi-perimeter 's', which is then used in Heron's formula. The script mentions the sides of the triangle as 9, 10, and 11, which would sum up to give the perimeter.
💡Square Root
The 'square root' is a mathematical operation that finds the value that, when multiplied by itself, gives the original number. In the script, the square root is used in Heron's formula to calculate the area of the triangle, as the formula involves the square root of certain terms.
💡Decimal Value
A 'decimal value' is a numerical value expressed in decimal form, which includes digits to the right of the decimal point. In the video, the script provides an example of converting the square root of 2 into a decimal value (approximately 1.414213) to calculate a more precise area of the triangle.
💡Exact Value
An 'exact value' refers to the precise numerical value of a quantity without any approximation. The video emphasizes finding the exact value for the area and the height of the triangle. For example, the script mentions that the exact value for the height is '6 times the square root of 2'.
💡Approximation
An 'approximation' is a value that is close to the exact value but is used for convenience or simplicity. In the script, the approximation is used to give a decimal value for the height of the triangle, which is approximately 8.485, making it easier to understand and use in practical applications.
Highlights

The video explains how to calculate the height of a triangle when the lengths of all three sides are known.

Heron's formula is used to calculate the area of the triangle before determining the height.

The formula for the area of a triangle is one-half times the base times the height.

The base of the triangle is given as 10 units.

The sides of the triangle are a=9, b=10, and c=11 units.

The semi-perimeter 's' of the triangle is calculated as (a+b+c)/2.

The value of 's' is calculated to be 15 units.

Heron's formula for the area involves the square root of s(s-a)(s-b)(s-c).

The area calculation simplifies the expression for easier computation.

The area of the triangle is expressed as 30 times the square root of 2.

The decimal approximation of the area is approximately 42.4264 square units.

To find the height, the formula area = (1/2) * base * height is used.

The height of the triangle is calculated to be 6 times the square root of 2.

The decimal approximation of the height is approximately 8.485 units.

The video concludes by summarizing the steps to calculate the height of a triangle using Heron's formula.

The video provides a practical application of Heron's formula for a geometric problem.

Transcripts

Browse More Related Video

How to Find the Area of a Triangle with Trigonometry (Precalculus - Trigonometry 34)

Area of an Oblique Triangle - SAS & SSS - Heron's Formula, Trigonometry

Related Rates - Area of a Triangle

Special Right Triangles - 30 60 90 - Geometry & Trigonometry | SAT Math

Can you find the side lengths of the triangle? | (No Calculators!) |#math #maths #geometry

Math Antics - Area

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Triangle HeightHeron's FormulaArea CalculationMath TutorialGeometry LessonBase Times HeightSides of TriangleCalculus MethodEducational VideoMathematics Help