Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial

The Organic Chemistry Tutor
25 Apr 201710:16
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial offers a clear and concise explanation on how to calculate the determinant of 2x2 and 3x3 matrices. For the 2x2 matrix, the determinant is computed as ad - bc. For the 3x3 matrix, the process involves breaking it down into smaller 2x2 matrices and applying the 2x2 determinant formula iteratively. The video provides step-by-step examples, making it easy for viewers to understand and practice the concept. It also encourages viewers to explore more educational content on various mathematical and scientific topics through the creator's playlists and channel.

Takeaways
  • 📚 The determinant of a 2x2 matrix is calculated as (ad - bc).
  • 🔢 For the example 2x2 matrix with elements 3, -4, 5, 7, the determinant is calculated as (3 * 7) - (5 * -4) = 41.
  • 🔄 To find the determinant of a 3x3 matrix, eliminate the first row and column and apply the 2x2 determinant method to the remaining elements.
  • 🌟 The determinant of a 3x3 matrix is the sum of the products of the elements in the first row and the determinants of the 2x2 matrices formed by the elimination method.
  • 📝 For a 3x3 matrix with elements 2, 4, -3, 5, 7, 68, 1, and 9, the determinant is calculated by (2 * determinant of (7, 68, 1, 9)) - (4 * determinant of (5, 8, 6, 9)) + (-3 * determinant of (5, 7, 4, 9)).
  • 🧩 The determinant of the 3x3 matrix in the example with elements 5, 7, 8, -3, 6, 1, 7, and 9 is -29.
  • 🎓 Understanding matrix determinants is essential for various mathematical and scientific applications, including solving systems of linear equations and finding invertible matrices.
  • 📈 The method for calculating the determinant of a 3x3 matrix can be expanded to larger matrices using similar techniques of elimination and sub-matrix determinants.
  • 🔍 The video script provides a detailed walkthrough with examples, making it an informative resource for learning how to calculate determinants.
  • 👍 The video also encourages viewers to explore more content on related topics such as algebra, trigonometry, pre-calculus, physics, general chemistry, and organic chemistry.
  • 💡 The determinant of a matrix can provide insights into the properties of the matrix, such as whether it is invertible or singular.
Q & A

  • What is the determinant of a 2x2 matrix?

    -The determinant of a 2x2 matrix, given by ad - bc, where a, b, c, and d are the elements of the matrix.

  • How do you calculate the determinant of the 2x2 matrix with elements 35, -47, 7, and -4?

    -You calculate it by multiplying 35 (a) by -4 (d) and subtracting the product of -47 (b) and 7 (c). So, 35*(-4) - (-47)*7 equals 140 - 329, which gives you -189.

  • What is the rule for finding the determinant of a 3x3 matrix?

    -The determinant of a 3x3 matrix is found by a more complex process involving the elimination of the first row and column and then calculating the determinants of smaller 2x2 matrices formed by the remaining elements, summing them up with alternating signs.

  • How do you simplify a 3x3 matrix into 3 separate 2x2 matrices?

    -You simplify a 3x3 matrix into 3 separate 2x2 matrices by eliminating the first row and the corresponding column for each element in the first row. This leaves you with three 2x2 matrices, one for each element in the first row (A1, B1, and C1).

  • What is the expanded form of the determinant calculation for a 3x3 matrix?

    -The expanded form involves multiplying each element in the first row by the determinant of the 2x2 matrix formed by eliminating its row and column, and then summing these products with alternating signs.

  • What is the determinant of the 3x3 matrix with elements 2, 4, -3, 5, 7, 68, 1, and 9?

    -The determinant is calculated as follows: (2 * determinant of the 2x2 matrix formed by eliminating the first row and column) - (4 * determinant of the 2x2 matrix formed by eliminating the first row and second column) + (-3 * determinant of the 2x2 matrix formed by eliminating the first row and third column). After calculating each 2x2 determinant and substituting back, the final determinant is -441.

  • What is the significance of the determinant in linear algebra?

    -The determinant is a scalar value that can provide important information about a matrix. It can be used to determine if a matrix is invertible (non-singular) or not. A non-zero determinant indicates that the matrix has an inverse, while a determinant of zero means the matrix is singular and does not have an inverse.

  • How does the process of calculating the determinant of a 3x3 matrix relate to the concept of expansion by minors?

    -The process of calculating the determinant of a 3x3 matrix is essentially an application of the expansion by minors method. Each element in the first row is multiplied by the determinant of the 2x2 matrix formed by eliminating its row and column, which are essentially the minors of the corresponding elements in the matrix.

  • What are some applications of matrix determinants in real-world scenarios?

    -Matrix determinants have a wide range of applications in various fields. In physics, they can be used to find the volume of transformation in coordinate transformations. In engineering, they can help determine the stability of structures. In statistics, they are used in multivariate analysis, such as in principal component analysis (PCA). They are also used in solving systems of linear equations and in optimization problems.

  • How does the sign pattern in the determinant calculation for a 3x3 matrix affect the final result?

    -The sign pattern, which alternates signs for each term in the determinant calculation formula for a 3x3 matrix, ensures that the contributions from each element in the first row are properly accounted for. Without this pattern, the determinant would not correctly represent the combined effect of the linear transformations represented by the matrix.

  • What happens if all the rows or columns of a matrix are the same?

    -If all the rows or all the columns of a matrix are identical, the determinant will be zero. This is because the off-diagonal elements in the 2x2 matrices formed during the expansion will cancel each other out, leading to a determinant of zero, indicating that the rows (or columns) are linearly dependent.

  • How does the determinant change if you multiply each element in a matrix by a scalar?

    -If you multiply each element in a matrix by a scalar, the determinant of the matrix will be multiplied by the scalar raised to the power of the size of the matrix. For example, if you multiply each element in a 3x3 matrix by a scalar 'k', the determinant will be multiplied by k^3.

Outlines
00:00
📚 Understanding the Determinant of 2x2 and 3x3 Matrices

This paragraph introduces the concept of finding the determinant of 2x2 and 3x3 matrices. It begins by explaining the formula for a 2x2 matrix, which is calculated as (ad - bc). The explanation is supported with examples, such as calculating the determinant of a matrix with elements 3, -4, -3, and 5, resulting in a determinant of 41. The paragraph then transitions into explaining the determinant for a 3x3 matrix, which involves a more complex process of eliminating the first row and column, and then using the remaining elements to form smaller 2x2 matrices. An example is provided, using the matrix 2, 4, -3, 5, 7, 68, 1, and 9, and the process of simplifying and evaluating the determinant is detailed step by step. The paragraph aims to help viewers understand the basic concepts and methods for calculating the determinant of these two types of matrices.

05:01
🔢 Detailed Calculation of 3x3 Matrix Determinant

This paragraph delves deeper into the calculation of the determinant of a 3x3 matrix. It continues from the previous explanation, providing a step-by-step breakdown of the process using a new example matrix: 5, 7, 8, 4, -3, 6, 1, 7, and 9. The explanation involves eliminating the first row and column, and then using the elements to form 2x2 matrices for each element in the first row. Each 2x2 matrix's determinant is calculated and then combined with the appropriate sign (positive or negative) to get the final determinant of the 3x3 matrix. The paragraph concludes with the final determinant calculation, which is -29 for the given example. Additionally, the speaker encourages viewers to explore more videos on related topics such as algebra, trigonometry, pre-calculus, physics, general chemistry, and organic chemistry, and invites them to subscribe to the channel or check out the playlist for more educational content.

Mindmap
Keywords
💡determinant
The determinant is a scalar value that can be computed from the elements of a square matrix and is used to find the invertibility of the matrix. In the context of the video, the method for calculating the determinant of both 2x2 and 3x3 matrices is explained. For a 2x2 matrix, it is computed as the product of the diagonal elements minus the product of the off-diagonal elements. For a 3x3 matrix, the determinant involves more complex operations, breaking down the matrix into smaller 2x2 matrices and applying the rules for 2x2 determinants.
💡2x2 matrix
A 2x2 matrix is a square matrix that has two rows and two columns. It is one of the simplest forms of matrices and is often used to illustrate basic matrix operations such as finding the determinant, matrix multiplication, and systems of linear equations. In the video, the process of finding the determinant of a 2x2 matrix is demonstrated with a clear formula and examples.
💡3x3 matrix
A 3x3 matrix is a square matrix consisting of three rows and three columns. It is more complex than a 2x2 matrix and is used in a variety of mathematical applications, including linear transformations, system of equations, and more. The video explains how to find the determinant of a 3x3 matrix by reducing it to a series of 2x2 matrices and applying the rules for 2x2 determinants.
💡matrix elements
Matrix elements refer to the individual numbers or values that make up the entries of a matrix. Each element is located at a specific position within the matrix, identified by its row and column indices. In the context of the video, understanding and manipulating matrix elements is crucial for calculating the determinant of both 2x2 and 3x3 matrices.
💡diagonal elements
Diagonal elements of a square matrix are those elements where the row index and column index are the same. In a 2x2 matrix, these are the top-left (a) and bottom-right (d) elements. Diagonal elements play a significant role in the calculation of the determinant, especially in smaller matrices where the formula directly involves their product minus the product of the off-diagonal elements.
💡off-diagonal elements
Off-diagonal elements in a square matrix are those elements that are not on the main diagonal. For a 2x2 matrix, these are the top-right (b) and bottom-left (c) elements. These elements are also important in the calculation of the determinant for 2x2 matrices, as they are used in the subtraction part of the determinant formula.
💡submatrices
Submatrices are smaller matrices derived by removing one or more rows and columns from a larger matrix. In the context of calculating the determinant of a 3x3 matrix, submatrices are formed by removing one row and one column at a time, which are then used to calculate the determinant using the method of minors and cofactors.
💡minors
In the context of linear algebra, a minor of a matrix is the determinant of a submatrix formed by removing a row and a column from the original matrix. Minors are used in the process of calculating the determinant of larger matrices, such as 3x3 matrices, by breaking them down into smaller, more manageable 2x2 submatrices.
💡cofactors
Cofactors are related to the concept of minors in linear algebra. The cofactor of an element in a matrix is the determinant of the submatrix from which the element's row and column have been removed, multiplied by (-1)^(i+j), where i and j are the row and column indices of the element, respectively. Cofactors play a crucial role in the expansion of the determinant of a matrix along any row or column.
💡linear algebra
Linear algebra is a branch of mathematics that deals with linear equations, vector spaces, and matrices, among other related concepts. It is a foundational area of study in mathematics with applications in various fields such as physics, computer science, and engineering. The video's content on finding the determinant of matrices is a fundamental topic in linear algebra.
💡invertibility
Invertibility, or the existence of an inverse matrix, is a property of square matrices. A matrix is invertible if there exists another matrix that, when multiplied with the original matrix, results in the identity matrix. The determinant of a matrix is closely related to its invertibility; specifically, a matrix is invertible if and only if its determinant is not zero.
💡systems of linear equations
Systems of linear equations are mathematical representations of multiple linear equations involving the same set of variables. These systems can be represented using matrices and can be solved using various matrix operations, including matrix inversion and determinants. The video's focus on matrices and determinants is directly related to the solution of such systems, as these concepts are often used in their resolution.
Highlights

The method for finding the determinant of a 2x2 matrix is explained.

The determinant of a 2x2 matrix is calculated as (ad - bc).

A practical example is provided to illustrate the calculation of a 2x2 matrix determinant.

The process for finding the determinant of a 3x3 matrix is outlined.

The determinant of a 3x3 matrix involves reducing it to smaller 2x2 matrices and calculating each minor's determinant.

An example is given to demonstrate the calculation of the determinant for a 3x3 matrix with specific numbers.

The video provides a step-by-step breakdown of the calculation process for the 3x3 matrix determinant.

The video also includes another example to reinforce the method of calculating the 3x3 matrix determinant.

The final result of the 3x3 matrix determinant calculation is given as -441.

The video offers additional resources for learning algebra, trigonometry, pre-calculus, physics, general chemistry, and organic chemistry.

The presenter encourages viewers to subscribe to the channel for more educational content.

The video concludes with a thank you message and well wishes for the viewers.

The video is part of a series covering various topics in mathematics and science.

The presenter uses clear and concise language to explain complex mathematical concepts.

The video is designed to be an educational resource for those needing help in specific subject areas.

The video provides a comprehensive guide to matrix determinants, suitable for learners at various levels.

The video emphasizes the importance of practice in understanding and applying the concepts of matrix determinants.

The video's approach to teaching is interactive, encouraging viewers to participate by pausing and working through examples.

Transcripts

Browse More Related Video

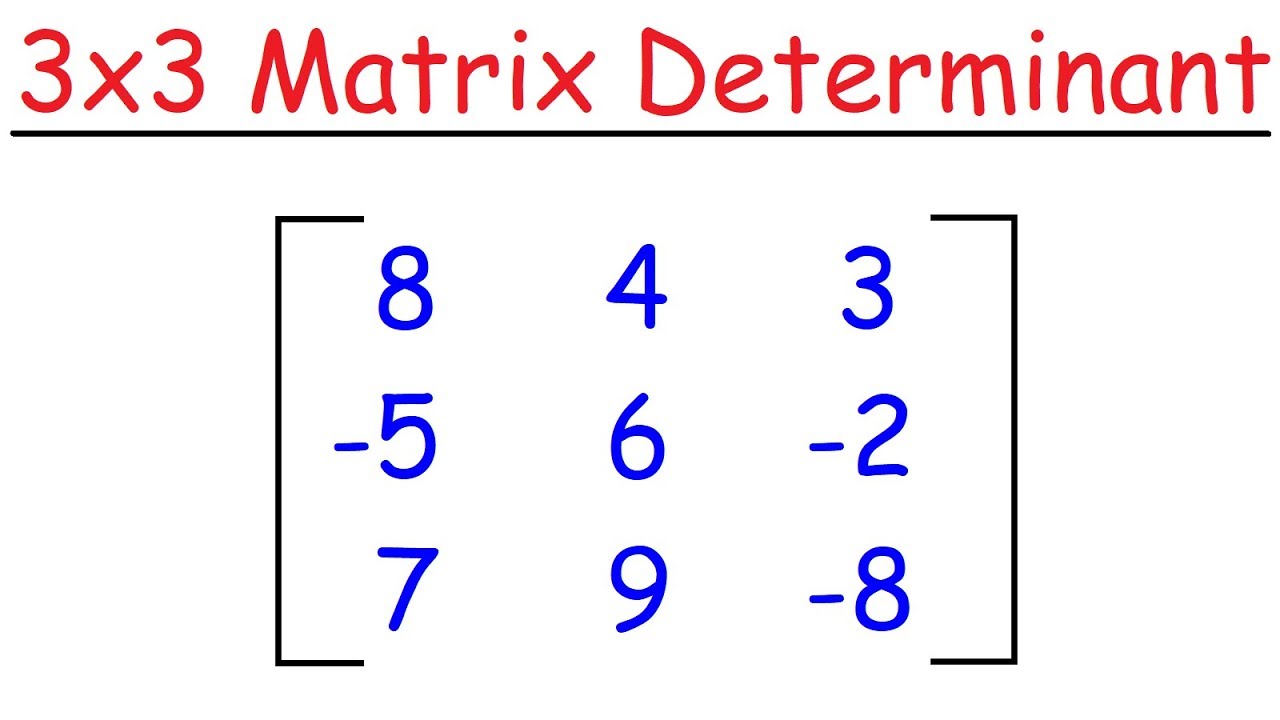
How To Find The Determinant of a 3x3 Matrix

PreCalculus - Matrices & Matrix Applications (30 of 33) Find the Determinant of a 3x3 Matrix 1

How to find the Inverse of a Matrix

How to Invert Matrices - Exercises (Step by Step)

Inverse of a 3x3 Matrix | Co-factor Method

Inverse of a 3x3 Matrix - (THE SIMPLE WAY)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Matrix DeterminantsMathematics TutorialLinear AlgebraEducational VideoAlgebra TechniquesTrigonometry BasicsPre-Calculus ConceptsPhysics ApplicationsChemistry MathOnline Learning