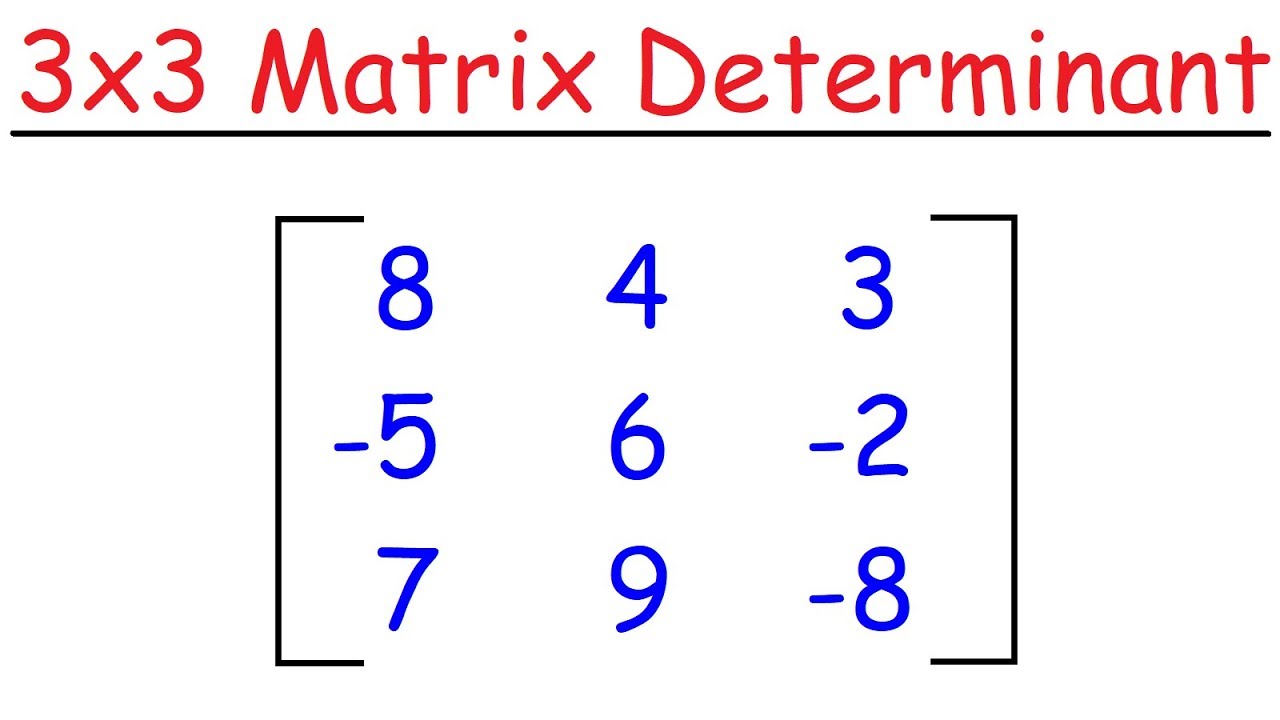
PreCalculus - Matrices & Matrix Applications (30 of 33) Find the Determinant of a 3x3 Matrix 1

Michel van Biezen

19 Jul 201505:01

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial demonstrates the process of finding the determinant of a 3x3 matrix using method one, which involves breaking the matrix into three 2x2 matrices and calculating their determinants with alternating signs. The method is explained step-by-step, with clear instructions on how to cross out rows and columns to simplify the calculation. The final result is obtained by performing arithmetic operations on the determinants of the smaller matrices, ultimately providing the determinant of the original 3x3 matrix. The video also promises to introduce method two in the next episode, suggesting that both methods will yield the same result.

Takeaways

📌 The process involves finding the determinant of a 3x3 matrix using two different methods.
🔢 Method one breaks down the 3x3 matrix into three 2x2 matrices.
🌟 The first step in method one is to assign alternating signs (+, -, +) to the elements of the top row of the 3x3 matrix.
🈹 It involves blocking out certain rows and columns to create the 2x2 matrices.
🧩 The determinant of the 3x3 matrix is calculated as the sum of the products of the elements in the top row and the determinants of the corresponding 2x2 matrices.
➗ Each 2x2 matrix is obtained by crossing out the row and column of the respective element in the top row.
🔄 The signs alternate in a pattern of +, -, + when multiplying the elements by the determinants of the 2x2 matrices.
📊 The final step is to perform the arithmetic by adding and subtracting the products to find the determinant of the original 3x3 matrix.
📈 An example is worked out in the script, resulting in a determinant of -45 for the given 3x3 matrix.
📝 The method is demonstrated in a step-by-step manner, making it easier to understand and follow.
🔜 Method two will be explained in the next video, with the expectation of obtaining the same result as method one.

Q & A

What is the topic of the video?
-The topic of the video is finding the determinant of a 3x3 matrix using method one.
How many methods are mentioned for finding the determinant of a 3x3 matrix?
-Two methods are mentioned for finding the determinant of a 3x3 matrix.
What is the initial step in method one for finding the determinant?
-The initial step in method one is breaking up the 3x3 matrix into three 2x2 matrices.
How are the elements of the top row of the 3x3 matrix treated in method one?
-The elements of the top row are assigned alternating signs: the first is positive, the next is negative, and the third is positive again.
What does the determinant of 'a' represent in the method one explanation?
-The determinant of 'a' represents the result of calculating the determinant of the 2x2 matrix formed by blocking out the row and column of the first element of the 3x3 matrix.
How are the 2x2 matrices formed from the 3x3 matrix in method one?
-The 2x2 matrices are formed by crossing out the respective row and column of the top row elements of the 3x3 matrix.
What is the final expression for calculating the determinant in method one?
-The final expression is 2*(-2) + (-1)*(24) - (-1)*(19) + 3*(8) - (-5)*(-2), which simplifies to -4 + 24 - 19 + 24 - 10, resulting in a determinant of -45.
How does the sign of the top row elements affect the calculation?
-The sign of the top row elements determines the sign of the terms in the final expression for the determinant. If the elements were negative, they would give the opposite sign to the terms.
What is the significance of the alternating signs in the determinant calculation?
-The alternating signs ensure that the determinant calculation correctly accounts for the contributions of each element in the 3x3 matrix when breaking it down into 2x2 matrices.
What will be covered in the next video?
-The next video will show method two for finding the determinant of a 3x3 matrix and will compare the results with method one to ensure they are the same.

Outlines

00:00

📚 Introduction to Finding the Determinant of a 3x3 Matrix

This paragraph introduces the concept of finding the determinant of a 3x3 matrix. It outlines two different methods that can be used to calculate the determinant, with a focus on method one. The explanation begins by breaking down the 3x3 matrix into three 2x2 matrices. It then details the process of assigning positive and negative signs to the elements in the top row of the matrix, which is key to this method. The paragraph goes on to describe the steps of eliminating rows and columns to form smaller matrices and calculating their determinants. The process involves a series of arithmetic operations, including multiplication and subtraction, to arrive at the final determinant value for the 3x3 matrix. The explanation is thorough and provides a clear understanding of the method, ensuring that the viewer can follow along and comprehend the process.

Mindmap

Keywords

💡determinant

The determinant is a scalar value that can be computed from the elements of a square matrix. It is a fundamental concept in linear algebra and has important applications in various fields of mathematics, physics, and engineering. In the context of this video, the determinant of a 3x3 matrix is being calculated using a specific method, which involves breaking down the matrix into smaller 2x2 matrices and applying a rule of signs to the elements of the top row of the original matrix.

💡3x3 matrix

A 3x3 matrix is a rectangular array of numbers with three rows and three columns. It is a type of square matrix, and calculating its determinant involves specific methods and rules. In the video, the process of determining the determinant of a 3x3 matrix is explained step by step, using a combination of arithmetic and linear algebra techniques.

💡linear algebra

Linear algebra is a branch of mathematics that deals with linear equations, vectors, matrices, and their transformations. It is a foundational area of study in mathematics with applications in various scientific and engineering disciplines. The video's main theme revolves around the use of linear algebra techniques to calculate the determinant of a 3x3 matrix, which is a fundamental concept in this field.

💡method one

Method one refers to the specific technique used in the video to calculate the determinant of a 3x3 matrix. This method involves breaking the matrix into three 2x2 matrices, using an alternating sign pattern, and then performing a series of arithmetic operations to arrive at the final determinant value. It is one of the two methods mentioned in the video for finding the determinant of a 3x3 matrix.

💡2x2 matrices

A 2x2 matrix is a small square matrix consisting of two rows and two columns. It is simpler to work with than larger matrices and is often used as a building block in the study of larger matrix systems. In the video, the 3x3 matrix is decomposed into three 2x2 matrices to facilitate the calculation of the determinant using method one.

💡alternating sign

Alternating sign is a pattern where signs change from positive to negative and vice versa in a regular sequence. In the context of the video, the top row elements of the 3x3 matrix are assigned alternating signs (positive, negative, positive) to calculate the determinant using method one. This pattern is crucial for the correct application of the rule and the final calculation of the determinant.

💡arithmetic operations

Arithmetic operations are the basic mathematical processes of addition, subtraction, multiplication, and division. In the video, these operations are used to calculate the determinant of the 3x3 matrix after it has been broken down into 2x2 matrices. The arithmetic operations involve multiplying and subtracting the elements of these matrices according to the rules of method one.

💡crossing out

Crossing out, in the context of the video, refers to the process of eliminating certain rows and columns from the matrix to create smaller 2x2 matrices. This is a step in the method one technique for calculating the determinant of a 3x3 matrix, where specific rows and columns are blocked out to facilitate the computation.

💡sign rule

The sign rule is a method used in mathematics to determine the correct sign for each term in a determinant expansion. In the video, the sign rule is applied to the top row elements of the 3x3 matrix, starting with a positive sign, followed by a negative sign, and ending with a positive sign. This rule is essential for the accurate computation of the determinant using method one.

💡block matrix

A block matrix is a matrix that is partitioned into smaller submatrices, or blocks. In the video, the concept of a block matrix is used to describe the process of isolating certain elements of the 3x3 matrix to form 2x2 matrices. These blocks are then used to calculate the determinant using method one.

💡video tutorial

A video tutorial is an instructional video that provides step-by-step guidance on how to perform a specific task or understand a particular concept. In this case, the video tutorial is focused on teaching the viewer how to calculate the determinant of a 3x3 matrix using two different methods. The video is structured to explain the process clearly and concisely, with the aim of helping the viewer grasp the mathematical concepts involved.

Highlights

Introduction to finding the determinant of a 3x3 matrix

Two different methods for finding the determinant, with a focus on method one

Method one involves breaking up the 3x3 matrix into three 2x2 matrices

The top row elements are assigned with alternating signs: positive, negative, positive

Calculation of the determinant involves multiplying the top row elements by the determinants of the corresponding 2x2 matrices

The determinant of the 3x3 matrix is the sum of the products of the top row elements and their respective 2x2 matrices, with alternating signs

Example calculation: -2 times the determinant of a 2x2 matrix formed by blocking out the first column and row

Mistake correction during the explanation: a plus sign instead of a minus

Final calculation involves simplifying the sum of products and differences of the 2x2 matrices

Result of the determinant calculation: -45

Quick summary of the method for finding the determinant of a 3x3 matrix

The process of selecting the top three elements and assigning them alternating signs

Crossing out specific columns and rows to form 2x2 matrices for calculation

Finding the determinant of the 2x2 matrices by multiplication and sign alternation

Arithmetic to arrive at the final answer for the 3x3 matrix determinant

预告下一视频将展示第二种方法计算3x3矩阵的行列式

Transcripts

Browse More Related Video

How To Find The Determinant of a 3x3 Matrix

Inverse of a 3x3 Matrix | Co-factor Method

How to Invert Matrices - Exercises (Step by Step)

Evaluating the Determinant of a Matrix

How to find the Inverse of a Matrix

Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial

PreCalculus - Matrices & Matrix Applications (30 of 33) Find the Determinant of a 3x3 Matrix 1

Takeaways

Q & A

What is the topic of the video?

How many methods are mentioned for finding the determinant of a 3x3 matrix?

What is the initial step in method one for finding the determinant?

How are the elements of the top row of the 3x3 matrix treated in method one?

What does the determinant of 'a' represent in the method one explanation?

How are the 2x2 matrices formed from the 3x3 matrix in method one?

What is the final expression for calculating the determinant in method one?

How does the sign of the top row elements affect the calculation?

What is the significance of the alternating signs in the determinant calculation?

What will be covered in the next video?