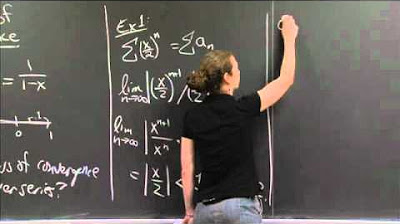ALL OF Calculus 2 in 5 minutes

FuzzyPenguinAMS
7 Dec 202206:09
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a concise introduction to advanced concepts in calculus, focusing on polynomials, transcendental functions, and the approximation of functions through Taylor and Maclaurin series. It delves into the integration of cosine functions and the concept of convergence versus divergence in infinite summations. The importance of understanding intervals of convergence and the application of the ratio test for series convergence is emphasized, providing a solid foundation for further exploration of calculus.

Takeaways
  • 📚 The definition of a polynomial: A function represented by arithmetic operations and powers of 'x' raised to positive integers.
  • 🌟 Examples of valid and invalid polynomials are provided, highlighting the characteristics of polynomial functions.
  • 🔍 Introduction to transcendental functions, which go beyond algebraic expressions and have unique properties.
  • 🧮 The concept of the McLaurin series for approximating transcendental functions like the sine function is discussed.
  • 📈 Explanation of how to use the McLaurin series to approximate the sine function by manipulating derivatives and factorials.
  • 🚀 Demonstration of the approximation process, showing how the function emerges as terms are added and zeros are omitted.
  • 🧩 The Taylor series for cosine function is applied to integrate functions like cos(x^2) by replacing 'x' with 'x^2' and adding '1'.
  • 🤔 Discussion on the integrability of functions and the method to find the integral of non-elementary functions using series expansions.
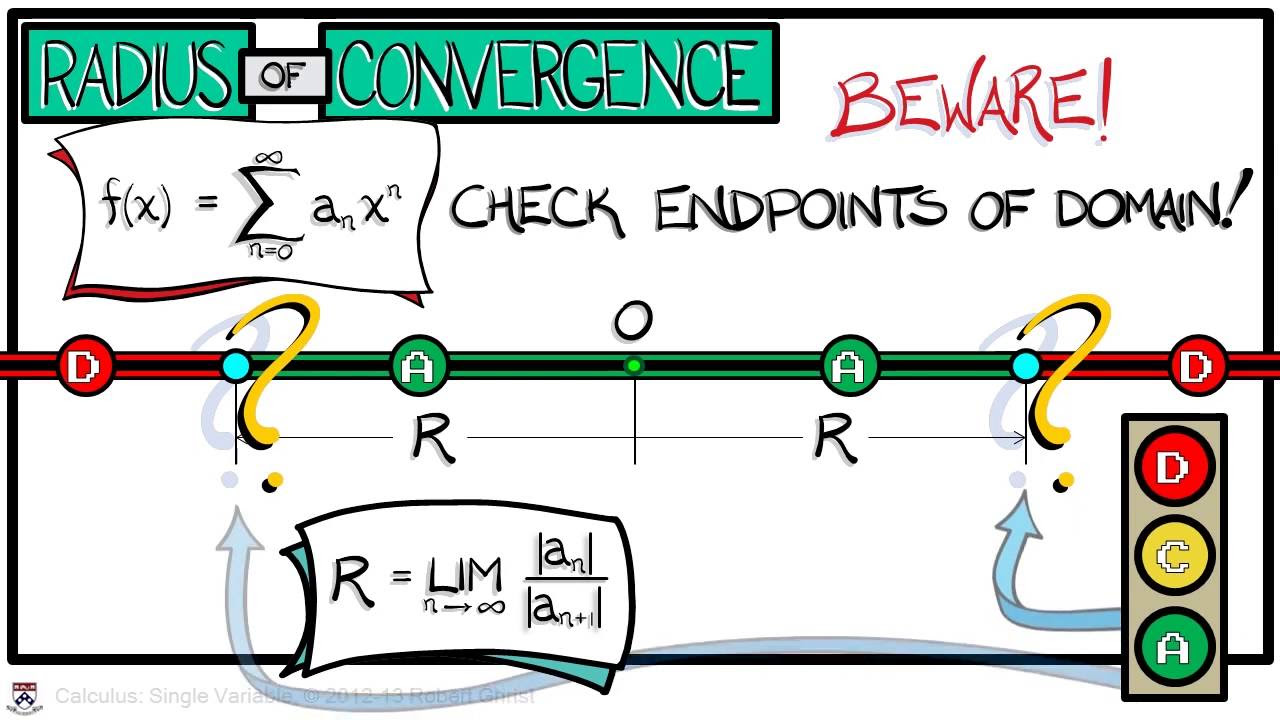
  • 🌐 Understanding convergence versus divergence in summations that extend to infinity, and the conditions that determine these outcomes.
  • 📊 Examination of the interval of convergence for the McLaurin series and the criteria under which the series converges for a given 'x'.
  • 📈 The application of the ratio test to determine the convergence or divergence of a series, with a focus on the behavior of the terms as 'n' approaches infinity.
Q & A

  • What is a polynomial according to the script?

    -A polynomial is a function that can be represented using only arithmetic and x raised to the power of a positive integer.

  • What distinguishes algebraic equations from polynomials?

    -Algebraic equations are not exactly polynomials but are more general mathematical expressions that can involve polynomials as a subset.

  • What are transcendental functions in the context of the script?

    -Transcendental functions are special functions that go beyond algebra, meaning they cannot be expressed algebraically using polynomials and other usual algebraic operations.

  • How does the McLaurin series approximate transcendental functions?

    -The McLaurin series approximates transcendental functions by raising x to various powers, dividing by the corresponding factorials, and summing these terms to create an approximation of the function's value.

  • What is the significance of zeros in the McLaurin series approximation?

    -Zeros in the McLaurin series approximation simplify the expression by eliminating terms, which allows for a more efficient calculation of the function's value as more terms are added.

  • How does the script suggest solving the integral of cosine of x squared?

    -The script suggests using the Taylor series for the cosine function, replacing x with x squared, simplifying the expression, and then adding one to account for the integral, followed by including the constant 'plus C'.

  • What is the importance of the interval of convergence in the context of series?

    -The interval of convergence is crucial as it defines the range of values for the variable (in this case, x) for which the series converges to a single finite sum. Outside of this interval, the series may diverge.

  • How does the script describe the divergence of a series with a power of three?

    -The script indicates that a series with a power of three will diverge because three is outside the range of -1 and 1, which are the typical bounds within which a series may converge.

  • What is the ratio test mentioned in the script, and how is it used?

    -The ratio test is a method to determine the convergence or divergence of an infinite series. It involves dividing the (n+1)th term by the nth term. If the limit of this ratio as n approaches infinity is less than 1, the series converges; if greater than 1, it diverges; if equal to 1, the test is inconclusive.

  • What does the script imply about the limitations of the McLaurin series?

    -The script implies that the McLaurin series cannot approximate every function. There are certain functions and scenarios where the McLaurin series does not converge, highlighting the need for other methods of approximation or analysis.

  • What is the significance of the alternating plus and minus signs in the McLaurin series?

    -The alternating plus and minus signs in the McLaurin series contribute to the series' ability to approximate the value of the function more accurately. This pattern of alternation helps in reducing the error as more terms are added to the series.

Outlines
00:00
📚 Introduction to Polynominals and Transcendental Functions

This paragraph introduces the concept of polynomials, which are functions expressible using arithmetic, x raised to the power of a positive integer, and provides examples of valid and invalid polynomials. It also touches on algebraic equations and transcendental functions, which are special functions that go beyond algebra. The paragraph then delves into how computers calculate transcendental functions using the McLaurin series and approximation, explaining the process of estimating the sign function through the series. It highlights the alternating pattern of plus and minus due to the power of -1 raised to the power of n. The audience is encouraged to solve equations and memorize the formulas for their importance.

05:00
🧮 Special Integrals and Taylor Series

This paragraph discusses the concept of integratable functions and challenges the audience to integrate a specific function, cosine x squared. It introduces the Taylor series for the cosine function and explains how to apply it to integrate the function by replacing x with x squared and adding one. The integral is then found, and the importance of the plus C is emphasized. The paragraph moves on to discuss the concept of convergence versus divergence in summations that extend to infinity, explaining the relationship between variables and how certain values of R indicate convergence or divergence. It concludes with an exploration of the interval of convergence for the McLaurin series and the criteria under which the function converges when X meets specific conditions.

📈 Analyzing Convergence and Divergence with Series

This paragraph focuses on the analysis of convergence and divergence in series. It presents an example of a polynomial and discusses its convergence using the McLaurin approximation and graphical representation. The criteria for the polynomial to satisfy convergence are also discussed. The paragraph then introduces the ratio test as a method to determine if a series converges or diverges. It explains the process of applying the ratio test by examining the value of (n+1)/n and how it leads to convergence when the value approaches zero. The importance of understanding these concepts for solving mathematical problems is emphasized.

Mindmap
Keywords
💡Calculus 2
Calculus 2 is an advanced branch of mathematics that focuses on the study of derivatives and integrals, and their applications. It builds upon the concepts learned in Calculus 1, introducing more complex functions and techniques. In the video, the subject of Calculus 2 is introduced as the main theme, with various topics such as polynomials, transcendental functions, and series being discussed to deepen the understanding of the subject.
💡Polynomials
Polynomials are mathematical expressions consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. They are fundamental in algebra and are used to model a wide range of phenomena in mathematics and science. In the video, polynomials are introduced as functions that can be represented using arithmetic and variable raised to a positive integer power.
💡Transcendental Functions
Transcendental functions are mathematical functions that cannot be expressed as roots or ratios of polynomials. They transcend the boundaries of algebraic expressions and are considered more complex than algebraic functions. Examples include trigonometric functions, exponential functions, and logarithmic functions. In the video, transcendental functions are mentioned as special functions that go beyond algebra, with the concept of approximation using series being discussed.
💡McLaurin Series
The McLaurin series, a specific case of the Taylor series, is a way to approximate functions around a point by expanding them into an infinite sum of terms calculated from the function's derivatives at that point. It is particularly useful for functions that are easier to differentiate and work with than their original form. In the video, the McLaurin series is used to approximate the sign function and other functions, demonstrating how it works by incrementally adding terms to the series.
💡Integration
Integration is a fundamental operation in calculus that involves finding the anti-derivative of a function, which gives the function whose derivative is the original function. It is used to find areas under curves, volumes of solid shapes, and to solve various problems in physics and engineering. In the video, integration is discussed in the context of special integrals, such as integrating cosine of x squared.
💡Convergence
Convergence in mathematics refers to the process of a sequence or series approaching a particular value as the number of terms increases indefinitely. A series or sequence is said to converge if it approaches a finite value; otherwise, it is considered to diverge. In the video, convergence is a key concept in discussing summations that extend to infinity, with the interval of convergence and the ratio test being introduced as methods to determine if a series converges or diverges.
💡Interval of Convergence
The interval of convergence is the set of values for the variable in a power series within which the series converges to a single value. This interval is crucial for determining the domain in which the power series can be used to approximate functions. In the video, the interval of convergence is explained as the range of values for x that satisfy certain criteria, ensuring the convergence of the McLaurin series.
💡Divergence
Divergence in the context of series and sequences refers to the situation where the terms do not approach a finite value as the number of terms increases. A divergent series does not have a sum, and its partial sums continue to increase without bound. In the video, divergence is discussed as the opposite of convergence, with examples illustrating when a summation does not converge to a finite value.
💡Ratio Test
The ratio test is a method used to determine the convergence or divergence of an infinite series. It involves comparing the ratio of consecutive terms as the series progresses. If the limit of this ratio approaches a value less than 1, the series converges; if it approaches a value greater than 1 or diverges to infinity, the series diverges. In the video, the ratio test is introduced as a technique to assess the convergence of a series.
💡Taylor Series
The Taylor series is a representation of a function as an infinite sum of terms calculated from its derivatives at a single point. It is a powerful tool in calculus for approximating functions and solving problems that are difficult to handle with explicit formulas. In the video, the Taylor series is used to approximate the cosine function and to find the integral of 'cosine x^2'.
Highlights

Introduction to Polynominals, which are functions represented using arithmetic and x raised to the power of a positive integer.

Examples of valid and invalid polynomials, emphasizing that all valid polynomials are x raised to a positive integer.

Differentiation between algebraic equations that are not exactly polynomials and transcendental functions, which go beyond algebra.

Explanation of how computers calculate transcendental functions using the McLaren series and approximation.

The process of estimating the sign function using the McLaren series, including the use of zero factorial and derivatives.

Demonstration of the McLaren series approximation in action, showing how the function emerges as terms are added and zeros are omitted.

The alternating pattern of plus and minus signs in the McLaren series, which is determined by -1 raised to the power of n.

Integration of functions, specifically how to integrate cosine x^2 using the Taylor series for cosine of x and the integral operation.

Discussion on the integrability of all functions and the process of solving integrals, including the importance of the plus C in the final answer.

Introduction to the topic of convergence versus divergence in summations that extend to infinity, and the relationship between variables.

Explanation of how to determine if a summation converges or diverges, using the criteria of R being between -1 and 1.

Illustration of the sum of a series and the concept of convergence meaning it equates to a single finite sum.

Discussion on the interval of convergence for the McLaren series and the criteria under which the function converges, including graphical representation.

Comparison of the McLaren series and its approximation with the actual function, showing that they intersect at a specific point determined by certain criteria.

Introduction to the ratio test as a method to determine if a series converges or diverges by evaluating the ratio of consecutive terms.

Application of the ratio test with the example of n + 1 over n, showing that it converges as the value approaches zero when n tends to infinity.

Transcripts

Browse More Related Video

ALL OF Calculus 2 in a nutshell.

Calculus Chapter 5 Lecture 54 Power Series

Ratio Test -- Radius of Convergence | MIT 18.01SC Single Variable Calculus, Fall 2010

Calculus BC Unit 11 Recap

AP Calculus BC Lesson 10.1

Unit 10 Study Guide - AP Calculus (BC Only)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus 2PolynomialsTranscendental FunctionsTaylor SeriesMcLaurin SeriesSpecial IntegralsConvergenceDivergenceSummationInterval of ConvergenceRatio Test