What are confidence intervals? Actually.

This paragraph introduces the concept of confidence intervals, highlighting their prevalence in statistical analysis and their importance in various fields. The speaker, Justin Zeltser, explains that confidence intervals are used to estimate population parameters such as the mean or proportion based on sample data. The video aims to explore the construction, purpose, and application of confidence intervals, focusing on the foundational concepts of health statistics. The speaker also encourages viewers to explore other videos in the series and engage with the content by liking, subscribing, and other forms of support.

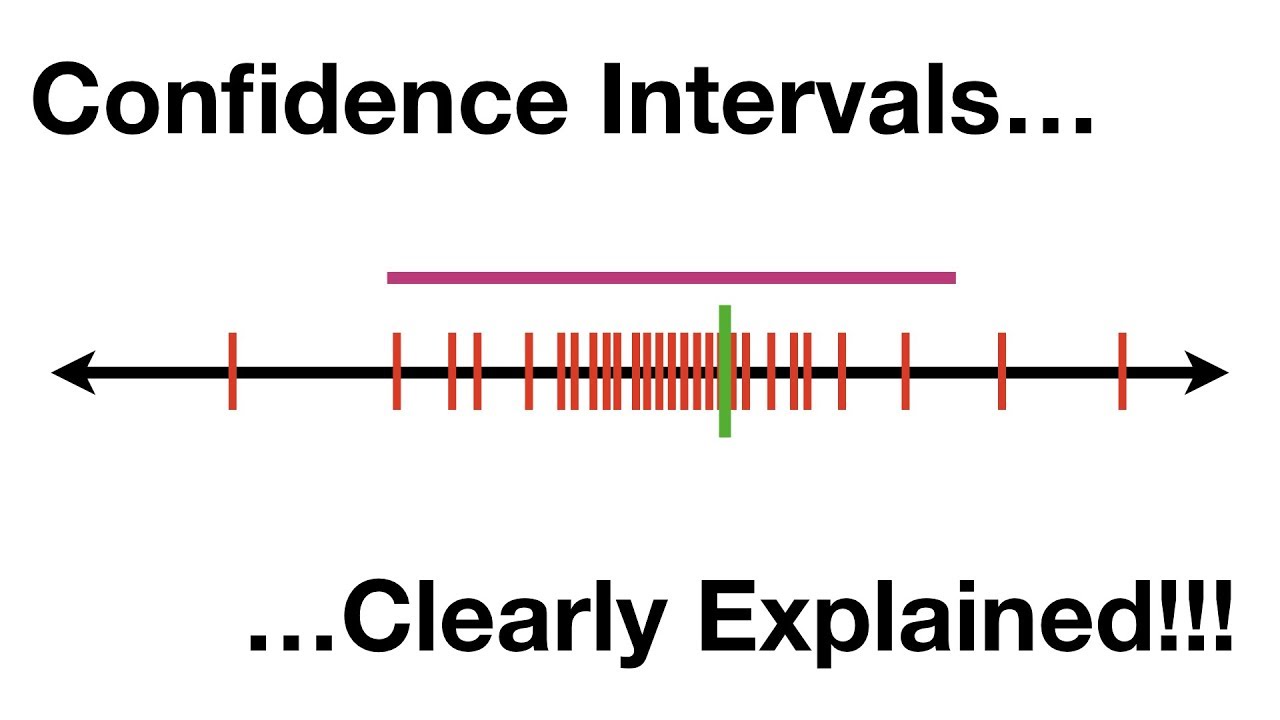
In this paragraph, the speaker works on building the viewer's intuition for confidence intervals without delving into mathematical formulas. An example is used to illustrate the concept of estimating the average resting heart rate for women. The speaker explains that a sample mean is an estimate for the true population mean and that confidence intervals provide a range within which we can be confident the population mean lies. The paragraph emphasizes the idea that statistics is about estimation and that confidence intervals help quantify the uncertainty in our estimates.

This paragraph delves into the actual calculation of confidence intervals for population mean and proportion. The speaker introduces the formulas for constructing these intervals, explaining the components and their significance. The use of sample standard deviation, sample size, and the T distribution for means, as well as the normal distribution for proportions, are discussed. The paragraph also provides an example with 50 women's heart rates, showing how to calculate and interpret the confidence intervals. The speaker emphasizes the relationship between sample size and the width of the confidence interval, and the importance of understanding the T distribution and its role in confidence interval estimation.

The speaker explains how to interpret the calculated confidence intervals, providing a clear understanding of what it means to be 95% confident that a certain range contains the population parameter. Real-world examples from academic papers are used to illustrate the application of confidence intervals in research findings. The paragraph covers different ways confidence intervals can be presented in text, forest plots, and other graphical forms. The speaker also discusses the implications of these intervals in understanding the significance of findings, such as differences in heart rate between various demographic groups.

In the final paragraph, the speaker briefly touches on the difference between frequentist and Bayesian intervals, providing a basic overview of the two statistical approaches. The paragraph explains that frequentists view the parameter as fixed and the sample as random, leading to confidence intervals that aim to capture the true value a certain percentage of the time. In contrast, Bayesians view the parameter as random and assign a prior distribution to it, resulting in credible intervals that express the probability that the parameter falls within a certain range. The speaker notes that while the intervals may often look the same, there are fundamental philosophical differences between the two approaches, and a more in-depth exploration of these differences is available in another video.